 |
Главная |
Энергия магнитного поля. Магнитное поле обладает энергией
|
из
5.00
|
|
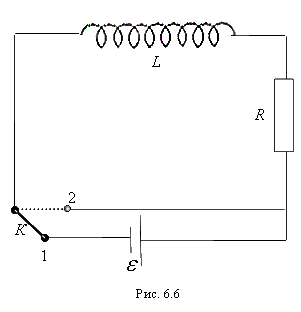
Магнитное поле обладает энергией. Чтобы убедиться в этом, рассмотрим электрическую цепь, содержащую соленоид, имеющий индуктивность  и сопротивление
и сопротивление 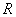 (рис. 6.6). При размыкании ключа К ток не сразу падает до нуля. В течение некоторого времени он продолжает течь, поддерживаемый возникающей в катушке электродвижущей силой самоиндукции, и при этом на сопротивлении выделяется тепло, согласно закону Джоуля–Ленца. Возникает вопрос, за счет каких запасов энергии выделяется тепло, ведь цепь разомкнута, и внешний источник отключен.
(рис. 6.6). При размыкании ключа К ток не сразу падает до нуля. В течение некоторого времени он продолжает течь, поддерживаемый возникающей в катушке электродвижущей силой самоиндукции, и при этом на сопротивлении выделяется тепло, согласно закону Джоуля–Ленца. Возникает вопрос, за счет каких запасов энергии выделяется тепло, ведь цепь разомкнута, и внешний источник отключен.
При уменьшении тока в цепи уменьшается и индукция магнитного поля. Поэтому можно, по-видимому, говорить об энергии электрического тока или энергии магнитного поля, создаваемого током. В случае постоянных токов нельзя однозначно определить, где локализована эта энергия. Ответ на этот вопрос можно дать, изучая переменные магнитные поля или электромагнитные волны. В электромагнитных волнах переменные магнитные поля могут существовать без токов, их поддерживающих. Так как электромагнитные волны переносят энергию, можно заключить, что энергия сосредоточена в магнитном поле.
Найдем величину энергии магнитного поля. Из закона сохранения энергии следует, что, когда ток прекратится, магнитное поле исчезнет, и вся энергия магнитного поля перейдет в тепловую энергию. Согласно закону Джоуля–Ленца, за малое время 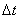 на сопротивлении R выделится количество теплоты
на сопротивлении R выделится количество теплоты 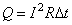 . По закону Ома ток I равен
. По закону Ома ток I равен
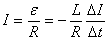 .
.
С учетом этого равенства выделившееся количество теплоты можно записать в виде:
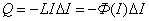 ,
,
|
в этом выражении 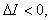 так как ток убывает, а выделяющаяся теплота
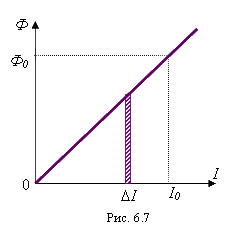
так как ток убывает, а выделяющаяся теплота 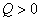 . Зависимость магнитного потока от силы тока можно представить графически (рис. 6.7). Очевидно, что количество теплоты, выделившейся за время
. Зависимость магнитного потока от силы тока можно представить графически (рис. 6.7). Очевидно, что количество теплоты, выделившейся за время 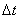 , равно первоначальному запасу магнитной энергии и определяется площадью треугольника, составленного прямой
, равно первоначальному запасу магнитной энергии и определяется площадью треугольника, составленного прямой 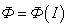 , прямой
, прямой 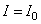 и осью
и осью 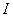 . Эта площадь равна
. Эта площадь равна 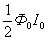 . Таким образом, энергия магнитного поля, создаваемого током I в катушке с индуктивностью L, равна
. Таким образом, энергия магнитного поля, создаваемого током I в катушке с индуктивностью L, равна
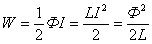 . .
|
Сравните выражение для магнитной энергии, запасенной в катушке индуктивности, с выражением для энергии электрического поля, запасенной в конденсаторе:
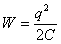 .
.
Энергия электрического поля в конденсаторе пропорциональна квадрату заряда, энергия магнитного поля, запасенная в катушке индуктивности, пропорциональна квадрату силы тока, то есть зависит от скорости движения зарядов. Напомним, что магнитное поле создается движущимися зарядами.
Работа индукционного тока сопровождается нагреванием проводником за счет энергии магнитного поля, которое не может исчезнуть бесследно. Соленоид, таким образом, служит своеобразным резервуаром энергии, значение которой вычисляется по формуле
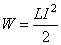 . .
| (6.4) |
Энергию магнитного поля можно выразить через величины, характеризующие само поле. Сделаем это для магнитного поля, создаваемого током в длинном соленоиде. В этом случае 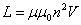 ,
,  , то есть
, то есть 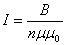 . Подставив эти формулы в (6.4), получим
. Подставив эти формулы в (6.4), получим
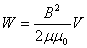 . .
| (6.5) |
Так как магнитное поле внутри соленоида является однородным, то плотность энергии магнитного поля, запасенной в соленоиде, равна энергии, деленной на объем соленоида:
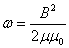 .
.
Пример
Определим энергию магнитного поля соленоида. Обычный лабораторный соленоид длиной 10 см, площадью поперечного сечения 75 см2 и числом витков, намотанных в несколько слоев, равным 3 400, обладает индуктивностью 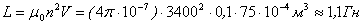 . Сопротивление такого соленоида 50 Ом. При использовании 6-вольтной батарейки установится ток
. Сопротивление такого соленоида 50 Ом. При использовании 6-вольтной батарейки установится ток  . Запасенная в соленоиде магнитная энергия равна
. Запасенная в соленоиде магнитная энергия равна 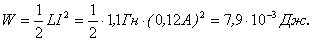 Это небольшая энергия. Однако эта энергия пропорциональна квадрату силы тока и может достигать больших значений. Так, например, в электромагнитах, используемых для исследований, магнитная индукция при максимальном токе составляет обычно от 1 до 1,5 Тл. Магнитная проницаемость железа
Это небольшая энергия. Однако эта энергия пропорциональна квадрату силы тока и может достигать больших значений. Так, например, в электромагнитах, используемых для исследований, магнитная индукция при максимальном токе составляет обычно от 1 до 1,5 Тл. Магнитная проницаемость железа 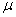 достигает значений в сотни и тысячи единиц, поэтому в электромагните большая часть энергии сосредоточена в зазоре между полюсами электромагнита. Если объем зазора составляет 0,2
достигает значений в сотни и тысячи единиц, поэтому в электромагните большая часть энергии сосредоточена в зазоре между полюсами электромагнита. Если объем зазора составляет 0,2 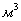 ,то запасенная энергия
,то запасенная энергия
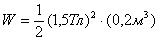 /
/ 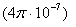 = 1,8
= 1,8 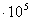 Дж.
Дж.
Это уже немалая энергия! Если, без специальных мер предосторожности, быстро разомкнуть цепь электромагнита, то при 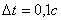 мгновенная мощность составит Р = 1,8 МВт.
мгновенная мощность составит Р = 1,8 МВт.
Взаимная индукция
|
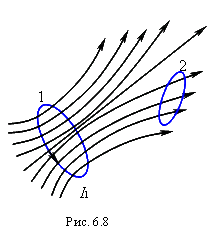
Рассмотрим два неподвижных контура 1 и 2, расположенных достаточно близко друг к другу (рис. 6.8). Будем полагать, что среда является неферромагнитной. Если в контуре 1 течет ток силой, то он создает через контур 2 магнитный поток, пропорциональный 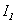 :
:
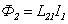 . .
| (6.6) |
Аналогично, если в контуре 2 течет ток силой 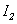 , он создает магнитный поток
, он создает магнитный поток  через контур 1:
через контур 1:
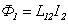 . .
| (6.7) |
Коэффициенты пропорциональности 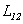 и
и 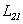 называют взаимной индуктивностью контуров. Из (6.6) и (6.7) видно, что взаимная индуктивность численно равна магнитному потоку через один из контуров при единичном токе в другом контуре. Коэффициенты
называют взаимной индуктивностью контуров. Из (6.6) и (6.7) видно, что взаимная индуктивность численно равна магнитному потоку через один из контуров при единичном токе в другом контуре. Коэффициенты 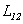 и
и 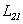 зависят от формы, размеров, взаимного расположения контуров, а также от магнитных свойств среды, окружающей контуры.
зависят от формы, размеров, взаимного расположения контуров, а также от магнитных свойств среды, окружающей контуры.
Можно показать, что при отсутствии ферромагнетиков коэффициенты 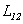 и
и 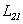 одинаковы:
одинаковы: 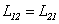 . Это свойство называется теоремой взаимности. Теорема взаимности позволяет не делать различия между
. Это свойство называется теоремой взаимности. Теорема взаимности позволяет не делать различия между 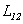 и
и 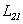 , а говорить просто о взаимной индуктивности двух контуров. Согласно теореме взаимности, если в контурах текут одинаковые токи, то магнитный поток через контур 1, созданный током в контуре 2, равен магнитному потоку через контур 2, созданному током в контуре 1.
, а говорить просто о взаимной индуктивности двух контуров. Согласно теореме взаимности, если в контурах текут одинаковые токи, то магнитный поток через контур 1, созданный током в контуре 2, равен магнитному потоку через контур 2, созданному током в контуре 1.
Если контуры неподвижны и ферромагнетиков вблизи них нет, то при изменении силы тока в одном из контуров в другом контуре возникает электродвижущая сила индукции. Это явление называется явлением взаимной индукции. Согласно закону электромагнитной индукции электродвижущие силы индукции, возникающие в контурах 1 и 2, равны соответственно

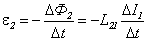 .
.
Если в каком-либо контуре, например, в контуре 1 есть внешний источник электродвижущей силы 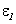 , то с учетом явления самоиндукции полную электродвижущую силу, действующую в этом контуре, можно записать следующим образом:
, то с учетом явления самоиндукции полную электродвижущую силу, действующую в этом контуре, можно записать следующим образом:
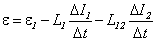 ,
,
где 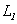 – индуктивность контура 1. Если сопротивление контура 1 равно
– индуктивность контура 1. Если сопротивление контура 1 равно  , то, согласно закону Ома, сила тока в этом контуре будет равна
, то, согласно закону Ома, сила тока в этом контуре будет равна
 .
.
Аналогичное соотношение можно записать и для определения силы тока во втором контуре.
В отличие от индуктивности, которая всегда положительная, взаимная индуктивность величина алгебраическая (в частности, равная нулю). Из рис. 6.8 видно, что знак магнитного потока  при данном направлении тока
при данном направлении тока 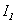 будет зависеть от выбора положительной нормали к поверхности, ограниченной контуром 2. Положительные направления для токов (и электродвижущих сил) в обоих контурах можно выбрать произвольно. При заданном направлении тока направление положительной нормали к поверхности контура определяется правилом правого винта. Если эти направления выбраны, величину
будет зависеть от выбора положительной нормали к поверхности, ограниченной контуром 2. Положительные направления для токов (и электродвижущих сил) в обоих контурах можно выбрать произвольно. При заданном направлении тока направление положительной нормали к поверхности контура определяется правилом правого винта. Если эти направления выбраны, величину 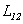 нужно считать положительной, когда при положительных токах магнитные потоки взаимной индукции через контуры оказываются также положительными, то есть совпадают по знаку с потоками самоиндукции.
нужно считать положительной, когда при положительных токах магнитные потоки взаимной индукции через контуры оказываются также положительными, то есть совпадают по знаку с потоками самоиндукции.
Другими словами, 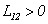 , если при положительных токах в обоих контурах они «подмагничивают» друг друга, в противном случае
, если при положительных токах в обоих контурах они «подмагничивают» друг друга, в противном случае 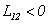 . В частных случаях можно заранее так установить положительные направления обхода контуров, чтобы получить желательный нам знак величины
. В частных случаях можно заранее так установить положительные направления обхода контуров, чтобы получить желательный нам знак величины 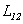 .
.
Пример

|
При отсутствии устойчивого сигнала сотовой связи телефон становится более чувствительным к электромагнитным помехам. Происходит это из-за изменения сигнала вследствие явления взаимоиндукции. Пример такого эффекта – ухудшение приема телефона при приближении к телевизору или радиоприемнику.
6.6. Примеры на применение явления
электромагнитной индукции
|
из
5.00
|
Обсуждение в статье: Энергия магнитного поля. Магнитное поле обладает энергией |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

