ПРОИЗВОДНАЯ СУММЫ, ПРОИЗВЕДЕНИЯ ЧАСТНОГО ДВУХ ФУНКЦИЙ

Для нахождения производных суммы, произведения и частного двух функций используются правила дифференцирования. Рассмотрим и решим примеры.

1. ПРОИЗВОДНАЯ ЛИНЕЙНОЙ ФУНКЦИИL (производная алгебраической суммы):

Производная алгебраической суммы равна алгебраической сумме производных.

2. ПРОИЗВОДНАЯ ПРОИЗВЕДЕНИЯ ДВУХ ФУНКЦИЙ:

Если функции дифференцируемы в точке х₀, то их произведение дифференцируемо в этой точке.

3. ПРОИЗВОДНАЯ ЧАСТНОГО ФУНКЦИЙ:

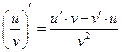
Если функции дифференцируемы в точке х₀,то частное также дифференцируемо в этой точке, если v¹0

ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ (примеры с решениями):

АЛГОРИТМ НАХОЖДЕНИЯ НАИБОЛЬШЕГО И НАИМЕНЬШЕГО ЗНАЧЕНИЙ ФУНКЦИЙ:

АЛГОРИТМ

ПРИМЕР: на отрезке [-3;4]

1. Найти производную функции. 2. Найти критические точки функции (приравняем производную к нулю, и решим полученное уравнения; корни уравнения – критические точки). 3. Вычислить значения функции в критических точках и на концах данного отрезка. 4. Сравнить полученные значения: наибольшее из найденных является наибольшим значением функции на данном отрезке; аналогично – наименьшее является наименьшим на данном отрезке.

Исследовать функцию с помощью первой производной

Обратите внимание, как вариативно можно переформулировать фактически одно и то же задание.

Решение:

1) Функция терпит бесконечные разрывы в точках .

2) Детектируем критические точки. Найдём первую производную и приравняем её к нулю:

Решим уравнение . Дробь равна нулю, когда её числитель равен нулю:

Таким образом, получаем три критические точки:

3) Откладываем на числовой прямой ВСЕ обнаруженные точки и методом интервалов определяем знаки ПРОИЗВОДНОЙ:

Напоминаю, что необходимо взять какую-нибудь точку интервала, вычислить в ней значение производной и определить её знак. Выгоднее даже не считать, а «прикинуть» устно. Возьмём, например, точку , принадлежащую интервалу , и выполним подстановку: .

Два «плюса» и один «минус» дают «минус», поэтому , а значит, производная отрицательна и на всём интервале .

Действие, как вы понимаете, нужно провести для каждого из 6-ти интервалов. Кстати, обратите внимание, что множитель числителя и знаменатель строго положительны для любой точки любого интервала, что существенно облегчает задачу.

Итак, производная сообщила нам, что САМА ФУНКЦИЯ возрастает на и убывает на . Однотипные интервалы удобно скреплять значком объединения .

В точке функция достигает максимума:
В точке функция достигает минимума:

Подумайте, почему можно заново не пересчитывать второе значение.

При переходе через точку производная не меняет знак, поэтому у функции там НЕТ ЭКСТРЕМУМА – она как убывала, так и осталась убывающей.

! Повторим важный момент: точки не считаются критическими – в них функция не определена. Соответственно, здесь экстремумов не может быть в принципе (даже если производная меняет знак).

Ответ: функция возрастает на и убывает на В точке достигается максимум функции: , а в точке – минимум: .

Знание интервалов монотонности и экстремумов вкупе с установленными асимптотами даёт уже очень хорошее представление о внешнем виде графика функции. У графика функции есть две вертикальные асимптоты и наклонная асимптота .
Постарайтесь ещё раз соотнести результаты исследования с графиком данной функции.
В критической точке экстремума нет, но существует перегиб графика (что, как правило, и бывает в похожих случаях).

Найти экстремумы функции:

Решение:

1. Находим производную функции

2. Приравниваем ее к нулю и решаем уравнение

критические точки функции х=1 и х=3.

3. Критические точки функции разбивают область определения на три интервала:

+ - +

1 3 х

определим знаки производной функции в каждом из полученных интервалов:

т.е. точка х=1 – точка максимума; х=3 – точка минимума.

4. Вычислим значения функции в критических точках:

5. Составим таблицу:

Х	(-¥;1)		(1;3)		(3;+¥)
У	+		-		+
У

ИНТЕГРАЛ

Пример 1.

Вычислите определенный интеграл .

Решение.

Пример 2.

Вычислите определенный интеграл .

Решение.

.

Пример 3.

Вычислите определенный интеграл .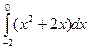

Решение.

.

Пример 4.

Вычислите определенный интеграл .

Решение.

.

Пример 5.

Вычислите определенный интеграл .

Решение.

.