Размеры некоторых объектов, используемых для определения расстояний 7 страница

У таких цилиндрических проекций ли\нией нулевых искажений служит экватор, а изоколы имеют форму г|рямых, параллельных эк­ватору; главные направления совпадают с линиями картографичес­кой сетки, при этом с удалением от экватора искажения увеличи­ваются.

В этих проекциях применяют также проектирование на цилинд­ры сдиаметром меньшим, чем диаметр глобуса, и по-разному отно­сительно глобуса расположенные (рис. 141). В зависимости от ориентировкицилиндра полученные картографические сетки (как и самипроекции) называют нормальными, косыми или поперечными. Нормальные цилиндрические сетки строят на цилиндрах, оси кото-

Г

ЫХ совпадают с осью глобуса (рис. 141, Л и 141,5); косые (рис. 41. в) --на цилиндрах, ось которых составляет с осью глобу-

1*51

са острый угол; поперечные сетки образуются с помощью ци­линдра, ось которого составляет прямой угол с осью глобуса (рис. 141, Г).

В каждом варианте на рисунке 141 изображен общий вид карто­
графической сетки с выделением линии нулевых искажений (ЛНИ).
Нормальная цилиндрическая картографическая сетка на касатель­
ном цилиндре имеет линию нулевых искажений на экваторе. Нор­
мальная сетка на секущем цилиндре имеет две линии нулевых иска­
жений, расположенных вдоль параллелей сечения цилиндра с глобу­
сом (с широтами ф1 и фг). При этом, вследствие сжатия участка
сетки между линиями нулевых искажений, масштабы длин по парал­
лелям оказываются здесь меньше главного; во внешнюю же сторо­
ну от линий нулевых искажений они больше главного масштаба —
как результат растяжения параллелей при проектировании с глобуса
на цилиндр. с "'

Косая цилиндрическая сетка на секущем цилиндре имеет в се­
верной части линию нулевых искажений в\форме прямой, перпен­
дикулярной к среднему меридиану карты и касательной к параллели
с широтой ф; внешний вид сетки представлен кривыми линиями
меридианов и параллелей. _г"~~^

Примером поперечной цилиндрической проекции может служить • проекция Гаусса-Крюгера, в которой каждый поперечно расположен-1 ный цилиндр используется для проектирования поверхности одной зоны Гаусса.

Конические проекции.Для построения картографических сеток в конических проекциях используют нормальные конусы — ка­сательный или секущий (рис. 142).

У всех нормальных конических проекций специфичен внешний вид картографической сетки: меридианы — прямые, сходящиеся в точке, изображающей на плоскости вершину конуса, параллели — дуги концентрических окружностей с центром в точке схода мери­дианов. У сеток, построенных на касательных конусах, одна линия нулевых искажений, с удалением от которой искажения увеличи­ваются (рис. 142 А). Изоколы у них имеют форму дуг окруж­ностей, совпадающих с параллелями.'Сетки, построенные на секу­щем конусе (рис. 142 Б), имеют тот же облик, но иное распределе­ние искажений: линий нулевых искажений у них две. Между ними частные масштабы вдоль параллелей меньше главного, а на внеш­них участках сетки — больше главного масштаба. Главные направле­ния у всех нормальных конических сеток совпадают с меридианами и параллелями.

Азимутальные проекции.Азимутальными называют картографи­ческие сетки, которые получают проектированием фадуснои сетки глобуса на касательную плоскость (рис. 143). Нормальную ази­мутальную сетку получают в результате переноса на плоскость, касательную к глобусу в точке полюса (рис. 143, Л), попереч­ную — при касании плоскости в точке экватора (рис. 143, Б) и ко­сую — при переносе на иначе ориентированную плоскость (рис. 143,5). Внешний вид сеток хорошо виден на рисунке.

f

Рис 142 Распространенные варианты нормальных конических проекции: А -на касательном конусе; Б - на секущем конусе; Р - область растяжении; СЖ -область сжатия. Показана типичная форма изокол

Рис.143. Виды азимутальных проекций: А - нормальная, Б - поперечная,^ В

Косая

S,

Все азимутальные сетки имеют в отношении искажений следу­ющие общие свойства: точкой нулевых искажений (ТНИ) служит точка касания глобуса с плоскостью (обычно она располагайся в центре карты); величины искажений с удалением во все стороны от ТНИ возрастают, поэтому изоколы у азимутальных проекций имеют форму концентрических окружностей с центром в ТНИ

линияГ НяТ^ВЛеНИЯ ^^{еДуЮТ П}° ^РЗДИУ^СУ ^и перпендикулярным им
линиям. Название этой группы проекций связано с тем, что на
картографической сетке, построенной в азимутальной проекции в
бывшей точке касания глобуса и плоскости (т. е. в точке нулевых
искажении) азимуты всех направлений не искажаются ^У

Поликонические проекции. Построение сетки в поликонической проекции можно представить путем проектирования участковгра

"Г п™ ^ГЛ°^буС-^{а На} поверхность нескольких касательных кону­сов и последующей развертки в плоскость образовавшихся на поверхности конусов полос. Общий принцип такого проектирова ния показан на рисунке 144. Буквами на рисунке 144, Л обозначе­ны вершины конусов. На каждый проектируют широтный участок поверхности глобуса, примыкающий к параллели касания соответ ствующего конуса. После развертки конусов получают изображение

Г_РяГ_м^аСТК°^{В В ВИД6 П}°^{Л0С На пл}°™и; полосе соприкасаются по среднему меридиану карты (рис. 144, Б). Окончательный вид сетка

Гн^УиТ^е(^Три^Пс^ОСЛ144^ЛИВ)^{ИАаЦИИ РЭЗРЫВОВ М6ЖДУ П}°^ЛОСаМИ "У^тем Р^астя" Для внешнего облика картографических сеток в полити­ческой проекции характерно, что меридианы имеют форму криви линии (кроме среднего - прямого), а параллели - дуги экцентр" ческих окружностей.^ поликонических проекциях используемых для построения мирокых карт, приэкваториальный участок проек­тируют на касательный цилиндр, поэтому на полученной Тетке ме^Вр^аи^Т_д°и^Ран^И_у^{МееТ Ф}°^{РМУ ПРЯМ}°^{Й ЛИНИ}М перпендикулярной среднему Картографические сетки в поликонических проекциях имеют в приэкваториальных участках масштабы длин близкие к главным ™ным^Мем^РяГ^аНГ ^{И Па}Р^алГ^ей °ни у^Деличены^И%^Иа\нит^ГЛл^аь^Вн^Но^ЬШс

CooTBercZZn⁰^ ^ЧТ° °^СОбеНН° ^{ЗЗМеТН0 В} ^Риферийных частях. Соответственно в этих частях значительно искажены и площади,

пых^У?_и°Г^Нп ^е "^{роекции}- ^К Уловным относят такие проекции, в кото­рых вид получаемых картографических сеток невозможно пред­ставить на основе проектирования на какую-нибудь вспомогатель­ную поверхность. Получают их часто аналитическим путем (на основе решения систем уравнений). Это очень большая группапроек ции^ Из них выделяют по особенностям внешнего вида картографи­ческой сетки псевдоцилиндрические проекции (рис. 145) Как вадно

лели^РИСУпоя^амь1^Пп^ея^{ВДОЦИЛИНДРИЧеСКИХ np}°^eK^ -ватор и^Кп^Вара^Нл° лели — прямые, параллельные друг другу (что полнит _Hv ^ ,„,

₌„_Ческ„_м„ проекциями), V м^дианТ fTx ™кр^.Г

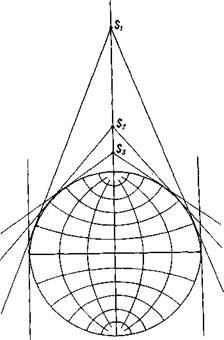
Рис. 144. Принцип построения поликонических проекций

120 80 40

40 80 120 160 160 120 80 40

160 120 80 40 0 40 80 120 160 160 120 80 40

Рис.145. Вид картографической сетки в псевдоцилиндрической проекции

Рис. 147. Центры проектирования в нор­мальных азимутальных проекциях: К\ — центральных, Кг — стереографи­ческих, Къ — внешних, Kt — ортогра-фических

Рис. 146. Вид эллипсов искажений в проекциях равновеликих — А, равноуголь­ных — Б, произвольных — В, в том числе, равнопромежуточных по меридиану — Г и равнопромежуточных по параллели — Д. На схемах показано искажение угла

Классификация картографических проекций по характеру иска­жений.По свойствам изображенной картографической сетки проек­ции делят на равновеликие, равноугольные и произвольные.

г В равновеликих картографических проекциях масштаб площади повсюду имеет одну и ту же величину* Это свойство равновели­ких проекций можно выразить формулой:

P = ax& = Const=l. Неизбежным следствием равновеликости этих проекций являет­ся сильное искажение у них углов и форм, что хорошо поясняют эллипсы искажений (рис. 146, Л).

JB равноугольных проекциях масштабы длин в любой точке по всем направлениям одинаковы, поэтому у них нет искажения фор­мы бесконечно малых фигур и нет искажения углОЦЗ (рис. 146,5). Это общее свойство равноугольных проекций выражает формула ш = 0°. Но формы реальных (конечных) географических объектов, занимающих целые участки на карте, искажаются. У равноуголь­ных проекций наблюдаются особенно большие искажения площадей (что отчетливо демонстрируют эллипсы искажений).

* Произвольными называют картографические проекции с искаже­ниями и углов, и форм, и площадей (рис. 146, В)< Однако величина каждого вида этих искажений обычно не так велика, что у проекций двух предыдущих групп.

#Среди произвольных картографических проекций выделяют группу равнопромежуточных, у которых масштаб длин вдоль одного из главных направлений сохраняется (остается неизменным) (рис.

1 ЛИ ГМ

§ 34. АЗИМУТАЛЬНЫЕ ПРОЕКЦИИ

Общее понятие об азимутальных картографических проекциях и их общих свойствах дано в § 33. Рассмотрим здесь конкретные виды азимутальных проекций с преимущественным вниманием к тем из них, которые используются в учебной картографии. Различают перспективные и неперспективные азимутальные проекции.

Внешний облик картографических сеток и распределение иска­жений в перспективных азимутальных проекциях зависят от поло­жения центра проектирования, т. е. точки пространства, от которой исходят проектирующие лучи. Рассмотрим эти различия на при­мере нормальных картографических сеток (рис. 147). Центр проек­тирования с поверхности шара (глобуса) на касательную плоскость Р может быть расположен в самом центре шара (К\), на его поверх­ности, в точке, противоположной точке касания картинной плос­кости и глобуса (Кг); она может быть также вне шара, на продолже­нии полярной оси глобуса (Кз) и, наконец, на продолжении той же осив бесконечности (К*).

Если точка К расположена в центре шара, проекция называется центральной, а ее нормальная сетка имеет вид, изображенный в ле­вой половине рисунка 148. Хотя на рисунке изображена лишь 1/4 часть получаемой картографической сетки, ее особенности отчетливо видны. По значительному увеличению отрезков меридианов на этой сетке можно заключить, что показатели искажения длин по радиусам (по меридианам) m с удалением от центра сильно возрастают. Не­сколько менее, но так же интенсивно увеличиваются радиусы парал­лелей на проекции, а следовательно, и показатели искажений длин п. Этиискажения влекут за собой иочень большие искажения пло­щадей. В каждой точке карты ш не равно 0°, поэтому и формы ис­кажены. Все эти виды искажения иллюстрируют эллипсы искаже­ний, а по сумме свойств проекцию относят к произвольным.

• Проекция примечательна тем, чтоявляется одной из древней­ших. Впервые ее применил для картызвездного неба в IV в. до н. э. древнегреческий философ Фа-лес. Если с Земли рассматривать небесныйсвод, то кажется, что находишьсяв центре сфериче­ской поверхности, т. е. видишь небесныесветила в центральной

Проекции.

Припроектировании из точки на поверхности шара, противопо­ложной месту касания картинной

&чу/

Рис. 148. Построение и типичный вид нормальных картографических сеток в центральной азимутальной (слева) и азимутальной стереографической (справа) проекциях с эллипсами искажений

плоскости (/С₂), получается стереографическая картографическая сетка (на правой половине рис. 148). По своим свойствам эта сетка равноугольная, а искажения длин и площадей у нее меньше, чем в проекции центральной. В пределах карты полушария в каж­дой точке ш = п, изменяясь от 1 в центре до 2 на краю. Соответ­ственно показатель искажения площадей Р увеличивается в том же направлении от 1 до 4.

На рисунке 149 представлена стереографическая поперечная ази­мутальная картографическая сетка.

В поперечной стереографической сетке меридианы и параллели имеют форму дуг окружностей, а промежутки отрезков экватора и среднего меридиана от центра к краю увеличиваются примерно в два раза. В этой сетке, как и в нормальном варианте, показатели а и b (равные между собой в каждой точке) изменяются от 1 в центре до 2 на краю полушария.

Стереографическая проекция также известна с глубокой древ­ности. Ее разработал астроном Гиппарх во II в. до н. э. С тех пор она применялась широко вплоть до первой четверти нашего сто­летия для карт восточного и западного полушарий.

На рисунке 150 показано проектирование нормальной азимуталь­ной ортографической сетки с центром проектирования Ка, располо­женной бесконечно далеко от шара и картинной плоскости.

Ортографическая картографическая сетка образуется при про­ектировании из бесконечности, когда проектирующие лучи парал­лельны друг другу (и полярной оси глобуса). Как видно на рисун­ке 150 промежутки между параллелями в этой проекции сильно уменьшаются к краю карты полушария. Следовательно, показатели искажения длин по меридианам также в этом направлении уменьша­ются (теоретически они изменяются от 1 в центре до 0 на краю кар­ты) . В то же время радиусы параллелей на проекции равны их радиусам на глобусе, т. е. длина параллелей при проектировании не изменяется и вдоль них нет искажения длин (п=\).

Это значит, что в данной проекции т = 6; п = а; 0<р<1.

РИС.149. Картографическая сетка в азимутальной поперечной стереографической Проекции

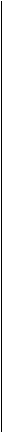
Рис. 150. Построение и типичный вид нормальной картографической сеткив ортографическойазимутальной проек­ции сэллипсами искажений

Проекция имеет искажения углов, которые сильно возрастают к кра­ям карты. По сумме свойств про­екция относится к произвольным, в частности к равнопромежуточ-ным по направлениям, перпенди­кулярным радиусам.

Предложенная еще в Древней Греции (Аполлонием во II в. до н. э.) ортотрафическая проекция широко применяется и ныне в учебной картографии для изобра­жения на картах Земли, рассмат­риваемой как космическое тело, а также для карт Луны и планет Солнечной системы. Это связано с тем, что при фотографировании небесных тел с Земли (или Земли из космического пространства) наблюдатель находится от объек­та на расстоянии, в сто и более раз превышающем его диаметр. Лучи зрения на диаметрально противоположные крайние точки объекта оказываются в этом слу­чае практически параллельными друг другу, а облик объекта или его фотография как бы построен­ными в ортографической проекции.

Чаще других применяются поперечные и косые ортографические
картографические сетки (рис. 151). Так, в географическом атласе
для 5-го класса на схеме, показывающей различия в падении сол­
нечных лучей на земную поверхность, карты земных полушарий
построены в ортографической поперечной проекции; при показе
годового движения Земли вокруг Солнца четыре ее изображения
представлены в косой ортографической проекции. В Географическом
атласе для учителей средней школы эти варианты ортографической
проекции имеют такое же применение. '"'

Из неперспективных азимутальных проекций рассмотрим две/ часто применяемые в учебной картографии,— азимутальную равно! у промежуточную Постеля и азимутальную равновеликую Ламберта]

Азимутальная равнопромежуточная проекция Постеля.Нормаль? ная сетка в этой проекции имеет изображение полюса в центру карты (рис. 152), меридианы у нее прямые, под равными углами, расходящиеся от точки полюса, а параллели — дуги концентри­ческих окружностей с центром в точке полюса. Сетку строят при ' условии, что главный масштаб карты должен сохраняться по всем радиусам, в данном случае — по меридианам. Это условие реали­зуется, если отрезки меридианов между соседними параллелями будут равны и представлять выпрямленные дуги меридианов. Вы-, числение размеров этих отрезков выполняют по формуле:

АА'--

_2л#-Лф "360°-7W

где R — средний радиус Земли (6370 км); Дер — разница широт соседних параллелей, М — знаменатель главного масштаба карты. На рисунке 153 показана поперечная картографическая сетка в азимутальной равнопромежуточной проекции Постеля, а на рисунке 154 — косая сетка в этой же проекции. Все три варианта проек-

 

Рис. 151. Картографическая сетка фическойазимутальной проекции

ая(слева) и косая (справа)в ортогра-

РИС152. Нормальнаякартографическая Рис. 153. Поперечная картографическая
CtTK4 в азимутальнойравнопромежуточной сетка в азимутальной равнопромежу-
,!< |^0*КИИ«1Постеля точной проекции Постеля

| fl 1м. 2М2 Г. Ю. Грюнберг

ции (нормальная, поперечная и ко­сая сетки) имеют общий характер распределения искажений. У всех точка нулевых искажений находится в центре карты. В нормальной про-

)екции она при этом совпадает с изоб­ражением полюса, в поперечной — находится в точке пересечения эква­тора со средним меридианом карты; в косой проекции Постеля (рис. 154) также на среднем меридиане, но в точке, расположенной между эква­тором и полюсом (обычно посереди­не карты).

В этой проекции масштабы длин по радиусам от точки нулевых иска-

Рис. 154. Косая картографическая сетка _жений не изменяются, а ПО НЭПрав-

п_Р0^Г"_еля^{РаВН0ПР0МеЖуТ0ЧН}°^{И лениям}' перпендикулярным радиу-

сам, они возрастают от центра к краям карты полушария примерно в полтора раза. Указанные два на- ^J правления и являются главными, причем по радиусам действует наименьший показатель искажения длин 6 = 1, а по направлениям, перпендикулярным радиусам, действует наибольший показатель а, который изменяется от 1 в центре до 1,57 на краю карты полу­шария.

Если в нормальной сетке главные направления совпадают с линиями картографической сетки (когда а = п, Ь = т), то в двух других вариантах этого совпадения в общем нет. Исключением слу­жит в обоих случаях лишь средний меридиан карты (вдоль него действует показатель Ь), а в поперечной проекции также линия экватора.

Площади и углы в проекции Постеля искажаются. Показатель искажения площадей р = а-Ь изменяется от 1 в центре до 1,57 на краю карты полушария. В общем, азимутальная проекция Постеля относится к произвольным, равнопромежуточным по радиусам из центра карты.

Проекция Постеля была разработана автором в XVI в. Ее при­меняют для построения карт северного (южного) полушария или территорий с меньшим охватом, например карт Арктики и Антарк; тики. В этой проекции в географическом атласе для 7 класса построе­ны карты Антарктиды; в Географическом атласе для учителей сред­ней школы и в Учебном атласе мира (1979 г.) —карты Арктики и Антарктиды. В поперечной проекции Постеля строили в прошлом; карты восточного й западного полушарий.

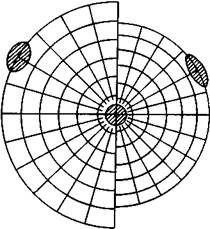
Азимутальная равновеликая проекция Ламберта. Построение азимутальной проекции Ламберта подчинено условию равновели-кости: по всей ее площади должно быть сохранено условие р = а-Ь = =const=1.

Способ достижения этого усло­вия можно понять из сравнения нормальных картографических се­ток, построенных в проекциях Постеля и Ламберта (рис. 155). Вспомним, что благодаря равен­ству отрезков меридианов между параллелями в проекции Постеля и сохранению на меридианах глав­ного масштаба показатель иска­жения длин по этим главным на­правлениям равен 1. По второму же главному направлению пока­затель а больше 1, что влечет уве­личение показателя искажения площади к периферии карты.

Рис. 155. Сравнение форм картографи­ческих сеток в азимутальных проекциях Постеля (слева) и Ламберта (справа)

Чтобы избежать этого и чтобы показатель р = а-Ь оставался всю­ду равным единице, в каждой точ­ке карты увеличение одного со­множителя (а) компенсировалось уменьшением второго сомножителя (Ь). Но это возможно лишь при условии, что отрезки меридианов между параллелями у нормальной сетки не остаются равными (как в проекции Постеля), а умень­шаются к периферии. Это и осуществлено при построении проекции Ламберта. В результате оказалось выполненным условие равно-великости.

Покажем остальные свойства проекции Ламберта примени­тельно к трем вариантам картографической сетки: нормальному, поперечному и косому (рис. 156).

Картографические сетки в азимутальной равновеликой проекции Ламберта: мальная, Б — поперечная, В — косая. ТНИ — точка нулевых искажений

Во всех трех вариантах точка нулевых искажений находится в центре картографической сетки. Показатели искажения длин по направлениям радиусов от этой точки изменяются от 1 до 0,7 на краю карты полушария. По направлениям, перпендикулярным ради­усам, показатель искажения длин а изменяется от 1 в центре до

0 30 6090 120 150

£0____ 60 90 120 150 18

1,4 на краю карты полушария. Углы и формы претерпевают в этой'
проекции значительные искажения, особенно к периферии карты.;
Например, показатель искажения форм на краю карты полушария \
равен 2,0. ,"'

Проекция Ламберта, предложенная автором в XVIII в., имеет и
настоящее время широкое применение. Почти все карты восточного
и западного полушарий, в том числе стенные и настольные, в школь­
ных атласах и учебниках строят в азимутальной поперечной проек- i
ции Ламберта. В этой же проекции строят карты материков: для!
Африки применяют поперечную картографическую сетку в проек­
ции Ламберта, для других материков используют косую картогра- ;
фическую сетку. I

§ 35. ЦИЛИНДРИЧЕСКИЕ ПРОЕКЦИИ

Рассмотрим подробно некоторые из цилиндрических проекций.

Цилиндрическая квадратная проекция на прямом касательном ци­линдре. Проекция неперспективная. При ее построении учи­тывается условие: m = const = 1, т. е. масштабы длин вдоль меридиа­на должны не отличаться от главного. Это условие выполняется при построении сетки прямыми, взаимно перпендикулярными ли­ниями, образующими при пересечении правильные и равные по вели­чине квадраты (рис. 157). Величины отрезков меридианов между соседними параллелями определяются при этом формулой: