 |
Главная |
Электрическое поле заряженной сферы
|
из
5.00
|
Теорема Гаусса.
Потоком вектора напряженности через замкнутый контур площадью S называется произведение проекции вектора напряженности на нормаль к контуру на площадь контура:  .
.
Поток вектора напряженности через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на электрическую постоянную:  .
.
Напряженность поля точечного заряда.
 Для определения напряженности проведем сферическую поверхность S радиусом r с центром совпадающим с зарядом и воспользуемся теоремой Гаусса. Так как внутри указанной области находится только один заряд q, то согласно указанной теореме получим равенство:
Для определения напряженности проведем сферическую поверхность S радиусом r с центром совпадающим с зарядом и воспользуемся теоремой Гаусса. Так как внутри указанной области находится только один заряд q, то согласно указанной теореме получим равенство:  (1), где En - нормальная составляющая напряженности электрического поля. Из соображений симметрии нормальная составляющая должна быть равна самой напряженности и постоянна для всех точек сферической поверхности, поэтому E=En=const. Поэтому ее можно вынести за знак суммы. Тогда равенство (1) примет вид
(1), где En - нормальная составляющая напряженности электрического поля. Из соображений симметрии нормальная составляющая должна быть равна самой напряженности и постоянна для всех точек сферической поверхности, поэтому E=En=const. Поэтому ее можно вынести за знак суммы. Тогда равенство (1) примет вид  , что и было получено из закона Кулона и определения напряженности электрического поля.
, что и было получено из закона Кулона и определения напряженности электрического поля.
Электрическое поле заряженной сферы
 Если сфера проводящая, то весь заряд находится на поверхности. Рассмотрим две области I – внутри сферы радиуса R с зарядом q и вне сферы область II.
Если сфера проводящая, то весь заряд находится на поверхности. Рассмотрим две области I – внутри сферы радиуса R с зарядом q и вне сферы область II.
Для определения напряженности в области I проведем сферическую поверхность S1 радиусом r1 (0<r1<R) и воспользуемся теоремой Гаусса. Так как внутри указанной области зарядов нет, то согласно указанной теореме получим равенство:  (1), где En - нормальная составляющая напряженности электрического поля. Из соображений симметрии нормальная составляющая должна быть равна самой напряженности и постоянна для всех точек сферической поверхности, поэтому E1=En=const. Поэтому ее можно вынести за знак суммы. Тогда равенство (1) примет вид
(1), где En - нормальная составляющая напряженности электрического поля. Из соображений симметрии нормальная составляющая должна быть равна самой напряженности и постоянна для всех точек сферической поверхности, поэтому E1=En=const. Поэтому ее можно вынести за знак суммы. Тогда равенство (1) примет вид  . Т. к. площадь сферы не равна нулю, то Е1=0 (во всех точках области I) – внутри проводника зарядов нет и напряженность поля равна нулю.
. Т. к. площадь сферы не равна нулю, то Е1=0 (во всех точках области I) – внутри проводника зарядов нет и напряженность поля равна нулю.
В области II R£r2 проведем сферическую поверхность S2 радиусом r2 и воспользуемся теоремой Гаусса:
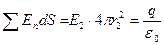 (2), Þ
(2), Þ  - напряженность поля вне сферы рассчитывается по той же формуле, что и напряженность поля точечного заряда.
- напряженность поля вне сферы рассчитывается по той же формуле, что и напряженность поля точечного заряда.
 Электрическое поле заряженного шара
Электрическое поле заряженного шара
Заряд равномерно распределен по всему объему шара, поэтому введем понятие объемной плотности заряда:  . Рассмотрим две области I – внутри сферы радиуса R с зарядом q и вне сферы область II.
. Рассмотрим две области I – внутри сферы радиуса R с зарядом q и вне сферы область II.
Для определения напряженности в области I проведем сферическую поверхность S1 радиусом r1 (0<r1<R) и воспользуемся теоремой Гаусса:  - напряженность поля внутри шара увеличивается прямо пропорционально расстоянию до центра шара.
- напряженность поля внутри шара увеличивается прямо пропорционально расстоянию до центра шара.
В области II R £ r2 проведем сферическую поверхность S2 радиусом r2 и воспользуемся теоремой Гаусса:
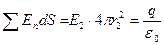 (2), Þ
(2), Þ  - напряженность поля вне шара рассчитывается по той же формуле, что и напряженность поля точечного заряда.
- напряженность поля вне шара рассчитывается по той же формуле, что и напряженность поля точечного заряда.
|
из
5.00
|
Обсуждение в статье: Электрическое поле заряженной сферы |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

