 |
Главная |
Построение моделей временных рядов в соответствии с методологией Бокса-Дженкинса. Модели ARIMA
|
из
5.00
|
Для временного ряда далеко не всегда удается подобрать адекватную модель, для которой ряд возмущений 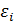 будет удовлетворять основным предпосылкам регрессионного анализа. До сих пор мы рассматривали модели, в которых в качестве регрессора выступала переменная «t» - время. В эконометрике достаточно широкое распространение получили и другие регрессионные модели, в которых регрессорами выступают лаговые переменные, т.е. переменные, влияние которых в эконометрической модели характеризуется некоторым запаздыванием. Еще одним отличием рассматриваемых регрессионных моделей является то, что представленные в них объясняющие переменные являются величинами случайными.
будет удовлетворять основным предпосылкам регрессионного анализа. До сих пор мы рассматривали модели, в которых в качестве регрессора выступала переменная «t» - время. В эконометрике достаточно широкое распространение получили и другие регрессионные модели, в которых регрессорами выступают лаговые переменные, т.е. переменные, влияние которых в эконометрической модели характеризуется некоторым запаздыванием. Еще одним отличием рассматриваемых регрессионных моделей является то, что представленные в них объясняющие переменные являются величинами случайными.
Авторегрессионная модель р-го порядка имеет вид:
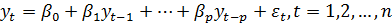 , где
, где 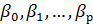 - некоторые константы.
- некоторые константы.
Она описывает изучаемый процесс в момент времени t в зависимости от его значений в предыдущие моменты t-1, t-2, …,t-p.
Если исследуемый процесс 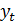 в момент t определяется его значениями только в предшествующий период t-1, то рассматривают авторегрессионную модель 1-го порядка (или модель AR(1) – марковский случайный процесс):
в момент t определяется его значениями только в предшествующий период t-1, то рассматривают авторегрессионную модель 1-го порядка (или модель AR(1) – марковский случайный процесс):
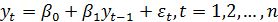
Наряду с авторегрессионными моделями временных рядов в эконометрике рассматриваются также модели скользящей средней (не путать с аналогичным термином при сглаживании временных рядов), в которой моделируемая величина задается линейной функцией от возмущений (ошибок) в предыдущие моменты времени. Модель скользящей средней q-го порядка или модель MA(q) имеет вид: 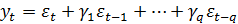
В эконометрике используются также комбинированные модели временных рядов AR и MA – авторегрессионная модель скользящей средней порядков p и q соответственно (или ARMA(p,q)) имеет вид: 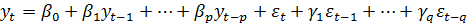 .
.
Использование соответствующих авторегрессионных моделей для прогнозирования экономических показателей, т.е. прогноз на базе рассмотренных моделей, может оказаться весьма эффективным (как правило, в краткосрочной перспективе).
Модель авторегрессии – проинтегрированного скользящего среднего порядка 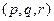 ARIMA(p,q,r)
ARIMA(p,q,r)
Обозначим:
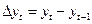 (1)
(1)
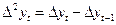 (2)
(2)
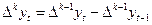 (3)
(3)
Случайная последовательность 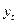 называется рядом ARIMA(p,q,r), если ряд
называется рядом ARIMA(p,q,r), если ряд 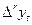 является (стационарным) рядом ARMA(p,q), т.е. ряд
является (стационарным) рядом ARMA(p,q), т.е. ряд 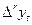 является стационарным (в слабом смысле) и имеет место равенство:
является стационарным (в слабом смысле) и имеет место равенство:
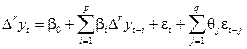 (4)
(4)
где 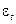 независимые нормально распределенные случайные величины с нулевым математическим ожиданием и постоянной дисперсией
независимые нормально распределенные случайные величины с нулевым математическим ожиданием и постоянной дисперсией 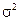 :
:
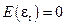 ,
, 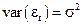 ,
, 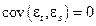 . (5)
. (5)
Оценивание параметров для модели ARIMA(p,q,r) сводится к оценке параметров модели ARMA(p,q) для ряда 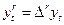 ,
, 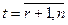
Прогнозирование осуществляется в два этапа.
На первом этапе находятся прогнозные значения 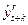 ряда
ряда 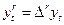 в рамках модели ARMA(p,q).
в рамках модели ARMA(p,q).
Затем находятся прогнозные значения 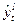 ,
,  для
для 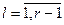 рекуррентным образом (начиная с
рекуррентным образом (начиная с 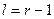 ) по следующим принципам.
) по следующим принципам.
Сначала находится значение 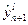 по формуле:
по формуле:
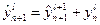 (6)
(6)
Затем рекуррентным образом находятся значения 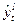 при
при 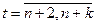 по формуле:
по формуле:
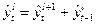 (7)
(7)
После того, как уже найдены значения 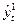 ,
,  , находится значение
, находится значение 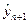 по формуле:
по формуле:
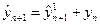 (8)
(8)
Затем рекуррентным образом находятся значения 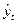 при
при 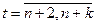 по формуле:
по формуле:
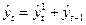 (9)
(9)
Порядок 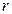 модели ARIMA(p,q,r) – это наименьшее значение
модели ARIMA(p,q,r) – это наименьшее значение 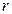 , при котором ряд
, при котором ряд 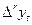 является стационарным.
является стационарным.
Для исследования ряда 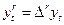 на стационарность используется тест Дики-Фуллера.
на стационарность используется тест Дики-Фуллера.
42 Статическая модель межотраслевого баланса (МОБа). Экономическое содержание разделов таблицы МОБа.
 Стат. межотр. модели испол-ся для разработки планов выпуска и потребления продукции и основываются на соотношениях МОБа. При построении делают предположения: 1) все продукты в отрасли однородны и рассм-ся как целое(1отрасль-1продукт); 2) в каждой отрасли 1 технология производства; 3) нормы производ-ных затрат не зависят от объёма выпуска; 4) не допускается замещение сырья другим. При этих предположениях: xij = aij*xj, где aij- коэфф-т прямых материальных затрат и показывает, какое количество продукции i-й отрасли идет на производство единицы продукции j-й отрасли.
Стат. межотр. модели испол-ся для разработки планов выпуска и потребления продукции и основываются на соотношениях МОБа. При построении делают предположения: 1) все продукты в отрасли однородны и рассм-ся как целое(1отрасль-1продукт); 2) в каждой отрасли 1 технология производства; 3) нормы производ-ных затрат не зависят от объёма выпуска; 4) не допускается замещение сырья другим. При этих предположениях: xij = aij*xj, где aij- коэфф-т прямых материальных затрат и показывает, какое количество продукции i-й отрасли идет на производство единицы продукции j-й отрасли.
Они считаются в модели постоянными. Подставляем в Xi = ∑xij + Yi (из класс. МОБ – 2й квадрант) и в итоге Xi = aij*xij + Yi В матричном виде: X = AX + Y - баланс распределения продукции, где X = (X1,.,Xn) - вектор валовых выпуков; Y = (y1,.,yn) - вектор конечного продукта; A- матрица коэфф-в прямых материальных затрат. Коэфф-ты прям. матер-х затрат явл-ся основн. параметрами стат. межотр. модели. Значения получают: 1) статистически (анализ отчётных балансов за прошлые годы); 2) нормативно (отрасль состоит из производств, для кот. разработаны нормативы затрат; на их основе рассчит. коэфф-ты. Баланс распределения продукции использ. для анализа и план-ния стр-ры экономики. При известных коэфф-тах прям. мат. затрат, можно опред. необход. валовые выпуски отраслей. Преобразуем: X - AX = Y; -> X (E - A) = Y; -> X = (E - A)-1Y, где E - единичная матрица. B = (E - A)-1 - матрица полных матер-х затрат, а bij – коэфф-ты полных матер-х затрат и показ-т, каков должен быть валовый выпуск i-й отрасли для того, чтобы обеспечить выпуск единицы конечного продукта j-й отрасли. Чтобы В существовала, необх-мо: 1. aij ≥ 0 (из неотрицательности xij и положительности Xj); 2.Сумма элем-в матрицы A по столбцу < 1. При выполнении условий А – продуктивна.
Коэфф-ты косвенных затрат порядка (r+1):
Коэфф-ты косвенных затрат порядка r являются элементами матрицы 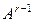 , где (r+1) - показатель степени матрицы для всех целых значений
, где (r+1) - показатель степени матрицы для всех целых значений 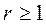 . Коэфф-ты промеж-х затрат сij :
. Коэфф-ты промеж-х затрат сij : 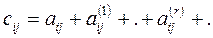 Если aij продуктивна, то бесконечный ряд сходится. В матричной записи справедливо:
Если aij продуктивна, то бесконечный ряд сходится. В матричной записи справедливо: 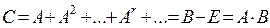 , где С - матрица коэфф-в промежуточных мат затрат. Вывод: Эта Модель – статическая и все зависимости отнесены к 1му моменту врем. Они разрабат-ся для отдел-х периодов, а динамика отображается рядом независимо рассчит-х моделей, что вносит опред. упрощения и сужает возможности анализа.
, где С - матрица коэфф-в промежуточных мат затрат. Вывод: Эта Модель – статическая и все зависимости отнесены к 1му моменту врем. Они разрабат-ся для отдел-х периодов, а динамика отображается рядом независимо рассчит-х моделей, что вносит опред. упрощения и сужает возможности анализа.
Информационной базой модели МОБ выступает отчетный МОБ, который отражает на уровне народного хозяйства производство и распределение валовой продукции в отраслевом разрезе. Модель МОБ – система уравнений, каждое из которых выражает требование баланса в разрезе каждой отрасли между производимым количеством продукции и совокупной потребностью в этой продукции. xij- поставка продукции из i -й отрасли в j-ю отрасль; zij - объем i-го элемента добавленной стоимости в j-й отрасли; Xi- вал. продукция i -й отрасли.
Основой баланса является совокупность всех отраслей материального производства и сферы услуг. На представленной схеме все отрасли агрегированы в три отрасли, каждая из которых в балансе фигурирует дважды: как производящая и как потребляющая. Отрасли как производителю продукции соответствует определенная строка, как потребителю продукции — определенный столбец. Пусть 1я отрасль – это промышленность, 2я – прочие отрасли мат. производства, 3я – отрасли сферы услуг. Столбец (x11, x21, x31) характеризует структуру промежуточных затрат промышленности; а элементы столбца (x11 , x21 ) - структуру материальных затрат промышленности. В столбцах 3го квадранта отражается структура элементов ВДС каждой отрасли. Так, элементы 1го столбца (z11 z21 z31 z41 z51 ) показывают в промышленности потребление осн.капитала, зарплату, прибыль, косв.налоги, субсидии. Сумма всех элементов 1го столбца представляет ВДС промышленности. Элементы 1й строки (z11 z12 z13 ) указ-ют потребление основного капитала в разрезе каждой отрасли, сумма всех элементов 1й строки – ПОК в целом по народному хозяйству.
В столбцах третьего квадранта МОБ отражается структура элементов валовой добавленной стоимости каждой отрасли. Элементы первого столбца (z11, z21, z31, z41, z51)показывают в промышленности потребление основного капитала, заработную плату, прибыль, косвенные налоги, субсидии соответственно (знак «-» в строке «Субсидии» исключает двойной счет при определении валовой добавленной стоимости). Сумма всех элементов первого столбца ( 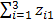 ) представляет валовую добавленную стоимость промышленности. Элементы первой cтроки (z11, z12, z13) указывают потребление основного капитала в разрезе каждой отрасли, сумма всех элементов первой строки (
) представляет валовую добавленную стоимость промышленности. Элементы первой cтроки (z11, z12, z13) указывают потребление основного капитала в разрезе каждой отрасли, сумма всех элементов первой строки ( 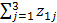 ) — потребление основного капитала по народному хозяйству в целом.
) — потребление основного капитала по народному хозяйству в целом.
1й и 3й квадранты описывают стоимостную структуру валовых затрат (мат.затраты, опл.труда, ПОК, прибыль и.т.д.). В отчетном МОБ окаймляющая строка представляет валовые затраты(ВЗ). Валовой выпуск каждой отрасли должен совпадать с ВЗ. Для любой отрасли-потребителя: 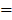
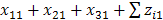 ,
, 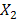 = …,
= …, 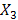 =…(валовые затраты отрасли-потребителя (xj) определяются промеж. затратами ПЗ (
=…(валовые затраты отрасли-потребителя (xj) определяются промеж. затратами ПЗ ( 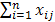 ) и ВДС (zj)).
) и ВДС (zj)).
| Отрасли-производители | Отрасли-потребители | ПП | Конечное использование | Всего | ВВП | ||||
| КП | ВН | ΔЭИ | |||||||
| x11 | x.. | x.. | 𝞢x1j | y11 | y.. | y.. | 𝞢y1j | X1 | |
| x.. | x.. | x.. | 𝞢x2j | y.. | y.. | y.. | 𝞢y2j | X2 | |
| x.. | x.. | x.. | 𝞢x3j | y.. | y.. | y.. | 𝞢y3j | X3 | |
| Промежут. затраты | 𝞢xi1 | 𝞢xi2 | 𝞢xi3 | 𝞢𝞢xij | 𝞢yi1 | 𝞢yi2 | 𝞢yi3 | 𝞢𝞢yij | 𝞢Xj |
| Потребл. осн. капитала | z11 | z12 | z13 | 𝞢z1j | |||||
| Зарплата | Z21 | Z.. | Z.. | 𝞢Z3j | КП – конечное потребление ВН – валовое накопление ΔЭИ – чистое сальдо экспорта-импорта | ||||
| Прибыль | Z31 | Z.. | Z.. | 𝞢Z3j | |||||
| Косвенные налоги | Z41 | Z.. | Z.. | 𝞢Z4j | |||||
| Субсидии | Z51 | Z.. | Z.. | 𝞢Z5j | |||||
| ВДС | 𝞢zi1 | 𝞢zi2 | 𝞢zi3 | 𝞢𝞢zij | |||||
| Валовые затраты | X1 | X2 | X3 | 𝞢Xj |
|
из
5.00
|
Обсуждение в статье: Построение моделей временных рядов в соответствии с методологией Бокса-Дженкинса. Модели ARIMA |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

