Построение кривых линий

В задании строятся коробовые и лекальные кривые линии.

Коробовая линия – выпуклая кривая линия, состоящая из сопряженных дуг окружностей различных радиусов. Наиболее распространенными из них являются овалы.

Лекальные линии – кривые линии, построение которых выполняется по предварительно определенным точкам, например: эллипс, парабола, гипербола.

 

3.1. Построение овала

Овал представляет собой сопряжение двух дуг одного радиуса с двумя дугами другого радиуса.

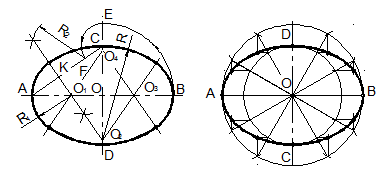
Построение овала по двум осям (рисунок 22) выполняется следующим образом:

- проводят осевые линии, на которых симметрично от точки пересечения O откладывают отрезки AB и CD, равные большой и малой осям овала;

- на малой оси откладывают расстояние OE=OA и соединяют точки A и C;

- на отрезке AC откладывают отрезок CF=CE;

- делят отрезок AF пополам (см. п. 2.1.1) и через точку K проводят прямую перпендикулярную AF до пересечения с большой и малой осями овала в точках O₁ и O₂;

- строят зеркальное отображение точек O₁ и O₂ (точки O₃ и O₄);

- из точек O₂ и O₄ радиусом R= O₂C, а из точек O₁ и O₃ радиусом R₁= O₁A проводят дуги до их пересечения с прямыми, проведенными через центры дуг (точки сопряжения). Существуют и другие способы построения овала.

 

Рисунок 22 – Построе- Рисунок 23 – Построение

ние овала эллипса

 

3.2. Построение эллипса

Эллипс – замкнутая плоская выпуклая кривая, сумма расстояний каждой точки которой до двух данных точек, называемых фокусами, лежащих на большой оси постоянная, и равна длине большой оси. Построение овала по двум осям (рисунок 23) выполняется следующим образом:

- проводят осевые линии, на которых симметрично от точки пересечения O откладывают отрезки AB и CD, равные большой и малой осям эллипса;

- строят две окружности радиусами равными половине осей эллипса с центром в точке пересечения осей;

- делят окружность на двенадцать равных частей. Деление окружности выполняют как показано в п.2.3;

-.через полученные точки проводят лучи-диаметры;

- из точек пересечения лучей с соответствующими окружностями проводят прямые линии параллельно осям эллипса до их взаимного пересечения в точках лежащих на эллипсе;

- полученные точки соединяют плавной кривой линией при помощи лекал. При построении лекальной кривой линии необходимо выбирать и располагать лекало так, чтобы соединялось как минимум четыре-пять точек.

Существуют и другие способы построения эллипса.

 

3.3. Построение параболы

Парабола – плоская кривая линия, каждая точка которой равноудалена от директрисы DD₁– прямой, перпендикулярной к оси симметрии параболы, и от фокуса F, точки расположенной на оси симметрии. Расстояние KF между директрисой и фокусом называется параметром параболы p.

На рисунке 24 показан пример вычерчивания параболы по вершине O, оси OK и хорде CD. Построение выполняют следующим образом:

- проводят горизонтальную прямую линию на которой отмечают вершину O и откладывают ось OK.;

- через точку K проводят перпендикуляр на котором симметрично вверх и вниз откладывают длину хорды параболы;

- строят прямоугольник ABCD, в котором одна сторона равна оси, а другая – хорде параболы;

- сторону BC делят на несколько равных частей, а отрезок KC на столько же равных частей;

- из вершины параболы О проводят лучи через точки 1, 2, и т.д., а через точки 1₁, 2₁, и т. д.;

- проводят прямые параллельные оси и определяют точки пересечения лучей с соответствующими параллельными прямыми, например, точку пересечения луча О1 с прямой О1₁, которая принадлежит параболе;

- полученные точки соединяют плавной кривой линией под лекало. Вторая ветвь параболы строится аналогично.

Существуют и другие способы построения параболы.

 

3.4. Построение гиперболы

Гиперболой называется плоская кривая линии, состоящая из двух разомкнутых, симметрично расположенных ветвей в которых разность расстояний от каждой точки до фокусов. F и F₁ величина постоянная и равна расстоянию между вершинами гиперболы A и B.

На рисунке 25 приведен пример построения гиперболы по заданному расстоянию между вершинами A и B – c, хорде гиперболы – b и ее отстоянию от вершины – a. Построение выполняют следующим образом:

- проводят горизонтальную прямую линию на которой откладывают расстояние между вершинами – точки A и B;

- от точки А откдадывают отстояние хорды от вершины гиперболы (точка О), от которой вверх и вниз симметрично откладывают длину хорды (точки C и D);

- строят прямоугольник KNCD. Сторону прямоугольника KC делят на пять равных частей, а OC на такое же число равных частей;

- соединяют вершину A с точками 1, 2, …, C, а вершину B с точками 1¹, 2¹,…, C.

- определяют точки пересечения луча А1 с лучом А1¹, луча А2 с лучом А2¹ и т. д.

- полученные точки пересечения соединяют плавной кривой линией под лекало.

Остальные ветви гиперболы строят как зеркальное отображение построенной ветви.

 

 

Рисунок 24 – Построение Рисунок 25 – Построение ги

параболы перболы

ПОСТРОЕНИЕ ПРОФИЛЕЙ

4.1. Построение швеллера

Построение выполняется в следующем порядке:

- вычерчивают в тонких линиях стенки и наружные линии полок швеллера (рисунок 26а).

- на расстоянии (b-s)/2 откладывают толщину полки t (точки A и B);

- на свободном поле чертежа строят уклон 1:10 (прямые m и n) согласно пункту 2.5;

- через точку A проводят прямую k || m, а через точку B - прямую l || n (рисунок 26б);

- выполняют сопряжение сторон углов в соответствии с пунктом 2.7.1 (рисунок 26в);

- обводят полученный контур профиля сплошной толстой линией;

- проставляют размеры в соответствии с ГОСТ 2.307 - 68;

- выполняют штриховку контура.

Образец выполненного чертежа швеллера приведен на рисунке 26г.

 

 

а) б) в) г)

Рисунок 26 - Этапы построения швеллера

 

4.2. Построение двутавра

Построение двутавра выполняется в следующем порядке:

- вычерчивают в тонких линиях стенки и наружные линии полок двутавра и на расстоянии (b-s)/4 откладывают толщину полки t (точки A, B, C и D) (рисунок 27а);

- на свободном поле чертежа строят уклон 3:25, что соответсвует 12 %, (прямые m и n) согласно пункту 2.5;

- через точки A и C проводят прямые параллельно прямой m, а через точки B и D - прямые параллельно прямой n(рисунок 27б);

- выполняют сопряжение сторон углов в соответствии с пунктом 2.7.1 (рисунок 27в);

- обводят полученный контур профиля сплошной толстой линией;

- проставляют размеры в соответствии с ГОСТ 2.307-68;

- выполняют штриховку контура.

Образец выполненного чертежа двутавра приведен на рисунке 27г.

 

 

а) б) в) г)

Рисунок 27 – Этапы построения двутавра

 

Построение крюка

Построение выполняется в следующем порядке (таблица 7):

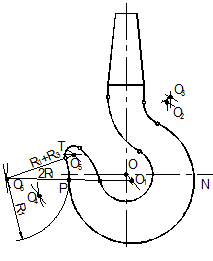
1. Проводим оси и вычерчиваем шейку по размерам, приведенным в таблице 11.

2. Проводим из центра О основную окружность внутри очертания R=D/2.

3. Для построения центра окружности внешнего очертания О₁ из центра О на горизонтальной оси делаем засечку радиусом R= D/2+h (точка N) и проводим прямую п под углом 45⁰ к осям. Из точки N радиусом R₁ на прямой п делаем засечку (точкаО₁).

4. Строим сопряжение внешней окружности с правым прямолинейным контуром верхней части крюка. Сопрягаемая дуга имеет радиус R₂. Центр сопряжения О₂ и точки сопряжения находятся как показано в пункте 2.7.2.

Таблица 7 - Схема построения крюка

1
3

 

 

Продолжение таблицы 7

5	6.1
6.2	6.3

 

 

5. Строим сопряжение внутри окружности диаметром D с левым прямолинейным контуром верхней части крюка радиусом R₁ Центр О₃ находится аналогично п.4.

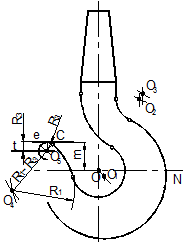
6. Строим очертание носка крюка. Находим центры О₄, О₅, О₆. Носок крюка должен касаться прямой е, проведенной на расстоянии m от горизонтальной оси крюка. Кроме того зев крюка должен быть равен размеру S. Расстояние S измеряется по линии центров О₃, О₄, ограничивающих контур зева.

6.1. Определяем центр О₄ дуги R₁. Для этого делаем две засечки: первую из центра О₃ радиусом R = 2R₁ + S, вторую из центра О радиусом D/2 + R₁. Точка сопряжения Е лежит на линии центров 0 0₄. Из центра О₄ проводим дугу R₁, начиная от точки Е.

6.2. Находим центр О₅ дуги R₃. Для этого сопрягаем прямую, ограничивающую носок сверху, с дугой радиуса R₁ построенную в п. 6.1 На расстоянии R₃ от прямой е проводим прямую t || e. Из О₄ на прямой t делаем засечку дугой R₁- R₃. Точка сопряжения С лежит на линии центров О₄, О₅. Проводим из центра О₅ дугу радиуса R₃.

6.3. Определяем центр О₆ дуги радиуса R₁, сопрягающей носок крюка с внешним контуром крюка. Для этого делаем две засечки: первую из центра О₅ радиусом R₃ + R₁ и вторую из центра О₁ радиусом R₁ + R₁. Точки сопряжений Т и Р лежат на линиях центров О₆ О₅ и О₆ О₁. Из центра О₆ проводим дугу, соединяющую точки Т и Р.

7. Наносим размеры в соответствии с ГОСТ 2.307 – 68, как показано на рисунке 29 (Крюк однорогий).