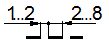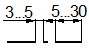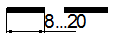Правила оформления чертежей

Министерство образования и науки Украины

Севастопольский национальный технический университет

 

 

 

Геометрическое черчение

с правилами оформления

Чертежей

Методические указания

к самостоятельной работе по дисциплине

«Начертательная геометрия, инженерная

и компьютерная » графика

для студентов по направлению подготовки

0902 – Инженерная механика

0909 – Приборы

0925 – Автоматизация и компьютерно-

интегрированные технологии

1002 – Корабли и океанотехника

дневной и заочной форм обучения

 

Севастополь

 

 

УДК 74 (075)

Геометрическое черчение с правилами оформления чертежей: Методические указания к самостоятельной работе по дисциплине «Начертательная геометрия, инженерная и компьютерная графика» для студентов по направлению подготовки 0902 – инженерная механика, 0909 – приборы, 0925 – автоматизация и компьютерноинтегрированные технологии, 1002 – корабли и океанотехника дневной и заочной форм обучения/ Сост. Медведь А.Ф., Середа В.Г., Смиринская Н.Я. – Севастополь: Изд-во СевНТУ, 2005. - 38 с.

 

Методические указания разработаны с целью:

- ознакомления с описанием графического состава технической документации (основных правил оформления чертежей);

- изложения приемов некоторых геометрических построений при выполнении индивидуальных заданий по теме «Геометрическое черчение».

 

 

Методические указания и задания разработаны на основе рабочей программы «Начертательная геометрия, инженерная и компьютерная графика» в соответствии с учебными планами подготовки специалистов.

 

 

Методические указания рассмотрены и утверждены на заседании кафедры начертательной геометрии и графики (протокол № 4 от 3 декабря 2003 г.)

 

 

Допущено учебно-методическим центром СевНТУ в качестве методических указаний.

 

Рецензент: Харченко А.О., канд. техн. наук, профессор кафедры машиностроения и транспорта, заслуженный изобретатель Украины

 

 

 

СОДЕРЖАНИЕ

Введение…………………………………………………..
1. правила оформления чертежа………………..
1.1. Форматы…………………………………………………
1.2. Масштабы………………………………………………..
1.3. Линии…………………………………………………….
1.4. Шрифты………………………………………………….
1.5. Основная надпись……………………………………….
1.6. Графические обозначения материалов………………...
1.7. Нанесение размеров…………………………………….
2. Геометрические построения…………………..
2.1. Деление отрезка прямой………………………………..
2.1.1. Деление отрезка пополам……………………………
2.1.2. Деление отрезка на равные части……………………
2.1.3. Деление отрезка на пропорциональные части………
2.2. Деление угла на две равные части……………………..
2.3. Деление окружности на равные части…………………
2.4. Построение треугольника………………………………
2.5. Построение уклона.……………………………………..
2.6 Построение конусности...……………………………….
2.7. Сопряжения……………………………………………...
2.7.1. Сопряжение двух прямых линий…………………….
2.7.2. Сопряжение прямой линии с дугой окружности……
2.7.3. Сопряжение двух дуг окружностей..………………...
3. Построение кривых линиИ……………………...
3.1. Построение овала………………………………………..
3.2 Построение эллипса……………………………………...
3.3. Построение параболы…………………………………...
3.4. Построение гиперболы………………………………….
4. Построение профилей……………………………..
4.1. Построение швеллера…………………………………...
4.2. Построение двутавра……………………………………
5. Построение крюка………………………………….
6. указания к выполнению задания…………...
Заключение………………………………………………
БиблиографиЧЕСКИЙ СПИСОК………………………

 

 

Введение

Разработка современного оборудования, машин, механизмов, приборов и других изделий затруднена без знания черчения, необходимого каждому специалисту, связанному с проектированием техники, ее изготовлением, сборкой, монтажом, наладкой и контролем.

Цель работы – освоение основных правил оформления чертежей и овладения техникой геометрических построений.

Изучение машиностроительного черчения начинается с правил оформления чертежей, которые изложены в следующих стандартах: ГОСТ 2.104-68. Основные надписи; ГОСТ 2.301-68. Форматы; ГОСТ 2.302-68. Масштабы; ГОСТ 2.303-68. Линии. ГОСТ 2.304-81. Шрифты чертежные; ГОСТ 2.306-68. Обозначения графические материалов и правила их нанесения на чертежах; ГОСТ 2.307-68. Нанесение размеров и предельных отклонений.

Студенты выполняют задание в объеме два листа формата А3 (420х297) – «Титульный лист» и «Геометрические построения». Варианты задания приведены в таблицах .

Образцы выполненных заданий приведены на рисунках .

 

правила оформления чертежей

Техническая документация любого назначения и содержания имеет единый графический состав: формат, линии, шрифты, основная надпись, графические обозначения материалов.

 

1.1. Форматы

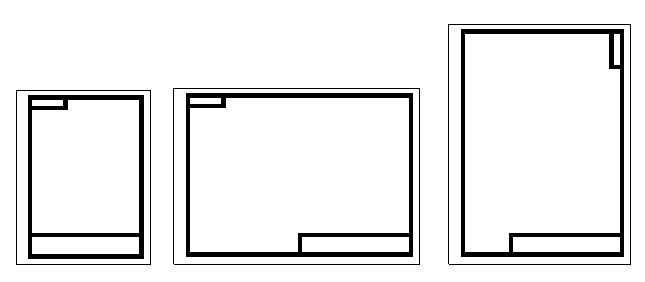
Форматы листов определяются размерами внешней рамки выполненной тонкой линией. Внутренняя рамка чертежа, ограничивающая рабочее поле, выполняется сплошной основной линией на расстояниях от внешней рамки, указанных на рисунке 1.

Обозначение и размеры основных форматов приведены в таблице 1.

 

Таблица 1 - Форматы основные

Обозначение формата	А0	А1	А2	А3	А4
Размеры сторон, мм	Короткой
Длинной

 

Размеры производных форматов образуются путем кратного увеличения короткой стороны основного формата, например, А3х5 производный формат формата А3, размеры которого равны: длина-– L = (5х297) + 1) =1486 мм, а ширина B = 420 мм.

 

 

Рисунок 1 – Вычерчивание внутренней рамки

 

1.2. Масштабы

Масштаб – это отношение линейных размеров изображения на чертеже к истинным размерам предмета.

Наиболее часто применяемые масштабы изображений приведены в таблице 2.

 

Таблица 2 - Масштабы изображений

Масштабы уменьшения	1:2; 1:2,5; 1:4; 1:5; 1:10; 1:20; 1:25; 1:40; 1:50; 1:100;
Натуральная величина	1:1
Масштабы увеличения	2:1; 2,5:1; 4:1; 5:1; 10:1; 20:1; 25:1; 40:1; 50:1; 100:1

 

Масштаб на чертеже проставляется в предназначенной для этого графе и обозначается, например, так 1:1 или 2:1 или 1:5. Если одно из изображений выполнено в масштабе отличном от указанного в основной надписи, то рядом с надписью, относящейся к этому изображению указывают (в скобках без буквы М) его масштаб, например А-А(4:1) или Б(1:2). Иногда на учебных чертежах вычерчивается несколько изделий (деталей) с указанием названия изделия над его изображением. Если одно из изделий выполнено в масштабе, не совпадающим с масштабом указанным в основной надписи, то рядом с названием изделия в скобках указывается масштаб, например, Крюк (2:1).

 

1.3. Линии

При выполнении чертежей используются линии наименование, начертание и толщина которых должна соответствовать ГОСТ 2.303-68 (таблица 3).

В учебных чертежах основным линиям (линиям видимого контура) следует придавать толщину S = (0,8…1.0) мм, линиям штриховым (линиям невидимого контура) – 0,4…0.5 мм, разомкнутым линиям – 1,5S, а остальным линиям – 0,25…0,3 мм. Студентам следует научиться различать толщину линий с точностью до 0,1…0,15 мм. Как правило, учебные чертежи сначала выполняют тонкими, но ясно различимыми линиями. Нужную толщину линиям придают при обводке.

 

Таблица 3 - Линии чертежа по ГОСТ 2.303-68

Начертание	Вид	Толщина, мм	Назначение
	Сплошная толстая основная	S=0,5…1,4	Линии видимого контура
	Сплошная тонкая	S1=(1/3…1/2) S	Линии выносные и размерные, линии штриховки, услов-ные линии перехода
	Сплошная волнистая	Линии обрыва
	Штриховая	Линии невидимого контура
	Штрихпунк-тирная	Линии осевые и центровые
	Штрихпунк-тирная с дву-мя точками	Линии крайнего положения деталей, линии сгиба
	Разомкнутая	S2=1,5S	Линии положения плоскости разреза, сечения

 

 

Штрихи и интервалы между штрихами должны быть соответственно равны между собой.

Штрихпунктирные и центровые линии следует заменять сплошными тонкими, если диаметр окружности в изображении имеет размер менее 12 мм. Линии со штрихами должны пересекаться и заканчиваться штрихами.

Пример применения линий на чертеже приведен на рисунке 2.

 

 

 

Рисунок 2 – Пример вычерчивания линий

 

 

1.4. Шрифты

Чертежный шрифт – это буквы, цифры и знаки на чертеже.

Размер шрифта – это высота прописных букв. Буквы и цифры имеют угол наклона 75^о или 90^о. Толщина d линии шрифта зависит от

типа и высоты шрифта: Пример начертания букв типа А и Б приведен на рисунке 3.

- тип А с наклоном 75⁰ с d = (1/14)h (рисунок 3а);

- тип А без наклона с d = (1/14)h (рисунок 3б);

- тип Б с наклоном 75⁰ с d = (1/10)h(рисунок 3в);

- тип Б без наклона с d = (1/10)h (рисунок 3г).

 

 

 

 

а) б) в) г)

Рисунок 3 – Типы шрифтов

 

Пример написания букв и цифр типа Б с наклоном 75⁰ приведен на рисунке 4.

Рисунок 4 – Написание букв и цифр

Размеры букв и цифр рекомендуемого шрифта типа Б приведены в таблице 4.

Таблица 4 – Размеры шрифта типа Б, мм

Размер шрифта	2,5	3,5	5,0	7,0	10,0	14,0	20,0
Высота прописных букв,h	2,5	3,5	5,0	7,0	10,0	14,0	20,0
Высота строчных букв	1,8	2,5	3,5	5,0	7,0	10,0	14,0
Расстояние меж- ду буквами, a	0,5	0,7	1,0	1,4	2,0	2,8	4,0
Минимальный шаг строк, b	4,3	6,0	8,5	12,0	17,0	24,0	34,0
Минимальное расстояние между словами, e	1,5	2,1	3,0	4,2	6,0	8,4	12,0
Толщина линий шрифта, d	0,25	0,35	0,5	0,7	1,0	1,4	2,0
Ширина прописных букв и цифр	Ж, Ш, Щ, Ф, Ъ	2,0	2,8	4,0	5,6	8,0	11,2	16,0
А, Д, М, Х, Ы, Ю	1,8	2.5	3,5	4,9	7,0	9,8	14,0
Г, З, Е, С, 1, 2, 3, 4, 5, 6, 7, 8, 9, 0	1,3	1,8	2,5	3,5	5,0	7,0	10,0
Остальные буквы	1,5	2,1	3,0	4,2	6,00	8,4	12,0
Ширина строчных букв	С	1,0	1,4	2,0	2,8	4,0	5,6	8,0
Т, Ж, Ш, Щ, Ф	1,8	2,5	3,5	5,0	7,0	10,0	14,0
М, Ы, Ю	1,5	2,1	3,0	4,2	6,00	8,4	12,0
Остальные буквы	1,3	1,8	2,5	3,5	5,0	7,0	10,0

 

Прописные буквы латинского алфавита A, B, C, E, K, M, O, P, T выполняются как прописные буквы русского алфавита А, В, С, Е, К, М, О, Р, Т, соответственно.

Строчные буквы латинского алфавита a, c, e, o, p выполняются как строчные буквы русского алфавита а, с, е, о, р соответственно.

 

1.5. Основная надпись

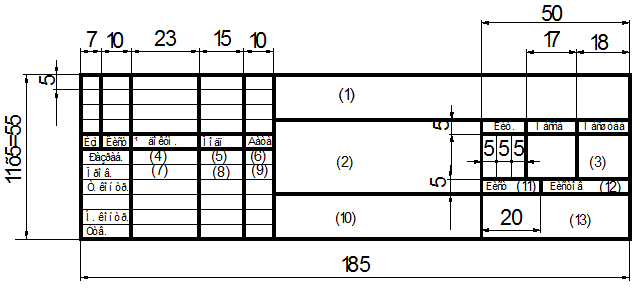
Основная надпись является частью чертежа в которой содержится значительная информация об изделии изображенном на самом чертеже. Основная надпись состоит из граф вычерчиваемых сплошными толстыми и тонкими линиями по ГОСТ 2.303-68 по размерам, указанным на рисунке 5. На учебных чертежах заполняются только графы, обозначенные числами в скобках.

В графе 1 (рисунок 5)и дополнительной рамке (рисунок 6) наносится обозначение чертежа, состоящее из группы букв и цифр, отделенных друг от друга точками, например, СНТУ.101500.001, где СНТУ сокращенное наименование ВУЗ'а; 1 – номер расчетно-графического задания; 015 – номер варианта; 001 – номер задания.

В графе 2 указывается наименование изделия в соответствии с ГОСТ 2.109-73. Наименование записывается в именительном падеже единственного числа. Если наименование состоит из нескольких слов, то на первое место помещают имя существительное, например: «Гайка накидная».

В графе 3 указывается масштаб, в котором выполнено изображение изделия. В графах 4 и 5 - фамилия и подпись студента соответственно, а в графе 6 – дата подписания чертежа студентом. В графах 7 и 8 – фамилия и подпись преподавателя принявшего чертеж, а в графе 9 – дата подписания чертежа преподавателем.

Графа 10 заполняется только на чертежах деталей. В ней указывается обозначение материала, из которого будет изготовлена деталь, например, Ст.3 ГОСТ 380-94, где Ст.3 – марка материала и номер ГОСТ’а в котором указаны требования к качествам материала.

Порядковый номер листа (графа 11) проставляется, если чертеж (задание) выполнено на двух и более листах. На документах

 

 

Рисунок 5 – Основная надпись

 

состоящих из одного листа, графу 11 не заполняют. В графе 12 количество листов проставляется только на первом листе.

В графе 13 указывается наименование кафедры и номер группы, например: «Кафедра НГ и Г, группа ЭД 12д».

Основная надпись располагается в правом нижнем углу чертежа. Для формата А4 она располагается только вдоль короткой стороны листа (рисунок 6а), а для остальных форматов – как вдоль длинной (рисунок 6б), так и вдоль короткой стороны листа (рисунок 6в).

На чертежах кроме основной надписи вычерчивается дополнительная рамка повернутая на:

- 180⁰ для формата .А4 (рисунок 6а) и для форматов больше А4 при расположении основной надписи вдоль длинной стороны (рисунок 6б);

- 90⁰ для форматов больше А4 при расположении основной надписи вдоль короткой стороны (рисунок 6в).

а) б) в)

Рисунок 6 – Расположение основной надписи и дополнительной рамки на чертежах

 

Все надписи в графах выполняются чертежным шрифтом типа Б высотой: 10 мм - графа 1; 7 мм - графа 14, 5 мм - графы 2, 3 и 13.

Остальные графы выполняются размером 2,5 мм. Надпись в дополнительной рамке выполняется повернутой на:

- 180⁰ для формата .А4 (рисунок 6а) и для форматов больше А4 при расположении основной надписи вдоль длинной стороны (рисунок 66);

- 90⁰ для форматов больше А4 при расположении основной надписи вдоль короткой стороны (рисунок 6в).

 

1.6. Графические изображения материалов

При выполнении разрезов и сечений графические обозначения материалов должны соответствовать ГОСТ 2.306-68 «Обозначения графические материалов и правила их нанесения на чертежах». В таблице 5 приведены графические изображения материалов, наиболее часто встречающиеся при выполнении заданий по машиностроительному черчению.

 

Таблица 5 – Графические изображения материалов

Материал	Обозначение
Металлы и твердые сплавы
Неметаллические материалы
Стекло и другие прозрачные материалы

Линии штриховки проводятся сплошной тонкой линией с шагом до 10 мм в зависимости от площади штриховки. Рекомендуемый шаг штриховки – 1…3 мм. Частота и угол наклона штриховки должны быть одинаковыми для всех сечений одной и той же детали, выполненных в одном масштабе.

 

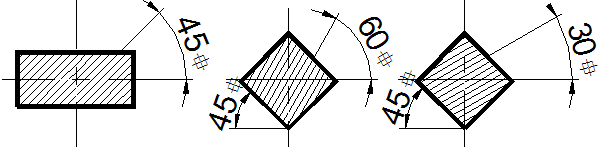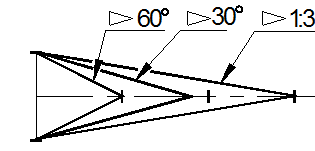
Угол наклона линий штриховки - 45^о к линии рамки чертежа (рисунок 7). Если линии штриховки, проведенные под углом 45^о к линии рамки чертежа, совпадают по направлению с контурными линиями изображения, то угол наклона линий штриховки необходимо принимать равным 60^о или 30^о (рисунок 7).

Рисунок 7 – Примеры выполнения штриховки

Штриховка смежных деталей отличается по частоте и направлению линий (рисунок 8).

Узкие площади сечений, ширина которых на чертеже не превышает 2 мм, допускается показывать зачерненными с оставлением просветов между смежными сечениями не менее 0,8 мм (рисунок 9).

 

Рисунок 8 – Штриховка Рисунок 9 – Штриховка смежных смежных деталей деталей с узкими площадями сечений

 

1.7. Нанесение размеров

Правила нанесения размеров на чертежах определяются ГОСТ 2.307-68.

Размер – это числовое значение линейной или угловой величины изделия или его элементов в выбранных единицах.

Линейные размеры на чертежах указывают в миллиметрах без обозначения единиц измерения.

В целях упорядочения размеров приняты округленные значения чисел по ГОСТ 6636-69 «Нормальные линейные размеры».

Угловые размеры указывают в градусах, минутах, секундах, например 30^/, 2⁰, 2⁰30^/, 2⁰30^/15^//, или в виде соотношения двух катетов прямого угла, например, 1:8.

Общее количество размеров на чертеже должно быть минимальным, но достаточным для изготовления и контроля изделия.

Размер наносится на чертеже только один раз и на том изображении, где лучше читается форма этой части детали. Не допускается повторять размеры одного элемента на разных изображениях.

Размеры на чертежах указывают размерными числами, выносными и размерными линиями. При нанесении размера прямолинейного отрезка размерную линию проводят параллельно этому отрезку, а выносные линии перпендикулярно размерной линии.

При нанесении размера угла размерную линию проводят в виде дуги с центром в его вершине, а выносные линии – радиально. При нанесении размера дуги окружности размерную линию проводят концентрично самой дуге, а выносные линии – параллельно биссектрисе угла.

Размерную линию ограничивают стрелками, которые острыми концами упираются в соответствующие выносные линии. Допускается проводить размерные линии к линиям видимого контура, осевым, центровым и другим линиям. Выносные линии должны выходить за концы выносных линий на 1…5 мм.

Расстояние размерной линии от параллельной ей линии контура должно быть не менее 10 мм, а между размерными линиями не менее 7 мм.

Допускается проводить размерные линии с обрывом при указании размера диаметра окружности, при этом обрыв размерной линии делают дальше осевой линии, и при нанесении размеров от базы, если она не изображена на чертеже. При изображении изделия с разрывом размерная линия не прерывается.

Знаки, сопровождающие размерные числа приведены в таблице 6.

Таблица 6 - Пример использования условных знаков

Диа-метр	Радиус	Квад-рат	Тол-щина	Длина	Дуга	Конус-ность	Уклон
Ø12	R45	□15	S10	L100		< 1:5	1:5

 

Перед размерным числом диаметра сферы ставится знак ¡, например ¡ Ø 20 – сфера диаметром 20 мм.

При применении линий обрывов на чертеже размерные линии следует проводить полностью, при этом. размерные числа должны соответствовать действительным размерам.

При нанесении размеров не допускается:

- проставлять размеры от линий невидимого контура;

- использовать в качестве размерных линий контурные, осевые, центровые и выносные линии;

- разделять или перечеркивать размерные числа какими бы то ни было линиями;

- наносить размерные числа в месте пересечения двух линий.

 

 

2 . Геометрические построения

Контуры изображаемых деталей образуют линии – прямые, коробовые и лекальные кривые. При вычерчивании изображений применяют следующие построения:

- деление отрезков и углов;

- деление окружности на равные части;

- сопряжения линий;

- построение уклона и конусности.

 

2.1. Деление отрезка прямой

2.1.1. Деление отрезка пополам

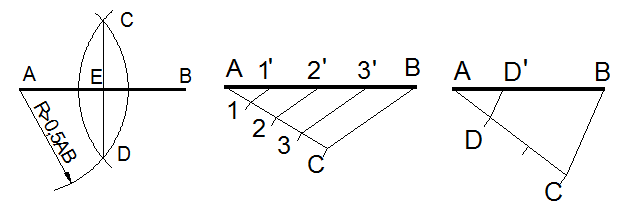
Деление отрезка пополам выполняют следующим образом (рисунок 10а):

- из точек A и B радиусом R > 0,5AB проводят дуги до пересечения в точках C и D;

- через точки C и D проводят прямую линию, которая делит отрезок пополам (точка E).

 

 

а) б) в)

Рисунок 10 – Деление отрезка

 

2.1.2. Деление отрезка на равные части

Деление отрезка на равные части выполняют следующим образом (рисунок 10б):

- из точки A отрезка AB под произвольным углом проводят прямую линию и делят ее на заданное число равных отрезков (точки 1, 2, 3, C);

- точку C соединяют с точкой B;

- из точек 1, 2, и 3 проводят прямые параллельно отрезку BC, до пересечения с отрезком AB в точках 1', 2' и 3'.

 

2.1.3. Деление отрезка на пропорциональные части

Деление отрезка на пропорциональные части выполняют в следующей последовательности (рисунок 10в):

- из точки A отрезка AB под произвольным углом проводят прямую линию и делят ее на равные части, например, три;

- точку C соединяют с точкой B;

- из точки D проводят прямую параллельно отрезку BC.

 

2.2. Деление угла на две равные части

Деление угла на равные части выполняют в следующей последовательности (рисунок 11):

- из вершины угла B произвольным радиусом R проводят дугу до пересечения со сторонами угла в точках D и C;

- из точек D и C радиусом R₁ проводят дуги до пересечения в точке K;

- соединяют точки B и K (отрезок BK делит угол пополам).

 

 

Рисунок 11 – Деление угла Рисунок 12 – Деление окружности

2.3. Деление окружности на равные части

Пример деления окружности на равные части проведен на рисунке 12.

Справа от оси CD показано деление окружности на три, шесть и двенадцать частей, для чего:

- из точки A радиусом R окружности проводят дугу до пересечения с окружностью в точках F и E. Отрезок FE отсекает треть окружности, AF – шестую, а DF – двенадцатую часть окружности.

Слева над осью АВ показано деление окружности на пять и десять частей (выше оси AB), для чего:

- из точки A радиусом R окружности проводят дугу до пересечения с окружностью в точках F и E;

- из точки E строят перпендикуляр до пересечения с осью AB (точка) O₁;

- из точки O₁ радиусом R₁=O₁C проводят дугу до пересечения с

 

осью AB (точка М). Отрезок CM делит окружность на пять, а отрезок OM на десять равных частей.

Слева ниже оси AB показано деление окружности на четыре и восемь равных частей, для чего:

- соединяют точки B и D;

- делят отрезок BD пополам (см. пункт 2.1.1);

- из центра O проводят серединный перпендикуляр до пересечения с окружностью (точка K). Отрезок BD делит окружность на четыре, а отрезок KD – на восемь равных частей.

 

2.4. Построение треугольника

Пример построения треугольника по трем заданным сторонам приведен на рисунке 13.

 

 

Рисунок 13 – Построение треугольника

 

Из концов стороны АС треугольника радиусами R=n и R₁=m проводят дуги до пересечения в точке В. Полученную точку соединяют с точками А и С.

 

2.5. Построение уклона

Уклоном iпрямой АС относительно прямой АВ называется тангенс угла между этими прямыми, т.е. i = (h/l) = tga, где h – разность аппликат концов отрезка АС; l– разность абсцисс отрезка АВ (рисунок 14).

Уклон на чертеже в соответствии с ГОСТ 2.307 - 68 указывают с помощью линии-выноски, на полке которой наносят знак и значение уклона.

Уклон обозначается знаком « Ð », а величина его выражается дробью, в процентах и градусах, например, Ð 1:5, Ð 20 %, Ð 15⁰. Расположение знака уклона должно соответствовать определяемой линии: одна из прямых знака должна быть параллельна катету (АВ), а другая - наклонена под углом 30⁰ к ней, при этом острие знака всегда направлено в сторону уклона.

На рисунке 15 показано построение и обозначение различных уклонов.

 

 

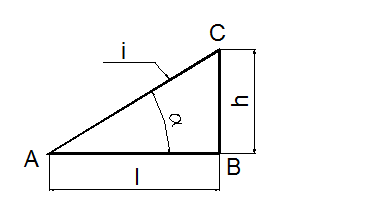
Рисунок 14 – Опре- Рисунок 15 – Обозначение уклона

деление величины уклона

2.6. Построение конусности

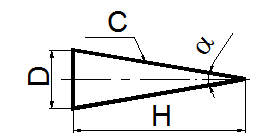
Конусностью C называется отношение диаметра окружности основания прямого конуса к его высоте C = D/2H = tga/2 (рисунок 16).

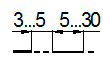
Конусность на чертеже в соответствии с ГОСТ 2.307 - 68 указывают с помощью линии-выноски, на полке которой наносят знак и значение конусности.

Конусность обозначается знаком «>», острие которого направлено в сторону вершины конуса, а величина её выражается дробью или в градусах, например, > 1:5, >30⁰. На рисунке 17 показано построение и обозначение конусности.

 

 

Рисунок 16 – Опреде- Рисунок 17 – Обозначение

ление конусности конусности

 

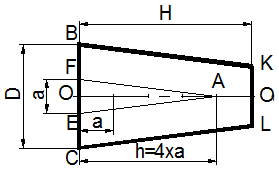
Построение усеченного конуса с заданным диаметром большего основания D, высотой H и конусностью равной 1:4 (рисунок 18) выполняется в следующей последовательности:

- откладываем высоту конуса H=ОО₁ на оси симметрии;

- через точку O проводим перпендикуляр, на котором симметрично от оси откладываем диаметр большого основания D=BC;

- из точки O по оси OO₁ откладываем четыре равных отрезка произвольной длины OA=4a;

- от точки O симметрично от оси откладываем отрезок a=FE;

- соединив точки F и E с точкой A, получим вспомогательный конус с конусностью 1:4;

- через точки B и C проводим прямые линии параллельно образующим вспомогательного конуса до пересечения с перпендикуляром, проведенным через точку O₁. Полученные точки K и L ограничивают величину малого основания усеченного конуса.

2.7. Сопряжения

Очертание многих деталей, узлов состоит из линий, плавно переходящих одна в другую, называемых сопряжением. Из многообразия возможных сопряжений можно выделить следующие:

- сопряжение двух прямых линий дугой окружности;

- сопряжение прямой линии с дугой окружности при помощи другой дуги окружности;

- сопряжение двух дуг окружности при помощи третьей дуги.

 

Рисунок 18 – Построение Рисунок 19 – Сопряжение конусности сторон угла

 

2.7.1. Сопряжение двух прямых линий

Сопряжение двух сторон угла дугой окружности (рисунок 19) выполняется следующим образом:

- параллельно сторонам угла AB и BC на расстоянии равном радиусу дуги R проводят прямые линии l и m до пересечения в точке О;

- из точки O опускают перпендикуляры на сопрягаемые стороны. Точки D и E являются точками сопряжения;

- из точки O радиусом R = OD = OE проводят дугу плавно переходящую в прямые линии.

 

2.7.2. Сопряжение прямой линии с дугой окружности

Рассмотрим два случая сопряжения: внешнее и внутреннее.

Внешнее сопряжение прямой линии с дугой окружности выполняется следующим образом:

- из центра О строится дуга радиусом R₂=R+R₁, где R₁ – радиус сопряжения;

- на расстоянии R₁ от заданной прямой n проводится параллельная прямая m;

- определяется центр О₁ сопряжения как результат пересечения дуги окружности радиусом R₂ с прямой m;

- из центра О₁ строится дуга AB сопряжения радиусом R₁.

Внутреннее сопряжение прямой с дугой окружности выполняется так:

- из заданного центра заданной дуги окружности строится дуга радиусом R₂=R-R₁, где R₁ – радиус сопряжения;

- на расстоянии R₁ от заданной прямой n проводится параллельная прямая m;

- из полученного центра О₁ строится дуга AB сопряжения радиусом R₁.

а) б)

Рисунок 20 – Сопряжение дуги окружности с прямой линией

 

2.7.3. Сопряжение двух дуг окружности

Различают внешнее, внутреннее и смешанное сопряжение двух дуг третьей дугой. Во всех трех случаях необходимо определить положение центра дуги сопряжения О₂ и точек сопряжения A и B.

Внешнее сопряжение (рисунок 21а) выполняется следующим образом:

- из центров дуг окружностей О и О₁ радиусами R₃=R+R₂ и R₄=R₁+R₂ соответственно, проводим дуги до их пересечения в точке О₂;

- соединяем центр сопряжения О₂ с центрами дуг окружностей прямыми линиями О₂О и О₂ О₁;

- из центра сопряжения О₂ радиусом R₂ проводим дугу между точками сопряжения A и B.

 

 

 

а) б) в)

Рисунок 21 –Сопряжение двух дуг окружностей

 

Пример выполнения внутреннего сопряжения приведен на рисуноке 21б):

- из центров дуг окружностей О и О₁ радиусами R₃= R₂-R и R₄=R₂- R₁ проводим дуги до их пересечения в точке О₂;

- соединяем центр сопряжения О₂ с центрами дуг окружностей прямыми линиями О₂О и О₂ О₁;

- из центра сопряжения О₂ радиусом R₂ проводим дугу между точками сопряжения A и B.

Смешанное сопряжение (рисунок 21в) выполняется следующим образом:

- из центров дуг окружностей О и О₁ радиусами R₃=R+R₂ и R₄=R-R₂ соответственно, проводим дуги до их пересечения в точке О₂;

- соединяем центр сопряжения О₂ с центрами дуг окружностей прямыми линиями О₂О и О₂ О₁;

- из центра сопряжения О₂ радиусом R₂ проводим дугу между точками сопряжения A и B.