 |
Главная |
Метод Тейлора второго порядка
|
из
5.00
|
При  из формулы (6) получаем
из формулы (6) получаем
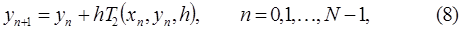
где

Метод Рунге-Кутта.
Метод Рунге-Кутта имеет тот же порядок точности, что и метод Тейлора, но исключает необходимость вычисления значений частных производных от правой части дифференциального уравнения 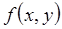 . Основная идея метода состоит в замене функции
. Основная идея метода состоит в замене функции  в формуле (6) другой функцией
в формуле (6) другой функцией  , не требующей вычисления частных производных от
, не требующей вычисления частных производных от 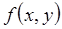 и удовлетворяющей условию
и удовлетворяющей условию

где  - константа, не зависящая от
- константа, не зависящая от 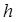 . Таким образом, алгоритм метода Рунге-Кутта имеет вид:
. Таким образом, алгоритм метода Рунге-Кутта имеет вид:

где  удовлетворяет условию (9). Очевидно, метод (10) имеет ту же алгоритмическую ошибку, что и метод Тейлора. Алгоритм (10) принято называть методом Рунге-Кутта порядка
удовлетворяет условию (9). Очевидно, метод (10) имеет ту же алгоритмическую ошибку, что и метод Тейлора. Алгоритм (10) принято называть методом Рунге-Кутта порядка 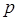 .
.
Функцию  разыскивают в виде:
разыскивают в виде: 

где


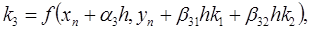


В формулах (11) коэффициенты  и
и  находятся из условия (9).
находятся из условия (9).
Метод Рунге-Кутта первого порядка.
При 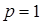 получаем из (11)
получаем из (11)

Сравнивая  с
с  , немедленно получаем из условия (9), что
, немедленно получаем из условия (9), что  . Таким образом метод Рунге-Кутта первого порядка совпадает с явным методом Эйлера:
. Таким образом метод Рунге-Кутта первого порядка совпадает с явным методом Эйлера:

Метод Рунге-Кутта второго порядка.
При  получаем из (11)
получаем из (11)

Разлагая 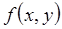 во втором слагаемом в (12) по формуле Тейлора в точке
во втором слагаемом в (12) по формуле Тейлора в точке  получаем
получаем
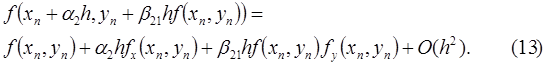
Подставляя (13) в (12), имеем

 Сравнивая
Сравнивая  и (14), получаем из условия (9) нелинейную систему уравнений для определения коэффициентов
и (14), получаем из условия (9) нелинейную систему уравнений для определения коэффициентов  :
:
Отсюда следует, что для различных  существует целое семейство методов Рунге-Кутта второго порядка с коэффициентами
существует целое семейство методов Рунге-Кутта второго порядка с коэффициентами  и
и
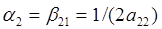 :
:


Приведем примеры алгоритмов метода Рунге-Кутта второго порядка.
Метод Хьюна (модифицированный метод трапеций).
В этом случае 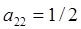 ,
, 
 Из (15) получаем алгоритм метода Хьюна
Из (15) получаем алгоритм метода Хьюна

Модифицированный метод Эйлера.
В этом случае  ,
, 
 Из (15) получаем алгоритм модифицированного метода Эйлера
Из (15) получаем алгоритм модифицированного метода Эйлера

Метод Рунге-Кутта четвертого порядка.
Наиболее часто в вычислительной практике используется метод Рунге-Кутта четвертого порядка, алгоритм которого определяется формулами

где





Отметим, что если правая часть дифференциального уравнения 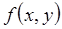 не зависит от
не зависит от 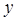 , то формула (18) совпадает с квадратурной формулой Симпсона. (Решение задачи Коши
, то формула (18) совпадает с квадратурной формулой Симпсона. (Решение задачи Коши  равносильно вычислению интеграла
равносильно вычислению интеграла  ).
).
Замечание.Метод (18) часто называют просто «методом Рунге-Кутта» без всяких указаний на порядок. Локальная алгоритмическая ошибка этого метода не превосходит 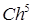 , где
, где  - константа, не зависящая от
- константа, не зависящая от  . Однако оценить
. Однако оценить 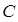 не просто. Это существенный недостаток метода Рунге-Кутта. Грубое оценочное правило выбора шага
не просто. Это существенный недостаток метода Рунге-Кутта. Грубое оценочное правило выбора шага  предложено Коллатцом: если для некоторой точки
предложено Коллатцом: если для некоторой точки  величина
величина 
 больше нескольких сотых, то шаг
больше нескольких сотых, то шаг 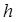 уменьшают.
уменьшают.
|
из
5.00
|
Обсуждение в статье: Метод Тейлора второго порядка |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

