Устойчивость методов полиномиальной аппроксимации

При анализе устойчивости метода полиномиальной аппроксимации обычно обращаются к тестовой задаче Коши

где 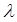- комплексный параметр.

Применим алгоритм (22) к решению задач (38), получим

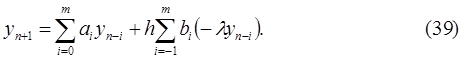
Преобразуем (39) в эквивалентное разностное уравнение

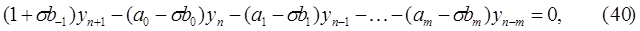
где .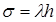

Положив в (40) 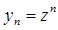, получим после сокращения на 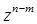многочлен степени :

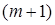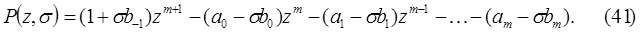
Многочлен (41) будем называть характеристическим многочленом метода полиномиальной аппроксимации (22).

Общее решение разностного уравнения (40) определяется выражением

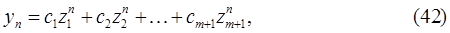
где 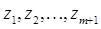- 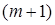различных корней характеристического многочлена (41), 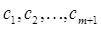- произвольные постоянные, значения которых находятся из стартовых значений 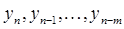решения. Если характеристический многочлен (41) имеет кратный корень 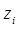( 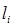- его кратность), то соответствующее слагаемое в формуле (42) общего решения будет иметь вид

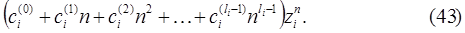
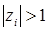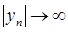Заметим, что если , то при 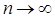(даже в том случае, когда корень 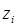- простой). Если 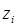- корень кратност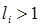и и 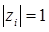, то из (43) следует, что 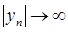при .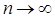

Замечание.При 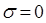значение 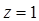является простым корнем характеристического многочлена 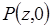тогда и только тогда, когда .

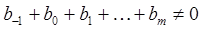Теорема(критерий устойчивости методов полиномиальной аппроксимации).

Состоятельный метод полиномиальной аппроксимации (22), удовлетворяющий условию 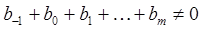, устойчив (в том смысле, что локальная алгоритмическая ошибка метода и ошибка округления остаются ограниченными при достаточно малой величине шага 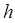) тогда и только тогда, когда все корни 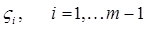многочлена

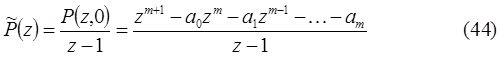
таковы, что 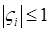, а те корни, для которых 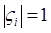, простые.

Корни многочлена (44) принято называть паразитными.

Замечание.Методы Адамса-Башфорта и Адамса-Мултона устойчивые. Действительно, для этих методов 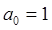, 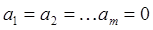. Поэтому

.

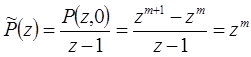Здесь все корни многочлена 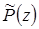равны нулю и, следовательно, лежат внутри единичного круга.

Обозначим через 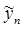- решение уравнения

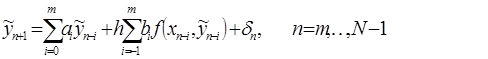
со стартовыми значениями ( ).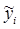

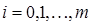Теорема (оценка глобальной погрешности многошагового метода полиномиальной аппроксимации).

Пусть выполнены следующие условия:

1. Правая часть дифференциального уравнения 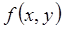определена непрерывна в области 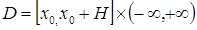и существует константа 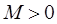, не зависящая от 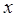такая, что в области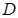

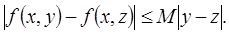
2. Пусть 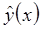- точное решение уравнения задачи Коши (1) имеет на отрезке 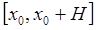непрерывные производные до порядка , .

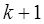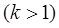3. Метод полиномиальной аппроксимации (22) является состоятельным и .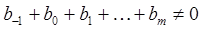

4. При достаточно малом 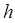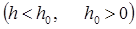все корни 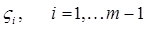многочлена

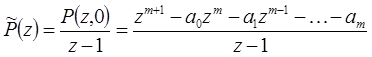
таковы, что 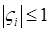, а те корни, для которых 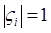, простые.

 

Тогда для глобальной ошибки метода (22) справедлива оценка

 

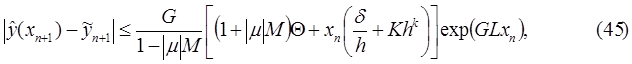
где 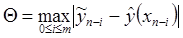, , 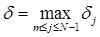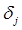-локальная ошибка округления на 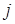-ом шаге, 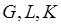- постоянные, зависящие от коэффициентов формулы (22) и правой части дифференциального уравнения 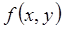и независящие от , .

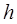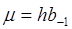Из (45) следует, что глобальная ошибка метода полиномиальной аппроксимации состоит из трех частей:

1) ошибка при вычислении стартовых значений,

2) суммарная алгоритмическая ошибка метода, характеризуемая величиной 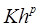, убывающая с уменьшением ,

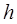3) ошибка округления, представленная членом 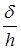, который растет с уменьшением .

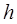Погрешность, очевидно, растет с увеличением длины отрезка, на котором разыскивается решение.

Замечание.Все описанные методы решения задачи Коши (1) переносятся на системы дифференциальных уравнений

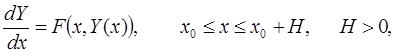
где

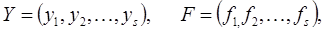
или

…….

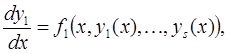
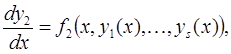
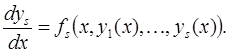
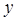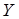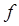Формулы сохраняются в прежнем виде, нужно только заменить на , на 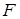. В оценках погрешности абсолютная величина заменяется на норму вектора.

6. Задание.Найдите на отрезке 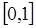решение задачи Коши для системы обыкновенных дифференциальных уравнений

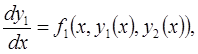
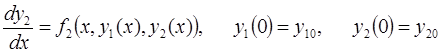
с точностью 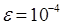, методами Рунге-Кутта, Адамса-Башфорта четвертого порядка и прогноза-коррекции (используя для прогноза алгоритм (37) и коррекции – метод Адамса-Мултона четвертого порядка).

Варианты заданий.

№ варианта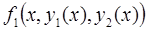
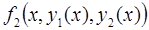
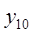
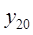
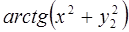
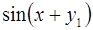
			0,5	1,5
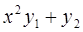
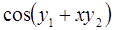
			-1
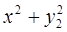
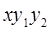
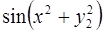
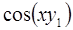
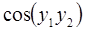
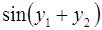
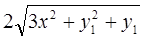
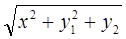
			0,5	1,2
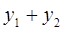
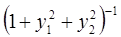
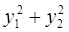
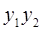
			-1
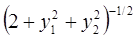
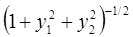
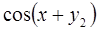
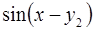
			0,7	-0,5
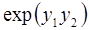
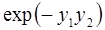
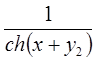
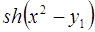
			0,2
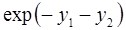
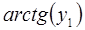
				-1
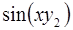
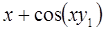
№ варианта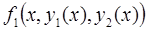
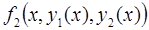
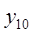
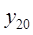
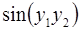
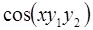
			-1
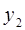
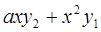
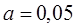
					1/6
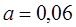
			1/7
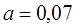
			0,125
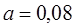
			1/9
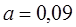
			0,1
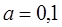
			1/11
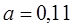
			1/11
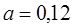
			1/12
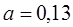
			1/13
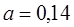
			1/14
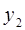
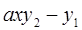
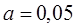
					1/6
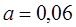
			1/7
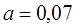
			0,125
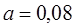
			1/9
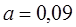
			0,1
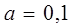
			1/11
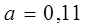
			1/12

Приложение.Для выполнения задания можно использовать следующие процедуры (на языке Паскаль):

 

1) Процедура rung, реализующая алгоритм метода Рунге-Кутта четвертого порядка (18):

 

Procedure rung(h:real; var x0:real;var y0:vector; n:integer);

{Входные параметры:

h – шаг интегрирования системы;

x0 – стартовое значение аргумента;

y0 – массив, содержащий значения решения системы в точке x0;

n - размерность системы.

Выходные параметры:

y0 – массив, содержащий значения решения системы в точке x0+h.

Здесь vector - одномерный массив порядка n}

var

i:integer;

begin

f(x0,y0,k1); for i:=1 to n do yt[i]:=y0[i]+0.5*h*k1[i];

f(x0+0.5*h,yt,k2); for i:=1 to n do yt[i]:=y0[i]+0.5*h*k2[i];

f(x0+0.5*h,yt,k3); for i:=1 to n do yt[i]:=y0[i]+h*k3[i];

f(x0+h,yt,k4); x0:=x0+h;

for i:=1 to n do y0[i]:=y0[i]+(h/6)*(k1[i]+2*k2[i]+2*k3[i]+k4[i])

end;

 

2) Процедура ad , реализующая алгоритм метода Адамса-Башфорта четвертого порядка (см. Таблицу 1):

 

Procedure ad(h:real;var yt:start;var y0:vector);

{Входные параметры:

h – шаг интегрирования системы;

yt – двумерный массив порядка (n,4)(n-размерность системы),столбцы

которого являются решениями системы в четырех стартовых точках.

Выходные параметры:

y0 – массив, содержащий решение системы в точке, отстоящей на 4h от

первой стартовой.

Здесь start – двумерный массив порядка (n,4), vector - одномерный

массив порядка n, kof – одномерный массив порядка 4.}

var

i,j:integer; kf:kof;

begin

kf[1]:=-9.0/z; kf[2]:=37.0/z; kf[3]:=-59.0/z; kf[4]:=55.0/z;

for i:=1 to n do

for j:=1 to 4 do

y0[i]:=y0[i]+h*yt[j,i]*kf[j]

end;

3) Процедура ad_mult, реализующая алгоритм метода прогноза-коррекции: прогноз - явный метод (37), коррекция - метод Адамса-Мултона четвертого порядка (см. Таблицу 2).

 

Procedure ad_mult(x0,h,eps:real;ys:start;var yc:vector);

{ {Входные параметры:

x0 – первая стартовая точка решения системы;

h - шаг интегрирования системы;

eps- значение 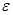в условии окончания итерационного процесса при

коррекции решения ;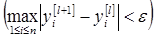

ys – двумерный массив порядка (n,3) (n-размерность системы),

столбцами которого являются решения системы в трех стартовых

точках.

Выходные параметры:

yc - массив, содержащий решение системы в точке, отстоящей на 3h от

первой стартовой.

Здесь start – двумерный массив порядка (n,3), vector - одномерный

массив порядка n, kof – одномерный массив порядка 4.}

var

i,j :word;

yt :start; {

yp,y :vector; {

ka_m :kof;

x :real;

begin

yp:=ys[3];

for j:=1 to 3 do f(x0+j*h,ys[j+1],yt[j]);

ka_m[1]:=1/z; ka_m[2]:=-5/z; ka_m[3]:=19/z; ka_m[4]:=9/z;

for i:=1 to n do yp[i]:=yp[i]+2*h*yt[3,i]; {прогноз}

f(x0+4*h,yp,yt[4]);

yc:=ys[4];

for i:=1 to n do

for j:=1 to 4 do

yc[i]:=yc[i]+h*yt[j,i]*ka_m[j];

while nr(yp,yc)>=eps do

{nr – имя функции,вычисляющей норму разности двух векторов}

begin yp:=yc; y:=ys[4];

f(x0+4*h,yc,yt[4]);

for i:=1 to n do

for j:=1 to 4 do

y[i]:=y[i]+h*yt[j,i]*ka_m[j];

yc:=y

end

end;

function nr(z,z1:vector):real;

{vector - одномерный массив порядка n}

var i :word;

q :real;

begin

q:=0; for i:=1 to n do

if abs(z1[i]-z[i])>=q then q:=abs(z1[i]-z[i]);

nr:=q

end;

 

Составитель – Трофимов Валерий Павлович

Редактор - Бунина Т.Д.