Расчетные нагрузки и их комбинации. Общие положения расчетных нагрузок и их комбинаций для стреловых и мачтовых кранов

Общие положения расчетных нагрузок и их комбинаций для стреловых и мачтовых кранов общего назначения приведены в табл. 3 и 4. Вес металлических конструкций без оголовков решетчатых стрел и мачт квадратного или треугольного сечения с размерами боковой стороны 500 – 1000 мм составляет 1 – 2 кН/м. Для определения горизонтального усилия на конце стрелы при работе механизма вращения приведенная к ее концу масса m_м принимается равной ml/3, где m – масса единицы длины стрелы (рис. 99, а). Для схемы, приведенной на рис. 99, б, из условия равенства кинематической энергии в процессе свободных колебаний равномерно распределенной массы стрелы m и приведенной к ее концу массы m_м находим, что

,

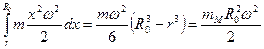где ω – угловая скорость вращения стрелы. Отсюда

m_м = .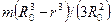

Эксплуатационные нагрузки и их расчетные комбинации зависят от типа крана и условий его эксплуатации и изучаются для кранов серийного производства.

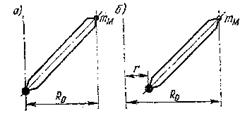
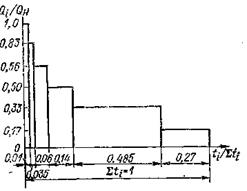
Рисунок 99 – Расчетные схемы стрел

На рис. 100 приведен шестиступенчатый график относительной величины нагрузки на крюке автомобильных кранов, которая регистрировалась аппаратурой без учета динамики, т.е. исключалось влияние типа привода и приемов работы крановщика. По данным этого графика, аналогично формуле (166), где Р_i = Q_i, а Р_Н = Q и вместо относительного числа циклов Z_i/ΣZ_i принято относительное время работы t_i/Σt_i, расчетная формула имеет вид

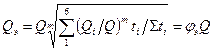
и коэффициенты эквивалентности φ_э имеют следующие значения: 0,44 при m = 3; 0,48 при m = 4 и 0,55 при m = 6. Полигоны распределения нагрузок на металлические конструкции стрел плавучих кранов в речных портах грузоподъемностью 10 и 15 т, полученные в эксплуатационных испытаниях, показали, что напряжения в стрелах распределяются по нормальным законам, величина среднего напряжения вызывается весом стрелы, а величина максимального напряжения (минимального напряжения) в цикле является суммой среднего напряжения и напряжений, вызываемых максимальными (минимальными) значениями внешних нагрузок.

Особенности расчета

Общие вопросы расчета сжатых и сжато-изогнутых элементов как призматического, так и переменного сечения по длине, а также расчеты безраскосных и пространственных ферм рассмотрены в л.11. Определению критической нагрузки при потере устойчивости крановых стрел в зависимости от переменности момента инерции сечения по длине в плоскости подвеса стрелы и в горизонтальной плоскости в условиях продольно-поперечного изгиба посвящена обширная литература. Кроме сложности таких расчетов они, к тому же, не в полной мере учитывают все обстоятельства работы стрел. Поэтому вместо проверки их устойчивости целесообразно проводить расчет их на прочность деформационным способом (см. л.11). При этом изгибающие моменты и поперечные силы в стреле, возникающие вследствие деформаций, надлежит определять как в плоскости подвеса, так и из плоскости подвеса. Для решетчатых стрел приходится определять их деформации, что значительно более трудоемко, чем определение деформаций балочных стрел, которые во многих случаях вычисляются по готовым формулам. Для определения прогибов ферм можно воспользоваться приемом, при котором прогиб фермы определяется как прогиб эквивалентной ей балки. Прогиб фермы определяется деформациями как поясов, так и решетки. Момент инерции фермы при рассмотрении ее как балки эквивалентной жесткости определяется исходя из равенства прогибов фермы и балки для данных условий закрепления и нагружения. Если момент инерции фермы определить как момент инерции ее поясов J_п, он будет преувеличен, а следовательно, прогиб преуменьшен. Преувеличение момента инерции будет тем больше, чем меньше жесткость решетки. С учетом деформации решетки момент инерции фермы J = J_п / µ, где µ > 1 – коэффициент, учитывающий влияние деформации решетки. Во многих случаях µ ≤ 1,1. Для стрелы с прямой осью наибольшее усилие сжатия в поясе

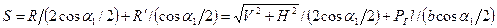
Влияние силы давления ветра на наветренную поверхность стрелы учитывается, как обычно. От действия веса стрелы возникает изгибающий момент, причем М_max= G₂lcos α/8. Влияние этого изгиба может быть значительно уменьшено моментом с обратным знаком М₀ = N'e, благодоря смещению оси подъемного блока в точку О₂ (рис. 101, г). Если подъемный канат пропустить через укрепленные на стреле кольца, чтобы он изгибался вместе со стрелой, натяжение каната не будет способствовать дополнительному изгибу стрелы. При а ≈ 0,2l в пролете и у точки крепления оттяжного каната к стреле О₁ расчетные значения изгибающих моментов будут одинаковы (рис.101, д). В плоскости подвеса влияние веса стрелы можно значительно снизить, прикладывая сжимающую силу R c эксцентриситетом е, т.е. ось стрелы сместить вверх на величину е по отношению к линии, соединяющей оси концевых блоков и нижних шарниров стрелы (рис.101, е). Если е = G₂l / (25R), поперечная нагрузка отвеса стрелы не будет влиять на величину критической силы и стрелу можно проверить на устойчивость без учета изгиба от ее веса, как центрально сжатый стержень.

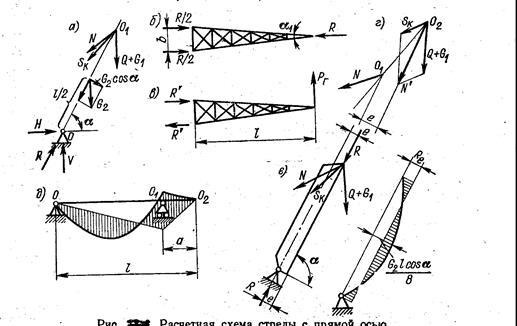
Рисунок 101 – Расчетная схема стрелы с прямой осью

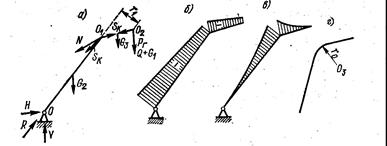
Рисунок 102 – Расчетная схема стрелы с изогнутой осью

Для стрелы с изогнутой осью (рис. 102, а) эпюры по длине стрелы сжимающих сил (рис. 102, б) и изгибающих моментов (рис. 102, в) приведены для случая, когда вес стрелы рассматривается как равномерно распределенная нагрузка. Наибольшее сжатие в корне стрелы вызывает реакция R на направление стрелы. Горизонтальная сила Р_г, перпендикулярная чертежу, приложенная в точке О₂ (рис. 102, а), кроме дополнительных усилий в поясах стрелы (см. рис. 101, в) вызывает кручение нижней части стрелы моментом М_кр = Р_г r₁(рис. 102, а), что является недостатком стрел этого типа. Для стрел с криволинейной осью (рис. 102, г)особен­ностью расчета являются определения напряжений в криволинейной части, которые должны выполняться по формулам для кривого бруса. При выборе направления подъемного каната вдоль стрелы надо иметь ввиду, что, если канат проходит ниже оси стрелы, усилие в канате уменьшает изгибающий момент в стреле от ее веса. Расчет стрел производится в нескольких положениях, в том числе при наибольшем и наименьшем вылетах. На устойчивость проверяется наиболее нагруженная ветвь стрелы. Проверка общей устой­чивости стрелы выполняется в пло­скости и из плоскости подвеса по схеме внецентренно сжатого стерж­ня с эксцентриситетом в плоскости подвеса, определяемым прогибом от веса стрелы, а из плоскости - про­гибом от сил инерции при повороте, от бокового ветра и наклона.

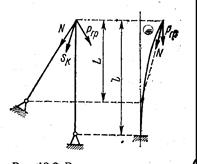
Рисунок 103 – Расчетная схема с учетом влияния оттяжки на устойчивость стрелы.

В плоскости подвеса расчетная длина стрелы определяется, как для стержня с двумя шарнирными кон­цами, а из плоскости, – как для стержня с одним заделанным, а другим свободным концом. В по­следнем случае влияние оттяжки улучшает условия устой­чивости стрелы. Когда конец стрелы выходит из плоскости подвеса, усилие в оттяжке N, ранее действовавшее в плоскости подвеса, становится наклонным к ней, отчего возникает составляющая усилия, препятствующая отклонению конца стрелы (рис. 103). Для расчета введем коэффициент k = Nl/(PL), где Р ≈ N + Р_гр– суммарная нагрузка на стрелу; N – усилие в оттяжном канате; Р_гр– усилие от груза. Коэффициенту k соответствуют следующие значения коэффициента приведения длины µ (см. л.11), для случая абсолютно жесткого основания мест закрепления стрелы и оттяжки.

Податливость мест закрепления снижает критическую нагрузку (при наличии оттяжки в меньшей степени, чем при ее отсутствии). Приведенные значения µ показывают, что принятие расчетной длины стрелы l_расч = 2l, как для стержня с одним заделанным и другим свободным концом, имеет место только при L = ∞, т. е. когда влияние оттяжки отсутствует. При k = 1 (l = L) l_расч = l, т. е. в обеих плоскостях стрела является стержнем с двумя шарнир­ными концами. Наконец, при L = 0 l_расч = 0,7 l и стрела в пло­скости, перпендикулярной к подвесу, является стержнем с одним заделанным, а другим шарнирным концом.

Расчет листовых стрел следует вести по материалам, приведен­ным в л. 11, пространственных решетчатых и безраскос­ных.

Литература: Основная: 6 [разд. 19: с.210÷219; разд.18: с. 203÷210].

Контрольные вопросы.

1. Назовите типы конструкций портальных кранов и приведите их основные параметры?

2. Дайте характеристику расчетным нагрузкам и их комбинациям для металлоконструкций портальных кранов?

3. В чем заключаются особенности расчета металлоконструкций портальных кранов?

4. Назовите типы конструкций металлоконструкций стреловых кранов?

5. Дайте характеристику расчетным нагрузкам и их комбинациям для металлоконструкций стреловых кранов?

6. Дайте характеристику расчетным нагрузкам и их комбинациям для металлоконструкций стреловых автомобильных кранов?

7. В чем заключаются особенности расчета металлоконструкций стреловых кранов?