Метод замены плоскостей проекций

Изменение взаимного положения проецируемой фигуры и плоскостей проекций методом перемены плоскостей проекций, достигается путем замены плоскостей П1 и П2 новыми плоскостями П4 (рис. 8.4). Новые плоскости выбираются перпендикулярно старым. Некоторые преобразования проекций требуют двойной замены плоскостей проекций (рис. 8.5). Последовательный переход от одной системы плоскостей проекций другой необходимо осуществлять, выполняя следующее правило: расстояние от новой проекции точки до новой оси должно равняться расстоянию от заменяемой проекции точки до заменяемой оси.

Задача 1: Определить натуральную величину отрезка АВ прямой общего положений (рис. 8.4). Из свойства параллельного проецирования известно, что отрезок проецируется на плоскость в натуральную величину, если он параллелен этой плоскости. Выберем новую плоскость проекций П4, параллельно отрезку АВ и перпендикулярно плоскости П1. Введением новой плоскости, переходим из системы плоскостей П1П2 в систему П1П4 , причем в новой системе плоскостей проекция отрезка А4В4 будет натуральной величиной отрезка АВ.

Рисунок 8.4. Определение натуральной величины отрезка прямой методом замены плоскостей проекций

Задача 2: Определить расстояние от точки C до прямой общего положения, заданной отрезком АВ (рис. 8.5).

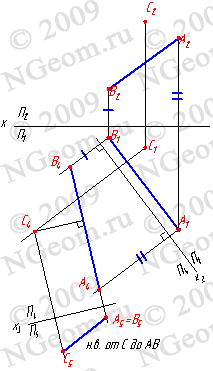
Рисунок 8.5. Определение натуральной величины отрезка прямой методом замены плоскостей проекций

ь объекту проецирования новые, частные по отношению к ним, положения.

№6

Поверхности вращения

Поверхность вращения общего вида образуется вращательным перемещением образующей линии вокруг неподвижной оси.

Каждая точка образующей линии при вращении вокруг неподвижной оси описывает окружность с центром на оси вращения. Эти окружности называются параллелями.

Наибольшую из параллелей (окружностей) поверхности вращения называют экватором поверхности, а наименьшую - горлом (шейкой) поверхности.

Плоскости, проходящие через ось поверхности вращения, называют меридиональными, а линии, по которым они пересекают поверхность, - меридианами. Меридиональная плоскость, параллельная плоскости проекции, называется плоскостью главного меридиана.

Линия пересечения плоскости главного меридиана с поверхностью вращения называется главным меридианом.

Пересечение поверхностей вращения плоскостью

При пересечении поверхности вращения плоскостью получается плоская фигура сечения. Построение проекций линии сечения необходимо начинать с определения опорных точек. К ним относятся точки, расположенные на очерковых образующих поверхности (точки, определяющие границы видимости проекций кривой), и точки, удаленные на экстремальные (максимальное и минимальное) расстояния от плоскостей проекций. После этого определяют произвольные (промежуточные) точки линии сечения.

Для определения точек, принадлежащих фигуре сечения, можно использовать различные методы. Один из них - метод вспомогательных секущих плоскостей. Суть его заключается в том, что заданные плоскость и поверхность вращения пересекают вспомогательной плоскостью. Находят линии пересечения этой плоскости с заданными плоскостью и поверхностью вращения. Затем отмечают точки, в которых пересекаются полученные линии пересечения. Построенные точки фигуры сечения соединяют плавной линией.

Развертки поверхностей вращения

Построение разверток поверхностей вращения имеет большое значение, особенно при конструировании из листового материала моделей различных сооружений, форм для металлических отливок, сосудов, трубопроводов, резервуаров и т.п.

Приближенные развертки

Поверхности, которые можно совместить с плоскостью без разрывов и складок, называют развертывающимися поверхностями. Фигуру, полученную при совмещении развертывающейся поверхности с плоскостью, называют разверткой.

Для развертывающихся поверхностей можно построить приближенную развертку.

При построении приближенной развертки поверхность аппроксимируют поверхностями вписанных или описанных многогранников, имеющих грани в форме прямоугольников или треугольников. Поэтому при графическом выполнении разверток поверхности всегда приходится производить разгибание или спрямление кривых линий, принадлежащих поверхности, что неизбежно приводит к потере точности.

Конус вращения

На виде сверху конус изображается кругом, являющимся одновременно горизонтальной проекцией основания конуса и его боковой поверхности (рис. 26). Центр круга – горизонтальная проекция вершины конуса. Главный вид и вид слева – равнобедренные треугольники.

Пусть в конусе имеется призматическое отверстие и точка А (А 2) лежит на линии пересечения конуса с отверстием.

Конус можно рассматривать как линейчатую поверхность, на которой точки могут быть построены с помощью прямолинейных образующих. Проекция А 1 точки А построена с помощью проекций l2 и l1 образующей l.

Сфера

Все проекции сферы – окружности. Диаметр их равен диаметру сферы. На каждом изображении проводят центровые линии.

На рис. 27 представлен чертёж сферы, усечённой двумя плоскостями, и показано построение точки А (А 1, А 2, А 3) на поверхности сферы.

Рис. 26. Конус вращения

Рис. 27. Сфера

Если рассматривать конус как поверхность вращения, то для решения задачи на построение точки интересно объединить его со сферой и тором.

В разновидностях аксонометрических проекций отсутствуют перспективные искажения, вследствие чего изображение получается условным и простым. Форму предмета можно строить точно по размерам (если нужно) и изображать ее «не как вижу, а как надо» с пониманием объективной сущности предмета. В этом заключается особенность технического рисунка и простота его выполнения, позволяющие сравнительно быстро приобрести необходимые навыки.

№9

Развертка поверхности цилиндра состоит из прямоугольника и двух кругов. Одну сторону прямоугольника берут равной высоте цилиндра, другую — длине окружности основания.

К прямоугольнику, пристраивают два круга, диаметр которых равен диаметру оснований цилиндра.

Развертка поверхности конуса представляет собой плоскую фигуру, состоящую из сектора — развертки боковой поверхности и круга — основания конуса.

Построение выполняется следующим образом:
1. Проводят осевую линию и из точки S, взятой на ней, описывают радиусом, равным длине S<4 образующей конуса, дугу окружности. На ней откладывают длину окружности основания конуса. Точку S соединяют с конечными точками дуги.
2. К полученной фигуре пристраивают круг. Диаметр этого круга равен диаметру основания конуса. Центр круга должен лежать на осевой линии так, чтобы круг касался дуги развертки боковой поверхности.

Длину окружности при построении p;i шерток цилиндра и мщусм можно определить по формуле С nD или графически. Для графического построения делят окружность на несколько частей, а затем откладывают их на прямой (для цилиндра) или на дуге окружности (для конуса).

№10