РАЗРЕЗЫ, ИХ ОТЛИЧИЕ ОТ СЕЧЕНИЙ, ВИДЫ РАЗРЕЗОВ

Внутреннее очертание полых предметов на черте­жах можно показать штриховыми линиями, но форма деталей часто требует значительного количества таких линий, которые пересекаясь с контурными и между собой, затрудняют понимание чертежа. Чтобы избежать этого яснее показать внутреннее устройство детали, применяют изображения, называемые разрезом. Разре­зом называется изображение предмета, мысленно рассечённого плоскостью или несколькими плоско­стями.

На разрезе показывается то, что получается в секу­щей плоскости я за ней. Иными словами, разрез состоит из сечения и изображения того, что расположено за се­кущей плоскостью.

Между разрезом и сечением существует различие. Его видно в рис. 20.

Разрез отличается от сечения тем, что на нём пока­зывают не только то, что находится в секущей плоско­сти, но и то, что наводится за ней.

При выполнении разрезов на чертежах:

1 Невидимые внутренние очертания, изображае­мые штриховыми линиями, обводят сплошными основ­ными линиями.

2. Сплошные основные линии, изображающие эле­менты детали, находящиеся на части детали, располо­женной перед секущей плоскостью, не проводят.

3. Фигура сечения, входящая в разрез, заштриховы­вается.

4. Мысленное рассечение предмета должно отно­сится только к данному разрезу и не влечёт за собой из­менения других изображений того же предмета.

Виды Разрезов

В зависимости от числа секущих плоскостей разре­зы разделяются на простые и сложные.

Простым называется разрез при одной секущей плоскости.

Сложным называется разрез при двух и более се­кущих плоскостях.

В зависимости от положения секущей плоскости относительно горизонтальной плоскости проекций, раз­резы подразделяют на вертикальные, горизонтальные и наклонные.

Вертикальным называется разрез при секущей плоскости, перпендикулярной горизонтальной плос­кости проекции.

Горизонтальным называется разрез при секущей плоскости, параллельной горизонтальной плоскости проекции.

Наклонным называется разрез при секущей плоскости, составляющий с горизонтальной плоско­стью проекции угол, отличный от прямого.

Вертикальный разрез при секущей плоскости параллельной фронтальной плоскости проекций на­зывается фронтальным разрезом.

Вертикальный разрез при секущей плоскости параллельной профильной плоскости проекций назы­вается профильным разрезом.

Местным разрезом называется разрез, служа­щий для выяснения устройства предмета лишь в от­дельном ограниченном месте.

Сечения

 

Производственные чертежи содержат различные типы изо­бражений — виды, разрезы, сечения. Сечения и разрезы позволяют выявить внешнюю и внутрен­нюю (рис. 147, а, б) форму детали. Названные изображения по­лучают в результате мысленного рассечения детали секущей плоскостью, положение которой выбирают в зависимости от формы изображаемой детали. Сечения и разрезы дополняют и уточняют геометрическую информацию о предмете и тем самым увеличивают возможности выявления формы изображаемого объекта на чертеже. В некоторых случаях они имеют большую информационную емкость, чем виды. Разрезы и сечения являют­ся проекционными изображениями и выполняются по правилам прямоугольного проецирования. Рис. 147. Сечение (а) и разрез (б)   Сечение — изображение фигуры, получающейся при мыслен­ном рассечении предмета секущей плоскостью. В сечении пока­зывается только то, что находится в секущей плоскости. Деталь проецируют на плоскость проекций V (рис. 148, а). Затем ее мысленно рассекают секущей плоскостью в том месте, где необходимо уточнить форму изделия. В секущей плоскости получают фигуру сечения. После этого секущую плоскость (вме­сте с фигурой сечения) мысленно вынимают, поворачивают во­круг вертикальной оси, перемещают параллельно плоскости про­екций и совмещают с плоскостью V так, чтобы изображения вида спереди и фигуры сечения не заслоняли друг друга (рис. 148, б). Обратите внимание на то, что при таком перемеще­нии секущей плоскости вид спереди находится в проекционной связи с сечением. Полученное изображение фигуры сечения на­зывают сечением, выполненным в проекционной связи. Секущую плоскость с фигурой сечения допускается переме­щать в произвольном направлении, совмещая ее с плоскостью проекций, без учета проекционной связи. Такое сечение называ­ется сечением, выполненным на свободном месте чертежа (рис. 148, в). Сечение можно располагать и на продолжении сле­да секущей плоскости (рис. 148, г). Оно называется сечением, выполненным на продолжении следа секущей плоскости. Если сечение располагается на продолжении следа секущей плоскости, то сечение не обозначается (см. рис. 148, г). Если се­чение располагается на свободном месте чертежа, то его обозна­чают надписью типа «А — А» (см. рис. 148, б, в). Если секущая плоскость проходит вдоль оси цилиндрической или фонической поверхности, ограничивающих отверстие или уг­лубление, то их контур на сечении показывают полностью, на­пример изображение углубления конической формы (см. рис. 148). Для выявления формы некоторых деталей иногда требуется выполнить несколько сечений, которые на чертеже обозначают буквами русского алфавита (рис. 149). ГОСТ 2.305—68 устанавливает правила изображения и обозначения сечений. Контуры фигуры сечения детали изображают сплошной ос­новной линией. Внутри этих контуров дают условное графическое обозначение материала детали (табл. 12). Рис. 148. Сечения: а — получение сечения; б - сечение, построенное в проекционной связи с видом; в - сечение, выполненное на свободном месте чертежа; г — се­чение, выполненное на продолжении следа секущей плоскости Рис. 149. Обозначение сечений буквами русского алфавита

 

№12

Особые случаи при построении разрезов

 

В технике часто можно встретить детали, содержащие такие конструктивные элементы, как тонкие стенки, ребра жесткости, спицы. При изображении их в разрезах приняты следующие правила: 1. Если секущая плоскость проходит вдоль тонкой стенки, ребра жесткости, спицы, то на разрезе их показывают нерассеченными (рис. 193). 2. Если секущая плоскость проходит поперек тонкой стенки, ребра жесткости, спицы, то на разрезе они показываются рассеченными (рис. 194).

 

№15

Изометрическая проекция Положение аксонометрических осей приведено на рис.1. Коэффициент искажения по осям x, y, z равен 0.82. Изометрическую проекцию для упрощения, как правило выполняют без искажения по осям x, y, z, т.е. приняв коэффициент искажения равным 1. Окружности, лежащие в плоскостях, параллельных плоскостям проекций, проецируются на аксонометрическую плоскость проекций в эллипсы (рис.2) Если аксонометрическую проекцию выполняют без искажения по осям x, y, z, то большая ось эллипсов 1,2, 3 равна 1,22, а малая ось - 0.71 диаметра окружности. Если аксонометрическую проекцию выполняют с искажением по осям x, y, z, то большая ось ось эллипсов 1, 2, 3 равна диаметру окружности, а малая - 0.58 диаметра окружности. Пример изометрической проекции детали приведен на рис. 3.

 

Рисунок 2. Окружность в изометрии 1-эллипс (большая ось расположена под углом 900 к оси y); 2-эллипс (большая ось расположена под углом 900к оси z); 3-эллипс (большая ось расположена под углом 900 к оси x).

Рисунок 3. Изометрическое изображение детали

 

Рисунок 4. Расположение аксонометрических осей прямоугольной диметрической проекции

Диметрическая проекция Положение аксонометрических осей приведено на рис.4. Коэффициент искажения по оси y равен 0.47, а по осям x и z - 0.94. Диметрическую проекцию, как правило, без искажения по осям x и z и с коэффициентом искажения 0.5 по оси y. Окружности, лежащие в плоскостях, параллельных плоскостям проекций, проецируются на аксонометрическую плоскость проекций в эллипсы (рис.5). Если димметрическую проекцию выполняют без искажения по осям x и z то большая ось эллипсов 1, 2, 3 равна 1,06 диаметра окружности, а малая ось эллипса 1 - 0.95, эллипсов 2 и 3 - 0.35 диаметра окружности. Если диметрическую проекцию выполняют с искажения по осям x и z, то большая ось эллипсов 1, 2, 3 равна диаметру окружности, а малая ось эллипса 1 - 0.9, эллипсов 2 и 3 - 0,33 диаметра окружности. Пример диметрической проекции детали приведен на рис.6.

 

Рисунок 5. Окружность в диметрии 1-эллипс (большая ось расположена под углом 900 к оси y); 2-эллипс (большая ось расположена под углом 900 к оси z); 3-эллипс (большая ось расположена под углом 900 к оси x).

Рисунок 6. Диметрическое изображение детали

 

Косоугольные проекции

Фронтальная изометрическая проекция

Горизонтальная изометрическая проекция

Фронтальная диметрическая проекция

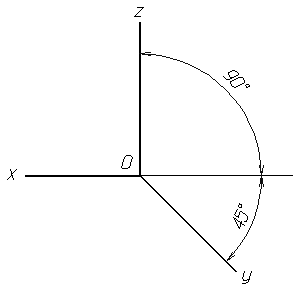Рисунок 7. Расположение аксонометрических осей фронтальной изометрической проекции

Фронтальная изометрическая проекция Положение аксонометрических осей приведено на рис. 7. Допускается применять фронтальные изометрические проекции с углом наклона оси у30 и 60°. Фронтальную изометрическую проекцию выполняют без искажения по осям х, у, z. Окружности, лежащие в плоскостях, параллельных фронтальной плоскости проекций, проецируются на аксонометрическую плоскость в окружности, а окружности, лежащие в плоскостях, параллельных горизонтальной и профильной плоскостям проекции, — в эллипсы (рис. 8). Большая ось эллипсов 2 и 3 равна 1,3, а малая ось — 0,54 диаметра окружности. Пример фронтальной изометрической проекции детали приведен на рис. 9.

 

Рисунок 8. Изображение окружности на фронтальной изометрической проекции 1-окружность; 2-эллипс (большая ось расположена под углом 22030/ к оси x); 3-эллипс (большая ось расположена под углом 22030/ к оси z).

Рисунок 9. Изображение детали на фронтальной изометрической проекции

 

Рисунок 10. Расположение аксонометрических осей горизонтальной изометрической проекции

Горизонтальная изометрическая проекция Положение аксонометрических осей приведено на рис. 10. Допускается применять горизонтальные изометрические проек­ции с углом наклона оси у 45 и 60°, сохраняя угол между осями х и у 90°. Горизонтальную изометрическую проекцию выполняют без искажения по осям х, у и z. Окружности, лежащие в плоскостях, параллельных гори­зонтальной плоскости проекций, проецируются на аксонометричес­кую плоскость проекций в окружности, а окружности лежащие в плоскостях, параллельных фронтальной и профильной плос­костям проекций— в эллипсы (рис. 11). Большая ось эллипса / равна 1,37, а малая ось — 0,37 диамет­ра окружности. Большая ось эллипса 3 равна 1,22, а малая ось — 0,71 диа­метра окружности. Пример горизонтальной изометрической проекции при­веден на рис. 12.

 

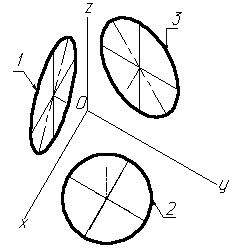Рисунок 11. Изображение окружности на горизонтальной изометрической проекции 1-эллипс (большая ось расположена под углом 150 к оси z); 2-окружность; 3.-эллипс (большая ось расположена под углом 300 к оси z)

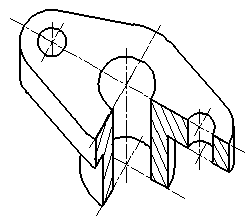Рисунок 12. Изображение детали на горизонтальной изометрической проекции

 

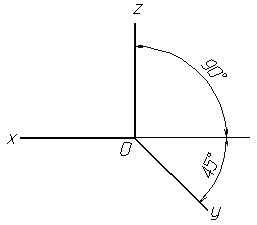Рисунок 13. Расположение аксонометрических осей фронтальной диметрической проекции

Фронтальная диметрическая проекция Положение аксонометрических осей приведено на рис. 13. Допускается применять фронтальные диметрические проекции с углом наклона оси у 30 и 60°. Коэффициент искажения по оси у равен 0,5, а по осям x и z-1. Окружности, лежащие в плоскостях, параллельных фрон­тальной плоскости проекций, проецируются на аксонометричес­кую плоскость проекций в окружности, а окружности, лежащие в плоскостях, параллельных горизонтальной и профильной плоскостям проекций, - в эллипсы (рис. 14). Большая ось эллипсов 2 и 3 равна 1,07, а малая ось - 0,33 диаметра окружности. Пример фронтальной диметрической проекции детали приведен на рис.15.

 

Рисунок 14. Изображение окружности на фронтальной диметрической проекции 1-окружность;2-эллипс (большая ось расположена под углом 7014/ к оси x); 3.-эллипс (большая ось расположена под углом 7014/ к оси z)

 

№16

Всякое изделие на чертеже вычерчивают в масшта­бе.

Масштабом называют отношение линейных размеров изображения предмета на чертеже к дейст­вительным размерам этого предмета.

Масштаб может быть выражен числом (числовой масштаб) или изображён графически - линейный мас­штаб. Числовой масштаб обозначают дробью, которая показывает кратность увеличения или уменьшения раз­меров изображения на чертеже. При выполнении черте­жей в зависимости от их назначения, сложности форм предметов и сооружений, их размеров применяют сле­дующие числовые масштабы, установленные ГОСТ 2.302-68.

Масштаб1:2;1:2,5-1:4;1:5;1:10;1:15;1:20;и т.д

уменьше­ния

Масштаб2:1;2,5:1;4:1;5:1;10:1;15:1;20:1;и т.д.

увеличе­ния

Натуральная величина1:1. Предпочтителен натуральный масштаб (М 1:1).Не предусмотренные стандар­том масштабы не применяют

№17

Уклон и Конусность

Иногда, в задачах по начертательной геометрии или работах по инженерной графике, или при выполнении других чертежей, требуется построить уклон и конус. В этой статье Вы узнаете о том, что такое уклон и конусность, как их построить, как правильно обозначить на чертеже.