Уравнение Шведова – Бингама

ЛЕКЦИЯ 4

Биореология

План лекции

Ньютоновские и неньютоновские жидкости. Уравнение Ньютона.

Динамическая и кажущаяся вязкость. Уравнение Шведова – Бингама.

Уравнение Бернулли.

Движение жидкости по трубам. Скорость течения.

Закон Пуазейля. Гидравлическое (периферическое) сопротивление.

Ламинарное и турбулентное течение. Число Рейнольдса.

Реологические свойства крови.

 

Ньютоновские и неньютоновские жидкости.

Уравнение Ньютона.

 

Реология – это раздел физики, изучающий силы сопротивления, возникающие в движущихся жидкостях и газах.

Жидкости не имеют своей формы. Они принимают всегда форму того сосуда, в котором они находятся. Основным параметром жидкости является её плотность r = m/V (кг\м³).

В жидкостях и в газах действует закон Паскаля: жидкости и газы передают давление во все стороны одинаково.То есть, если в какой-либо части объёма жидкости мы попытаемся повысить давление, то оно сразу распространится на весь объём жидкости. Величина давления измеряется в паскалях (Па) или Н\м². т.е. Р = F/S.

Представим себе, что внутри жидкости движется некоторая плоскость, причём, вектор её скорости направлен параллельно данной плоскости.

 

 

 

Слой жидкости, непосредственно прилегающий к этой плоскости, движется вместе с плоскостью с той же скоростью u. Отступив от плоскости на расстояние DY мы заметим, что скорость жидкости на этом расстоянии уменьшилась на величину Du . Таким образом, скорость слоёв жидкости уменьшается пропорционально увеличению расстояния от плоскости. Введём величину, которую назовём градиентом скорости:

 

grad u = Du/DY

 

Исаак Ньютон установил, что сила сопротивления, возникающая при движении тела в жидкости, пропорциональна градиенту скорости и величине плоскости:

 

F = -h(Du/DY)S

 

Это – уравнение Ньютона. Коэффициент h называется коэффициентом вязкости или динамической вязкостью. Он измеряется в Па . с .

Коэффициент вязкости у каждой жидкости имеет своё собственное значение.

Он также зависит от температуры жидкости и не зависит от скорости сдвига.

Те жидкости, которые подчиняются уравнению Ньютона, называются идеальными или ньютоновскими. К ним относятся такие жидкости, как вода, одноатомные спирты, эфир, бензин, керосин, минеральное масло, и др.

Однако существуют жидкости, которые не подчиняются уравнению Ньютона и при подсчёте силы сопротивления по формуле Ньютона получается большая погрешность. Такие жидкости в своём составе имеют либо высокомолекулярные соединения, либо представляют собой эмульсии, суспензии различных форменных элементов. Например, яичный белок сырого яйца, кисель, молоко и его продукты, кровь и т.д.Их вязкость значительно больше.

 

Динамическая и кажущаяся вязкость.

Уравнение Шведова – Бингама.

 

Для того, чтобы понять следующий раздел, вспомним один из видов деформации твёрдого тела: деформацию сдвига. Представим себе куб, сделанный из какого-либо твёрдого тела. Приложим к его верхней грани сдвигающую силу F. Отношение этой силы к величине площади верхней грани S называется сдвиговым напряжением (Н\м²) .

 

F/S=t- напряжение сдвига

 

dv/dx=g - градиент сдвиговой скорости.

 

Шведов и Бингам установили связь между сдвиговой скоростью и напряжением сдвига. Они вывели уравнение, которое носит их имя:

t = to + Mg

 

Здесь:

 

to - предел текучести, т.е. минимальное напряжение, при котором жидкость начинает течь. По аналогии с твёрдым телом, to- это такое сдвиговое напряжение, при котором тело перестаёт восстанавливать свою форму после снятия деформирующей нагрузки.

 

M - структурная вязкость. Она более полно отображает вязкость жидкостей. Например, при движении крови по сосудам, вязкость зависит не только от форменных элементов, но и от эластичности стенок сосуда.

 

При увеличении скорости движения жидкости структурная вязкость стремится к определённому пределу, который называется кажущейся вязкостью:

Графически изобразить уравнения Шведова – Бингама можно следующим графиком:

g

 

Следует отметить, что для ньютоновских жидкостей to равно нулю. Это значит, что в ньютоновских жидкостях сила трения покоя отсутствует полностью. Это можно обнаружить на таком примере. Предположим, что на поверхности абсолютно спокойной воды плавает какой-либо тяжёлый предмет (бревно). А вода является ньютоновской жидкостью, следовательно, плавающее тело можно привести в движение самой маленькой силой. Тоже бревно, лежащее на берегу, с места сдвинуть очень трудно, так как сила трения покоя при движении по поверхности твёрдого тела имеет значительную величину. Отсутствие в таких жидкостях силы трения покоя используется в точных навигационных приборах: компасах, гироскопах и пр. Следует добавить, что если ньютоновскую жидкость вылить на блюдце, то её поверхность сразу приобретает форму горизонтальной плоскости. С неньютоновской жидкостью наблюдается другая картина. Возьмём жидкость, являющуюся наиболее ярким представителем неньютоновских жидкостей: яичный белок. Если его вылить на блюдце, то его поверхность будет иметь форму небольшой горки, так как сила тяжести не в состоянии преодолеть до конца предел текучести жидкости.

Для очистки жидкостей от механических примесей используют фильтр из специальной пористой бумаги или ваты. Если нам приходится фильтровать воду, то мы заметим, что для фильтрации необходимо некоторое время. Если мы вместо воды возьмём спирт или бензин, то они через тот же фильтр будут профильтровываться быстрее, особенно бензин. Ведь чем меньше вязкость жидкости – тем быстрее она фильтруется. Надо сказать, что поддаются фильтрации все ньютоновские жидкости, даже такие, у которых высокая вязкость. Например, растительное масло будет тоже фильтроваться, но процесс фильтрации будет проходить медленно. А что будет, если мы попытаемся фильтровать неньютоновскую жидкость? Мы знаем, что наиболее ярким представителем ньютоновских жидкостей является яичный белок сырого яйца. Мы можем даже без практического опыта догадаться, что яичный белок вообще фильтроваться не будет, так как у него очень большой предел текучести. Не будут фильтроваться также и кисломолочные продукты. Строго говоря, все неньютоновские жидкости могут подвергаться процессу фильтрации, но для этого нужно их прогонять через фильтр действием дополнительной внешней силой. А силы тяжести для этого будет явно недостаточно.

 

Уравнение Бернулли

 

 

Рассмотрим движение идеальной жидкости по трубе произвольной формы и находящейся в произвольном положении.

 

 

Даниил Бернулли проанализировал движение жидкости по трубе и вывел уравнение, которое представляет собой закон превращения энергии для движущихся жидкостей. Для вывода данного уравнения, возьмём следующие узловые моменты. Во-первых учтём, что струя жидкости не разрывается, т.е. V1 = V2 (условие неразрывности струи. То есть: сколько жидкости втекает в трубу – столько и вытекает.

V1 = S1l1 V2 = S2l2

Согласно закону сохранения энергии, разность кинетических энергий струи на входе и на выходе равно работе внешних сил плюс разность потенциальных энергий на входе и на выходе.

Разность кинетических энергий:

DEk = mv2²/2 – mv1²/2 = (rS2l2v2² - rS1l1v1²)/2

Работа внешних сил – это работа сил давления:

Ap = F1l1 – F2l2 = p1S1l1 – p2S2l2

Работа силы тяжести – это разность потенциальных энергий:

Ag = DEp = mgh1 – mgh2 = rS1l1gh1 - rS2l2gh2

Согласно закону сохранения энергии, сумма работ внешних сил и силы тяжести равна изменению кинетической энергии:

Ap + Ag = DEk

или:

p1S1l1 – p2S2l2 + rS1l1gh1 - rS2l2gh2 = (rS2l2v2² - rS1l1v1²)/2

Данное выражение можно сократить, учитывая, что S1l1 = S2l2получим:

p1 –p2 + rgh1 -rgh2 = (rv2² - rv1²)/2

Произведём перегруппировку членов:

p1 + rgh1 + (rv1²)/2 = p2 + rgh2 + (rv2²)/2

Окончательно получим:

p + rgh + (rv²)/2 = const

Это и есть уравнение Бернулли.

В этом уравнении первое слагаемое – внешнее давление; второе слагаемое – гидростатическое давление; третье слагаемое – гидродинамическое давление, т.е.давление жидкости, вследствие её движения. Как следует из уравнения Бернулли, как бы жидкость ни текла, что бы мы с ней ни делали, по какой трубе мы бы её ни направляли, всегда сумма этих трёх величин будет иметь постоянное значение. Если одна из этих величие уменьшится, значит возрастут другие, но сумма их всё равно останется постоянной.

Возьмём трубу переменного сечения и пустим по ней жидкость.

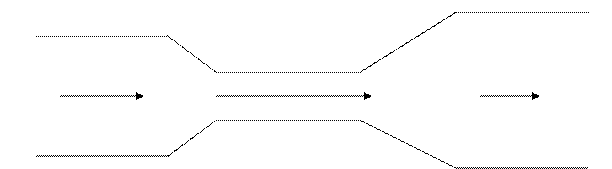
V1, p1 v2, p2 v3, p3

Согласно уравнению Бернулли, давление жидкости будет выше там, где скорость ниже и наоборот: где скорость выше, там будет давление ниже. На первый взгляд это противоречит здравому смыслу: как так: трубу сузили, а давление уменьшилось? И как насчёт закона Паскаля, не противоречит ли это ему? Но следует подчеркнуть, что закон Паскаля соблюдается только для неподвижных жидкостей, а в данном случае жидкость движется и поэтому, как следует из закона сохранения и превращения энергии, в суженной части, где скорость больше, давление должно быть меньше. Представим себе, что мы проделали сверху во всех участках этой трубы отверстия. Если бы жидкость была неподвижна, из всех отверстий били бы фонтанчики одной и той же высоты. Если бы жидкость была приведена в движение, то наблюдалась бы следующая картина: в широких частях трубы высота фонтанчиков бы увеличилась, а в узкой части – уменьшилась. При дальнейшем увеличении скорости жидкости высота фонтанчиков в узкой части трубы вообще уменьшилась бы до нуля, а при ещё большей скорости в этой части трубы давление стало бы ниже атмосферного и через это отверстие начал бы засасываться атмосферный воздух, т.е струя жидкости приобрела бы всасывающее действие.

Это явление используется на практике в пульверизаторе и в карбюраторе автомобильного двигателя. Это явление должны учитывать судоводители: когда суда идут параллельным курсом на небольшом расстоянии друг от друга, то возникает сила притяжения между ними. И если не принять соответствующие меры, суда могут стукнуться бортами и произойдёт авария. По этой же причине нельзя стоять рядом с быстро проходящим поездом: ведь проходящий поезд увлекает за собой огромную массу воздуха, а стоящий рядом человек создаёт между собой и поездом суженный канал, в котором, по закону Бернулли, создаётся пониженное давление и человек получает толчок в сторону поезда. А это может привести к несчастному случаю.