Корреляция и регрессия

Лекция

План:

1. Понятие о корреляции. Тиры корреляции.

2. Корреляционный коэффициент. Корреляционное отношение.

3. Регрессия.

4. Корреляция качественных признаков.

 

1. Корреляция означает связь, соотношение, сопряженность.

В природе существует 2 вида связи:

1 функциональная

2 корреляционная.

Функциональная связь - это такая связь, при которой каждому значению одной величине соответствует строго определённое единственное значение другой величины. (площадь круга - свой существующий радиус; скорость падения - ускорение ).

Корреляционная связь – это такая связь при которой среднему значению одной величины соответствует несколько значений другой величины.

Корреляционная связь бывает нескольких типов:

а) Связь может быть простая и множественная.

Простая корреляционная связь – это такая связь, когда исследования ведутся между двумя признаками:

Урожайность – предшественник

Урожайность – сорт

Урожайность – удобрение

Множественная корреляционная связь – это такая связь когда зависимость исследуется между тремя и более показателями:

Сорт

Урожайность - Предшественник

Удобрение

б) Связь может быть прямолинейная и криволинейная.

Прямолинейная связь - это такая связь , при которой с увеличением среднего значения одной величины – среднее значение другой величины увеличивается или с увеличением среднего значения одной величины среднее значение другой величины уменьшается.

Криволинейная связь – наблюдается когда с увеличением среднего значения одного признака – среднее значение другого признака сначала увеличивается, а потом уменьшается.

 

2.Корреляционный коэффициент. Корреляционное отношение.

 

Коэффициент корреляции r – указывает на силу связи и на направление связи. Изменяется коэффициент корреляции от -1 до +1 число указывает на силу связи, знак ( - , + ) на направление связи.

По значению r связь может быть:

Слабый – r от 0 до 0,33

Средняя – r от 0,33 до 0,66

Сильная – r от 0,66 до 0,99

Полная – r = 1

( + , - прямая, - , - обратная )

Коэффициент корреляции определяется по формуле

X , Y индивидуальное значение

¯x ¸¯y среднее

Коэффициент корреляции всегда определяется на основании выборки. Ошибка коэффициента корреляции рассчитывается по формуле

n- число пар

Коэффициент корреляции всегда записывается вместе со своей ошибкой

r ± Sr 0,73 ± 0,03.

Если число наблюдений n < 100 – то существенность корреляционной зависимости определяется по критерию t – стьюдента.

t теор. определяется при заданном уровне вероятности или значимости и числе свободы ν=n-2.

Если выборка большая n > 100, корреляционная связь будет существенная если отношение

далее вывод: связь считается существенной, если фактическое значение t ф ≥ t теор. Связь не существенная, если t ср < t теор. Квадрат коэффициента корреляции называется коэффициентом детерминации и обозначается .

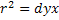
b y x – указывает на долю тех изменений, которые связаны с изучаемым признаком.

Коэффициент детерминации рассчитывается только при прямолинейной зависимости. При криволинейной зависимости рассчитывается корреляционное отношение от 0 до +1 – отрицательного значения не имеет. ζ – корреляционное отношение.

Если r = ζ – прямая зависимость.

Если ζ > r – криволинейная зависимость

 

3.Регрессия.

 

Регрессия – показывает количественное изменение результативного признака y ( функции ) по мере изменения независимого признака x ( аргумента ).коэффициент регрессии b показывает как изменяется одна величина по мере изменения другой величины на единицу изменения.

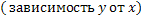
Регрессия может быть простая и множественная.

Регрессия также может быть прямолинейная и криволинейная.

Коэффициент регрессии рассчитывается:

 

Ошибка коэффициента регрессии рассчитывается:

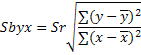
b – коэффициент регрессии

S b – ошибка регрессии

t теор – по таблице Стьюдента принятого уровня вероятности и числа степени свободы ν =n-2

4. Корреляция качественных признаков.

 

Расчет ведётся по формуле Юла:

Где частоты признаков с одинаковыми значениями

частота признаков с разными значениями

сумма частот по строкам

сумма частот по столбцам

В практике нередко возникает необходимость исследовать сопряжённость двух признаков у одних и тех же единицу наблюдения, когда один можно изменить ( количественный признак ), а в отношении другого только отметить его наличие или отсутствие ( качественный признак ) например: урожай картофеля вес с куста и пораженность фитофторой.

Коэффициент корреляции между качественными и количественными признаками вычисляют по формуле:

¯x – общее среднее значение для количественного признака

– среднее значение количественного признака с наличием качественного.

n – общее число всех наблюдений

– число случаев с наличием качественного признака.

S – общее стандартное отклонение для количественного признака.

( например: вычисляют существует ли связь между пораженностью фитофторой и урожайностью картофеля и какая связь?).