 |
Главная |
Алгоритм построения матрицы метрики графа
|
из
5.00
|
Исходные данные для построения матрицы метрики (отклонений):
1. Граф L=(X,U).
2. Матрица смежности R графа L c элементами логического типа:
ì 1, если вершины xi, xj – смежны;
ri,j = í
î0 в противном случае.
Введем обозначения:
R – матрица смежности заданного графа L;
E – единичная матрица;
М – матрица метрики (отклонений).
Описание алгоритма
Матрица метрики M= (mi,j) строится за несколько итераций по результатам последовательного возведения матрицы R=(E+R) в степень q=  до получения устойчивой матрицы Rk, где k – степень устойчивой матрицы Rk. Матрица Rk называется устойчивой, если Rk = Rk +1.
до получения устойчивой матрицы Rk, где k – степень устойчивой матрицы Rk. Матрица Rk называется устойчивой, если Rk = Rk +1.
Размерность матрицы М равна размерности матрицы R.
Все элементы матрицы М не определены.
Шаг 1.
Степень q матрицы R равна «1»: q=1.
" mi,i присваиваем значение «0», на основании аксиомы Фрише.
Шаг 2. Всем элементам mi,j, значения которых не определены, присвоить значение степени q, если соответствующие им элементы матрицы Rq ¹ 0. (Не забывайте, что значения элементов mi,j определяются только один раз).
Шаг 3. Проверяем, имеются ли в матрице M элементы mi,j, значения которых ещё не определены?
Если такие элементы имеются, то переходим к шагу 4; в противном случае – к шагу 7.
Шаг 4. Повышаем степень q матрицы R: q=q+1.
Шаг 5. Проверяем, является ли матрица Rq–1 устойчивой.
Если матрица Rq–1 – неустойчивая, то переходим к шагу 2.
Иначе – переходим к шагу 6.
Шаг 6. Всем элементам mi,j матрицы M, значения которых остались неопределенными, присваиваем значение ¥ (бесконечность). Это говорит о том, что граф L=(X,U) несвязный.
Шаг 7. Матрица метрики М=(mi,j) построена. Конец алгоритма.
Примечание: 1.*Элементам mi,j значения присваиваются только один раз! Следовательно, если элемент mi,j уже определён, то его значение не меняется*.
2. Радиус графа определяется по матрице метрики следующим способом: в каждой строке матрицы М выделяется максимальный элемент. Минимальный элемент из этих максимальных и есть радиус графа.
3. Диаметрграфа определяется по матрице метрики следующим способом: в каждой строке матрицы М выделяется максимальный элемент. Максимальный элемент из этих максимальных и есть диаметр графа.
Задание 6.
Произвести произвольно ориентацию рёбер графа G=(X,U) (рисунок 1) и для нового графа 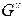 выполнить задания 1.1, 1.3, 5.
выполнить задания 1.1, 1.3, 5.
Задание 7.
Построить скелет графа 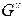 .
.
Скелет графа общего вида. В случае, когда при исследовании графа L=(X.U;P) общего вида требуется не полная информация о нём, а лишь знание того, какие пары его различных вершин смежны и какие нет, прибегают к носителю такой информации – скелету графа L, который обозначим как 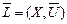 . Граф
. Граф  относится к классу обыкновенных графов с множеством вершин тем же, что и в графе L, и новым множеством рёбер
относится к классу обыкновенных графов с множеством вершин тем же, что и в графе L, и новым множеством рёбер  , определённым следующим образом:
, определённым следующим образом:
5) если в графе L есть петли, то они удаляются;
6) если в графе L есть дуги, то производится дезориентация дуг;
7) если в графе L есть кратные рёбра, то они заменяются одним эквивалентным ребром-звеном;
8) оставшиеся рёбра образуют множество рёбер  .
.
Таким образом, множество рёбер  состоит из рёбер, полученных из множества U после выполнения описанных выше процедур 1, 2, 3.
состоит из рёбер, полученных из множества U после выполнения описанных выше процедур 1, 2, 3.
Задание 8.
В графе G=(X,U) ( рисунок 1) найти все максимальные полные и максимальные пустые подграфы с помощью алгоритма Магу-Уэйсмана.
Структурный анализ графов
Определение: а)подграф называется максимальным пустым подграфом графа L=(X,U;P), если он не является подграфом никакого большего максимального пустого подграфа заданного графа;
б)подграф называется максимальным полным подграфом графа L=(X,U;P), если он не является подграфом никакого большего максимального полного подграфа заданного графа.
Легко доказать, что задача выявления максимальных полных (плотных) и максимальных пустых подграфов в заданном графе  общего вида легко сводится к случаю обыкновенных графов. Поэтому, для практического выявления всех максимальных полных и пустых подграфов в произвольном графе, достаточно уметь выявлять только максимальные плотные и пустые подграфы обыкновенных графов.
общего вида легко сводится к случаю обыкновенных графов. Поэтому, для практического выявления всех максимальных полных и пустых подграфов в произвольном графе, достаточно уметь выявлять только максимальные плотные и пустые подграфы обыкновенных графов.
Приведём алгоритм выявления всех максимальных пустых подграфов в заданном графе общего вида, основанный на работах Х. Магу и Дж. Уэйсмана:
п.1.Для графа L=(X,U;P) общего вида построим его скелет  ( смотри тему 1 данного методического пособия).
( смотри тему 1 данного методического пособия).
п.2. Построим матрицу инциденций А графа  , элементы которой ai,j принимают значения 0 либо 1 (
, элементы которой ai,j принимают значения 0 либо 1 (  ;
;  , где n =½X½ - число вершин в
, где n =½X½ - число вершин в  , m =½
, m =½  ½- число рёбер
½- число рёбер  в
в  ).
).
п.3. Дополним систему логическими переменными х1, х2, …, хi, …, хn , которые принимают значения 0 и 1, и подчиним её условиям:
 ;
;  ;
;  , 1+1=1, т.е. 2=1, (i=1,2,…,n),
, 1+1=1, т.е. 2=1, (i=1,2,…,n),
а также законам коммутативности, ассоциативности и дистрибутивности.
п.4. Из матрицы инциденций 
графа  , где n ,m соответственно равны числу вершин и рёбер графа, образуем матрицу
, где n ,m соответственно равны числу вершин и рёбер графа, образуем матрицу

и составим произведение
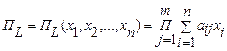
Очевидно, что j-й сомножитель произведения 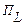 есть сумма двух слагаемых, соответствующих тем двум вершинам, которые в графе соединены j-м ребром.
есть сумма двух слагаемых, соответствующих тем двум вершинам, которые в графе соединены j-м ребром.
п.5. Преобразуем произведение 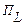 к бесскобочному виду и привести всю сумму к минимальной форме, пользуясь дистрибутивным, ассоциативным, коммутативным законами и применяя закон поглощения: а) а+ав =а; б) (а+в)(а+с)…(а+р) = =а+вс…р, где а,в,с,…,р - логические переменные, принимающие значения 0;1, выполняя при этом условия, описанные в п.3.
к бесскобочному виду и привести всю сумму к минимальной форме, пользуясь дистрибутивным, ассоциативным, коммутативным законами и применяя закон поглощения: а) а+ав =а; б) (а+в)(а+с)…(а+р) = =а+вс…р, где а,в,с,…,р - логические переменные, принимающие значения 0;1, выполняя при этом условия, описанные в п.3.
В результате выполненных преобразований выражение 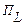 будет иметь минимальную форму и представлять сумму произведений переменных из множества х1, х2, …,хi,…,хn , т.е. многочлен. Обозначим его
будет иметь минимальную форму и представлять сумму произведений переменных из множества х1, х2, …,хi,…,хn , т.е. многочлен. Обозначим его  .
.
п.6. Для каждого слагаемого многочлена  выделим переменные, которые в него не входят, но входят в множество {х1, х2, …, хi, …, хn }. Эти переменные порождают максимальные пустые подграфы данного графа L, так как соответствующие им вершины графа L образуют максимальные пустые подграфы.
выделим переменные, которые в него не входят, но входят в множество {х1, х2, …, хi, …, хn }. Эти переменные порождают максимальные пустые подграфы данного графа L, так как соответствующие им вершины графа L образуют максимальные пустые подграфы.
ПРИМЕР. В графе 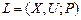 , представленном на рисунке 1, выделить все максимальные пустые подграфы.
, представленном на рисунке 1, выделить все максимальные пустые подграфы.

Матрица смежности B графа L содержит элементы (  ),
),  , равные:
, равные:
b11= b22= b33= b55=0; b44=1; b12=2; b13=1; b14 =0; b15 = 0;
b21=2; b23=0; b24 =2; b25 = 0; b31=1; b32=0; b34 =0; b35 = 3;
b41=0; b42=2; b43 =0; b45 = 1; b51=0; b52=0; b53 =3; b54 = 1;
ш.1. Строим скелет  (рисунок 2) графа
(рисунок 2) графа 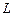 .
.

ш.2. Для графа  определим его матрицу инциденций А:
определим его матрицу инциденций А:
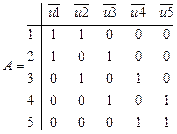
ш.3. Введём новые логические переменные х1, х2, х3, х4, х5 (по числу вершин в графе  ) и из матрицы А образуем матрицу Ах :
) и из матрицы А образуем матрицу Ах :
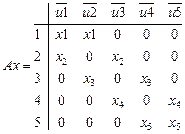
ш.4. Составляем произведение ПL
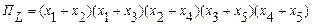
ш.5. Преобразуем выражения ПL к минимальной форме:
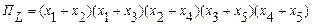 =
=
(перемножаем скобки первую со второй и третью с пятой)
=  =
=
(перемножаем скобки первую со второй)
 =
=
(перемножаем скобки первую со второй)

(применяем законы, указанные в п.п. 3,5 данного пособия)
= 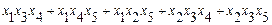 .
.
Преобразование выражения ПL закончено. Получена минимальная форма-полином  .
.
ш.6. Выделим для каждого слагаемого полинома
 =
= 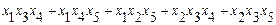
его дополнение до множества переменных {x1,x2, x3, x4, x5}:
(x2x5); (x2,x3); (x3,x4); (x1,x5); (x1,x4);
полученные дополнения порождают максимальные пустые подграфы графа 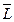 и заданного графа
и заданного графа 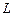 .
.
Алгоритм Х. Магу и Дж. Уэйсмана может быть применён и для выявления в графе L=(X,U; P) общего вида всех максимальных полных (плотных) подграфов. Для этого необходимо построить для заданного графа 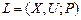 его скелет – граф
его скелет – граф  , а для графа
, а для графа  построить дополнительный граф
построить дополнительный граф  (определение дополнительного графа дано в теме 1 данного методического пособия). Получить дополнительный граф легко, если исходный граф задать матрицей смежности его вершин, в которой всем элементам, равным нулю, присвоить значение «1», а всем элементам, значения которых не равны нулю, присвоить значение «0».
(определение дополнительного графа дано в теме 1 данного методического пособия). Получить дополнительный граф легко, если исходный граф задать матрицей смежности его вершин, в которой всем элементам, равным нулю, присвоить значение «1», а всем элементам, значения которых не равны нулю, присвоить значение «0».
Далее для полученного графа  с помощью алгоритма Х. Магу и Дж. Уэйсмана (рассмотренного выше) выявляем все максимальные пустые подграфы. Эти подграфы являются максимальными полными (плотными) подграфами для графов
с помощью алгоритма Х. Магу и Дж. Уэйсмана (рассмотренного выше) выявляем все максимальные пустые подграфы. Эти подграфы являются максимальными полными (плотными) подграфами для графов  и
и 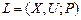 .
.
ПРИМЕР. В графе 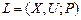 , представленном на рисунке 1, выделить все максимальные полные(плотные) подграфы.
, представленном на рисунке 1, выделить все максимальные полные(плотные) подграфы.
ш.1. Строим скелет  (рисунок 2) графа
(рисунок 2) графа 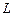 .
.
ш.2. Для графа  строим его дополнительный граф
строим его дополнительный граф  (рисунок 3), в котором с помощью алгоритма Х.Магу-Дж.Уэйсмана выявляем максимальные пустые подграфы.
(рисунок 3), в котором с помощью алгоритма Х.Магу-Дж.Уэйсмана выявляем максимальные пустые подграфы.

Приведём окончательный результат решения данной задачи - полином
 =
= 
и дополнения для его слагаемых: (  ); (
); (  ); (
); (  ); (
); (  ); (
); (  ), которые порождают все максимальные пустые подграфы графа
), которые порождают все максимальные пустые подграфы графа  и максимальные полные (плотные) подграфы графа
и максимальные полные (плотные) подграфы графа  и заданного графа
и заданного графа 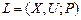 .
.
|
из
5.00
|
Обсуждение в статье: Алгоритм построения матрицы метрики графа |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

