Построение минимального остовного дерева

Лабораторная работа № 12

Тема: Экстремальные задачи на графах (продолжение)

Рассматриваемые вопросы:

- Задача о построении минимального остовного (порождающего) дерева

- Алгоритм Крускала

- Алгоритм Прима

1. Задача о построении минимального остовного (порождающего) дерева

Постановка задачи

Имеется n городов, которые нужно объединить в единую телефонную сеть. Для этого достаточно проложить (n-1) телефонных линий между городами. Как соединить города так, чтобы суммарная стоимость соединений (телефонного кабеля) была минимальна?

В общем случае, задачу можно сформулировать так. Пусть дан связный, неориентированный граф с весами на ребрах G(V, E), в котором V — множество вершин (контактов), а E — множество их возможных попарных соединений (ребер). Пусть для каждого ребра (u,v) однозначно определено некоторое вещественное число w(u,v) — его вес (длина или стоимость соединения). w() называется весовой функцией. Задача состоит в нахождении такого связного ациклического подграфа T ⊂ G, содержащего все вершины, что суммарный вес его ребер будет минимален.

Так как T связен и не содержит циклов, он является деревом и называется остовным, порождающим или покрывающим деревом (spanning tree). Остовное дерево T, у которого суммарный вес его ребер w(T) =∑_(u,v)∈T w(u,v) минимален, называется минимальным остовным, минимальным порождающим или минимальным покрывающим деревом (minimum spanning tree).

Рис. 1. Минимальное остовное дерево. Суммарный вес дерева равен 37. Это минимальное остовное дерево не уникально: удалением ребра (c,d) и добавлением ребра (a,b) получается новое минимальное остовное дерево.

Так как рассматриваются только деревья, можно считать все ребра положительными (достаточно добавить к весу всех ребер некоторую относительно большую положительную константу). В противном случае, если стоимость соединения между двумя вершинами равна отрицательному числу, можно несколько раз параллельно соединить их для уменьшения суммарного веса остовного подграфа.

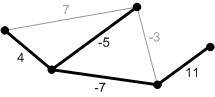
Рис.2-а. Минимальное остовное дерево. Суммарный вес равен 3.	Рис.2-б. Минимальный покрывающий подграф. Суммарный вес равен 0.

Также считаем, что для любой пары ребер их весовые характеристики будут различны. Это гарантирует уникальность построенного минимального остовного дерева. Для примера, если все ребра имеют единичный вес, то любое остовное дерево будет минимальным (с суммарным весом v-1, где v – количество вершин в графе).

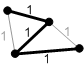
Рис.3. Все возможные минимальные остовные деревья для данного графа.

В данном случае, любой алгоритм построит одно из минимальных остовных деревьев. Один из вариантов разрешения неопределенности заключается в модификации алгоритма сравнения ребер по весу.

Области применения

· Разработка сетей. Ранее был приведен пример о соединении n городов в единую телефонную сеть с минимальной суммарной стоимостью соединений.

· Производство печатных плат. По аналогии с сетью: мы хотим соединить n контактов проводами с минимальной суммарной стоимостью. (Здесь стоит отметить, что задача о минимальном остовном дереве является упрощением реальности. В самом деле, если соединяемые контакты находятся в вершинах единичного квадрата, разрешается соединять любые его вершины, и вес соединения равен его длине, то минимальное покрывающее дерево будет состоять из трех сторон квадрата. Между тем все его четыре вершины можно электрически соединить двумя пересекающимися диагоналями, суммарная длина которых будет равна 2√2, что меньше 3 в первом случае).

· Минимальное остовное дерево может использоваться для визуализации многоаспектных, многомерных данных, например, для отображения их взаимосвязи (на картинке ниже продемонстрировано дерево схожести различных животных видов по размеру костей).

Рис.4. Минимальное остовное дерево может нагляднее представить эволюцию животных видов. С помощью него можно разбивать животных на группы и классы.

· Наука, и в частности биология, используют многомерные данные для группировки объектов, растений, животных. Минимальное остовное дерево позволяет разбивать их на взаимосвязанные классы, четко отслеживая близкие по строению и характеристикам группы.

Построение минимального остовного дерева

Найти минимальное остовное дерево в неориентированном нагруженном графе.