Алгоритм выделения минимального остовного дерева в неориентированном нагруженном графе G

1) Выберем в графе G ребро минимальной длины. Вместе с инцидентными ему двумя вершинами оно образует подграф G2 графа G. Положим I:=2.

2) Если I=N(G), то задача решена и G_i – искомое минимальное остовное дерево графа G. Иначе переходим к шагу 3).

3) Строим граф G_i+1. Для этого добавим к графу G_i новое ребро минимальной длины из оставшихся, которое инцидентно какой-либо вершине графа G_i и одновременно вершине, не содержащейся в G_i. Вместе с этим ребром включаем в G_i+1 и эту инцидентную ему вершину. Присваиваем I:=I+1 и переходим к шагу 2).

Пример 1.

Найдем минимальное остовное дерево в неориентированном нагруженном графе, изображенном на рис.5.

Рис.5.

Обозначим ребро, соединяющее вершины Vi и Vj через Xij.

Для удобства использования приведенного выше алгоритма решения поставленной задачи, составим матрицу длин ребер. В рассматриваемом графе количество вершин N=8, следовательно, матрица длин ребер графа G Будет иметь размерность 8×8 и выглядеть следующим образом:

Согласно приведенному выше алгоритму, выбираем ребро минимальной длины (выбираем среди элементов матрицы C(G), минимальное − это C₄₇=1) и вместе с инцидентными ему двумя вершинами относим к графу G₂. Таким образом, . Длина дерева G₂ будет равна L(G₂)=C₄₇=1. Поскольку , продолжаем работу алгоритма.

По четвертой и седьмой строкам ищем минимальное число (за исключением использованной единицы) − ребро минимальной длины, инцидентное либо вершине V₄, либо V₇. Выбираем ребро X₄₆ с длиной C₄₆=3 и вместе с вершиной V₆ добавляем к графу G₂, обозначая его теперь как G₃: , при этом L(G₃)=C₄₇+C₄₆=1+3=4. Аналогично находим графы:

, ;

, ;

,

;

,

;

,

.

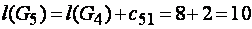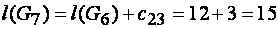Поскольку I=8=N(G), работа алгоритма заканчивается.

Таким образом, искомое минимальное остовное дерево графа G − граф G₈, изображенный на рис. 6, длина которого равна 22.

Рис.6

Определение. Безопасным ребром e относительно некоторой компоненты связности К из А назовем ребро с минимальным весом, ровно один конец которого лежит в К.

2. Алгоритм Крускала

 

Алгоритм Крускала— алгоритм построения минимального остовного дерева взвешенного связного неориентированного графа. Алгоритм впервые описан Джозефом Крускалом (Kruskal) в 1956 году.

Алгоритм Крускала объединяет вершины графа в несколько связных компонент, каждая из которых является деревом. На каждом шаге из всех ребер, соединяющих вершины из различных компонент связности, выбирается ребро с наименьшим весом. Необходимо проверить, что оно является безопасным. Так как ребро является самым легким из всех ребер, выходящих из данной компоненты, оно будет безопасным.

Остается понять, как реализовать выбор безопасного ребра на каждом шаге. Для этого в алгоритме Крускала все ребра графа G перебираются по возрастанию веса. Для очередного ребра проверяется, не лежат ли концы ребра в разных компонентах связности, и если это так, ребро добавляется, и компоненты объединяются.

Удобно использовать для хранения компонент структуры данных для непересекающихся множеств, как, например, списки или, что лучше, лес непересекающихся множеств со сжатием путей и объединением по рангу (один из самых быстрых известных методов). Элементами множеств являются вершины графа, каждое множество содержит вершины одной связной компоненты. Для работы с множествами используются следующие процедуры:

Make-Set(v)	Создание множества из набора вершин
Find-Set(v)	Возвращает множество, содержащее данную вершину
Union(u,v)	Объединяет множества, содержащие данные вершины

Общая схема алгоритма выглядит так:

MST_Kruskal(G,w)

1 A «- пустое множество

2 for (Для) каждой вершины v є V[G]

3 do Make_Set(v)

4 Сортируем ребра из Е в неубывающем порядке их весов w

5 for (Для) каждого (u, v) G Е (в порядке возрастания веса)

6 do if Find_Set(u) != Find_Set(v)

7 then A «- A объединить с {(u, v)}

8 Union(u, v)

9 return A

В строках 1-3 выполняется инициализация множества А пустым множеством и создается |V| деревьев, каждое из которых содержит по одной вершине.

Ребра в Е в строке 4 сортируются согласно их весу в неубывающем порядке.

Цикл for в строках 5-8 проверяет для каждого ребра (u, v), принадлежат ли его концы одному и тому же дереву. Если это так, то данное ребро не может быть добавлено к лесу без того, чтобы создать при этом цикл, поэтому в таком случае ребро отбрасывается.

В противном случае, когда концы ребра принадлежат разным деревьям, в строке 7 ребро (и, v) добавляется в множество А, и вершины двух деревьев объединяются в строке 8.

Время работы алгоритма Крускала для графа G = (V, Е) зависит от реализации структуры данных для непересекающихся множеств. Время работы алгоритма Крускала можно записать как О (Е * lg V).

Пример 2. Выполнение алгоритма Крускала.

 

1. Начальная фаза. Минимальный покрывающий лес пуст.

2. Перебираем ребра в порядке возрастания веса: первое ребро с весом 2. Добавляем его к А.

3. Следующее безопасное ребро с весом 6. Добавляем его.

4-8. Добавляем остальные безопасные ребра.

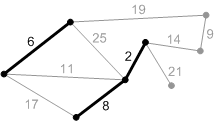
Ребра с весом 17, 19 и 25 – не безопасные. Их концы лежат в одной компоненте связности. Ребро с весом 21 – безопасное, поэтому добавляем его. Минимальное остовное дерево построено.

3. Алгоритм Прима

Как и алгоритм Крускала, алгоритм Прима следует общей схеме алгоритма построения минимального остовного дерева: на каждом шаге мы добавляем к строящемуся остову безопасное ребро.

Алгоритм впервые был открыт в 1930 году чешским математиком Войцехом Ярником, позже переоткрыт Робертом Примом в 1957 году, и, независимо от них, Э. Дейкстрой в 1959 году.

Алгоритм Прима обладает тем свойством, что ребра в множестве А всегда образуют единое дерево. Дерево начинается с произвольной корневой вершины г и растет до тех пор, пока не охватит все вершины в V. На каждом шаге к дереву А добавляется легкое ребро, соединяющее дерево и отдельную вершину из оставшейся части графа. Данное правило добавляет только безопасные для А ребра; следовательно, по завершении алгоритма ребра в А образуют минимальное остовное дерево. Данная стратегия является жадной, поскольку на каждом шаге к дереву добавляется ребро, которое вносит минимально возможный вклад в общий вес.

В качестве входных данных алгоритму передаются связный граф G и корень r минимального остовного дерева. Все вершины G, еще не попавшие в дерево, хранятся в очереди с приоритетом Q. Приоритет вершины v определяется значением key[v], которое равно минимальному весу ребер, соединяющих v с вершинами минимального остова. Поле prev[v] для вершин дерева указывает на родителя, а для вершин из очереди указывает на вершину дерева, в которую ведет ребро с весом key[v] (одно из таких ребер, если их несколько).

 

 

Алгоритм Прима выглядит следующим образом:

MST-PRIM(G,w, r)
1: Ω ← V[G]
2: foreach (для каждой) вершины u ∈ Ω
3: do key[u] ← ∞
4: key[r] ← 0
5: p[r] = NIL
6: while (пока) Ω ≠ 0
7: do u ← EXTRACT-MIN(Ω)
8: foreach (для каждой) вершины v ∈ Adj(u)
9: do if v ∈ Ω и w(u,v) < key[v] then
10: p[v] ← u
11: key[v] ← w(u,v)

 

В строках 1-5 ключи всех вершин устанавливаются равными INFINITY (за исключением корня r, ключ которого равен 0, так что он оказывается первой обрабатываемой вершиной), указателям на родителей для всех узлов присваиваются значения NIL и все вершины вносятся в очередь с приоритетами Q. Алгоритм поддерживает следующий инвариант цикла, состоящий из трех частей.

Перед каждой итерацией цикла while в строках 6-11

A={(v,prev[v]):v є V - {r} - Q};
вершины, уже помещенные в минимальное остовное дерево, принадлежат множеству V — Q;
для всех вершин v є Q справедливо следующее:

если prev[v] != NIL, то key [v] < INFINITY и key [v] — вес легкого ребра (v,p[v]), соединяющего v с некоторой вершиной, уже находящейся в минимальном остовном дереве.

4. В строке 7 определяется вершина u, принадлежащая легкому ребру, пересекающему разрез (V — Q,Q) (за исключением первой итерации, когда и = r в соответствии с присвоением в строке 4). Удаление и из множества Q добавляет его в множество V — Q вершин дерева.

Цикл for в строках 8-11 обновляет поля key и prev для каждой вершины v, смежной с u и не находящейся в дереве. Это обновление сохраняет третью часть инварианта.

 

Пример 3. Выполнение алгоритма Прима.

1. Начальная фаза. Минимальный покрывающий лес состоит из корня r и пустого множества ребер.

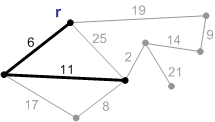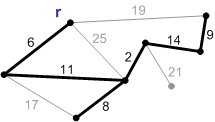
2. Ребро с весом 6 является минимальным ребром, соединяющим корень с остальными вершинами. Добавляем его к минимальному остову.   3. Следующее безопасное ребро с весом 11. Добавляем его. 4-8. Добавляем остальные безопасные ребра   Ребра с весом 17, 19 и 25 – не безопасные. Их концы лежат в одной компоненте связности. Ребро с весом 21 – безопасное, поэтому добавляем его. Минимальное остовное дерево построено.

Время работы алгоритма Прима O(ElogV).

Задание 1. Постройте остовное дерево минимального веса, используя алгоритмы Прима и Крускала. Подсчитайте вес дерева.

Задание 2. Имеется 7 городов А₁, А₂, A₃, А₄, A₅, A₆, А₇, которые нужно связать между собой наиболее дешевой сетью дорог, если известно, что стоимость C(A_i А_к) сооружения участка дороги, соединяющей города А_i и А_к (i, к = 1, 7), пропорциональна ее длине.

 

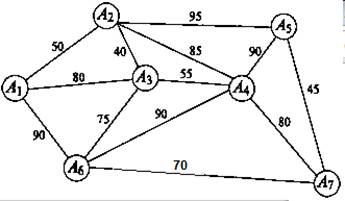
Постройте минимальное остовное дерево, используя алгоритмы Прима и Крускала. Определите минимальную стоимость сети дорог.