 |
Главная |
Скопируйте исходные данные на новый лист в ячейки A1:D14
|
из
5.00
|
2. Выделите диапазон ячеек B17:E21 (рис.2) для сохранения результатов вычислений функции ЛИНЕЙН – массива регрессионной статистики.
Функция ЛИНЕЙН рассчитывает статистику для ряда с применением метода наименьших квадратов.
3. Вызовите статистическую функцию ЛИНЕЙН и установите параметры, как на рис.1. Параметр Изв_знач_y содержит диапазон D2:D14, т.е. известные значения y. Параметр Изв_знач_х содержит диапазон A2:C14, т.е. известные значения х. Параметр Стат=1 – для получения дополнительной статистики.

Рис. 1
4. После нажатия ОК встаньте на строку формул (или нажмите F2) и нажмите Ctrl+Shift+Enter. В результате должен получиться массив значений, показанный на рис.2.
На рисунке искомые коэффициенты a0, a1, a2, a3 выделены (подробнее см. справку F1). Коэффициент детерминации R2=0.9725 вполне удовлетворителен (близок к единице).
Таким образом, аппроксимирующая формула y=a0+a1x1+a2x2+a3x3 имеет вид:
Y = –19,27 + 1,36*х1 + 0,1*х2 – 0,21*х3

Рис. 2
5. С использованием полученной формулы вычислите теоретические значения yтеор и прогнозное значение функции yпрогн при х1 = 37, х2 = 11, х3 = 3, записав самостоятельно в любую ячейку формулу для расчета. Результат расчета: yпрогн= 31,63.
Для этой же задачи рассмотрите пример использования функции ТЕНДЕНЦИЯ для расчета значений y при других различных вариантах данных X.
Справка: функция ТЕНДЕНЦИЯ лишь вычисляет значения аппроксимирующей функции в диапазоне наблюдения без предоставления ее характеристик.
| Новые значения X | ||
| x1 | x2 | x3 |
| 8,5 | ||
| 8,5 | ||
Порядок решения задачи:
1. Новые значения Х, для которых надо рассчитать y, введите в ячейки F2:H14.
2. Выделите диапазон I2:I14 для записи в него рассчитываемых значений y.
3. Вызовите функцию ТЕНДЕНЦИЯ. Параметры функции заполните как на рис.3. Параметр Нов_знач_х содержит диапазон F2:H14, т.е. новые значения x.

Рис. 3
После нажатия ОК встаньте на строку формул (или нажмите клавишу F2) и нажмите Ctrl+Shift+Enter. В результате диапазон I2:I14 будет заполнен рассчитанными значениями y (рис.4).
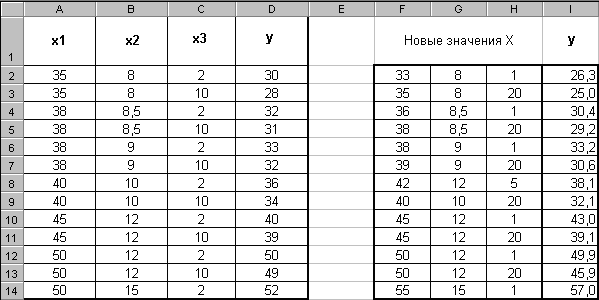
Рис. 4
6. Оценка эффективности рекламы. Прогнозирование с использованием функций ЛГРФПРИБЛ и РОСТ
Экспериментально известны проценты увеличения оборота при затратах в 5, 10, 15, 20 тыс.$ в 3-х масс-медиа – на телевидении, радио и в прессе:
| 5 тыс. $ | 10 тыс. $ | 15 тыс. $ | 20 тыс. $ | |
| 1. TV | 28% | 43% | 61% | 95% |
| 2. Радио | 15% | 24% | 34% | 50% |
| 3. Пресса | 6% | 9% | 13% | 20% |
Подберите формулу для вычисления процента увеличения оборота при различных затратах на рекламу.
Кроме этого, надо вычислить процент увеличения оборота при затратах на рекламу в прессе 2 тыс.$ и на телевидении 22 тыс.$. Дополнительно вычислите проценты при затратах во всех масс-медиа 2, 17 и 25 тыс.$.
Решение задачи. Для решения задачи в первую очередь правильно разместите данные (рис.1).

Рис. 1
Вычислите массив с регрессионной статистикой функцией ЛИНЕЙН: выделите диапазон ячеек F2:H6 и проделайте известные из предыдущего примера (п.5) действия. В итоге должен получиться массив:
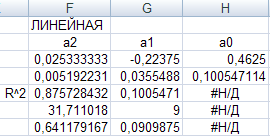
Видно, что коэффициент детерминации R2=0.8757 недостаточно удовлетворителен.
Поэтому выполните подбор формулы с помощью функции для нелинейных зависимостей ЛГРФПРИБЛ.
Справка: функции ЛГРФПРИБЛ и РОСТ применяют для аппроксимации экспериментальных данных нелинейные (показательные) зависимости вида 
Функция ЛГРФПРИБЛ (как и функция ЛИНЕЙН) возвращает массив с вычисленными значениями параметров (a0, a1, a2, …, an), коэффициентом детерминации R2 и другими характеристиками функции.
|
из
5.00
|
Обсуждение в статье: Скопируйте исходные данные на новый лист в ячейки A1:D14 |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

