Связь магнитного момента с механическим моментом количества движения атома

Электрон, движущийся по орбите, наряду с механическим моментом количества движения обладает также магнитным моментом. Движение электрона по орбите эквивалентно контуру с током, поэтому он возбуждает в окружающем пространстве магнитное поле, равное полю магнита с моментом 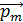, равным:

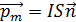(2.1)

где I — сила тока в контуре, S — площадь контура, 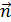— единичный вектор нормали к плоскости контура. Направление магнитного момента обычно находится по правилу буравчика: если вращать ручку буравчика в направлении тока, то направление магнитного момента будет совпадать с направлением поступательного движения буравчика.

Двигаясь по круговой орбите радиуса r со скоростью υ, частица с зарядом q совершает один оборот за время 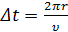, и создает эффективный круговой ток рис. 1.1:

 

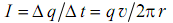
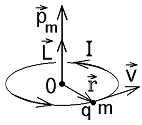
Площадь такого тока S=πr² , а создаваемый им магнитный момент, согласно (2.1), по модулю равен:

 

Рис.1.1

 

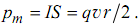
С учетом направления векторов, указанных на рис.1.1, движущаяся заряженная частица обладает магнитным моментом:

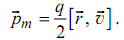
(2.2)

Эта формула справедлива не только для круговой, но и для любой другой траектории частицы. Если учесть, что момент импульса частицы:

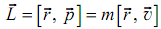
то оказывается, что магнитный момент и момент импульса движущейся заряженной частицы связаны соотношением:

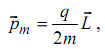
(2.3)

- гиромагнитное отношение.

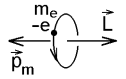
Рис.1.2

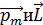На рис. 1.2 изображено движение положительно заряженной частицы. Заряд электрона q = – e отрицателен, и для электрона с массой m_e векторы направлены в противоположные стороны (рис. 1.2).

Намагничивание среды может происходить при появлении элементарных токов намагничивания, созданных движением электронов. При сложении магнитных моментов отдельных электронов, согласно формуле (2.3), складываются и моменты их импульсов:

 

 

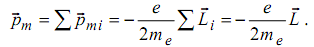
Гиромагнитное отношение справедливо не только для отдельного электрона, но и для всего намагниченного образца в целом.

Полученная формула (2.3) говорит о том, что магнитный момент заряженной микрочастицы будет квантоваться вместе с ее моментом импульса. Для электрона:

 

 

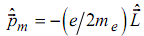
Если ввести постоянную:

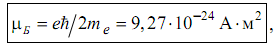
(2.4)

 

называемую магнетоном Бора (e и m_e – заряд и масса электрона), то с учетом формул таблицы 1, получаем дискретный спектр разрешенных значений величины магнитного момента и его проекции на выделенную ось z для движущегося электрона:

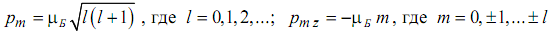
(2.5)

 

Магнетон Бора – это квант магнитного момента.

Кроме орбитального момента количества движения L электрон обладает также собственным моментом количества движения (спином) S=L_s:

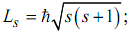
(2.6)

 

где - спин электрона.

В отличие от целых квантовых чисел l и m, спиновое число s может быть как целым, так и полуцелым. Для фотона s = 1; для электрона, протона, нейтрона .

Электрон, обладающий спином, должен вести себя как магнит и, следовательно, должен обладать спиновым магнитным моментом 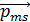, но гиромагнитное отношение для него аномально, оно в два раза больше отношения (2.3).

 

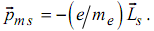(2.7)

 

С учетом (2.6), (2.7) и (2.4) формулы квантования собственного магнитного момента электрона имеют вид:

 

 

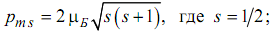
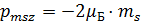
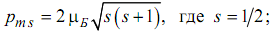
(2.8)