Построение регрессионной модели (определение функции «черного ящика»)

Регрессионные модели. Аппроксимация данных. Подбор формул со многими неизвестными

Построение регрессионной модели (определение функции «черного ящика»)

Задача. Известны данные динамики выпуска продукции предприятия за 10 лет (набор из n=10 экспериментальных точек):

X
Y

X – порядковый номер года с 2001 по 2010; Y – объем валовой продукции предприятия.

Выполним регрессионный анализ, то есть, опираясь на имеющиеся экспериментальные данные, построим регрессионную модель (определим функцию черного ящика), по которой вход преобразуется в выход.

Схема одномерной регрессионной модели

Экспериментальные точки отображены на графике:

График экспериментальных данных

Занесите экспериментальные данные в таблицу Excel:

Xi	Yi

Результат ввода данных:

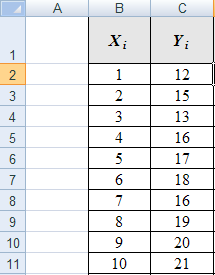
Предположим, что экспериментальные данные подчиняются линейному закону, т.е. выдвигаем гипотезу о линейной модели: Y = aX + b.

Построение модели выполним по методу наименьших квадратов, суть которого в том, что необходимо найти такие значения коэффициентов a и b, при которых сумма квадратов отклонений F экспериментальных данных от расчетных (теоретических) значений Y будет минимальной:

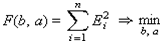
Здесь: E_i – ошибки между экспериментальными данными и расчетными значениями Y; F – суммарная ошибка (сумма квадратов отклонений).

Уравнения для E_i и F имеют вид:

E_i = (Y_i^Эксп. – Y_i^Теор.) = Y_i – b – aX_i, i = 1, …, n.

Для определения значений b и a, которые доставляют экстремум функции F, находятся частные производные по переменным b и a и приравниваются к нулю (условие экстремума):

После раскрытия скобок получится система линейных уравнений:

Для ее решения составьте в Excel таблицу промежуточных вычислений, используя соответствующие формулы и функцию СУММ:

	Xi	Yi	Xi2	XiYi
Сумма:

Результат ввода

Полученная система линейных уравнений в матричной форме имеет вид:

Подстановка из таблицы соответствующих значений сумм при решении системы «вручную» дает:

Существуют следующие способы решения системы линейных уравнений (определения коэффициентов b и a):

- методом Крамера;

- методом Гаусса;

- методом обращения начальной матрицы.

При решении системы методом Крамера получаются следующие выражения для b и a:

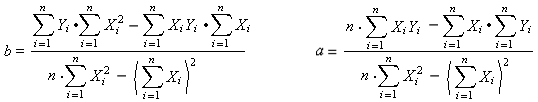
Введите данное решение в таблицу Excel:

- для коэффициента b:

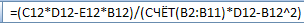
- для коэффициента a:

Здесь для вычисления общего числа точек n использована функция СЧЁТ.

 

Найдем значения b и a «ручным» способом:

Удостоверьтесь, что полученные с помощью Excel и «вручную» значения b и a совпадают.

 

Существует также способ определения коэффициентов b и a с использованием расчетных формул, представленных в развернутом (скалярном) виде:

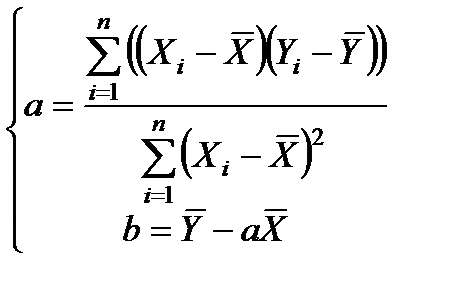
где 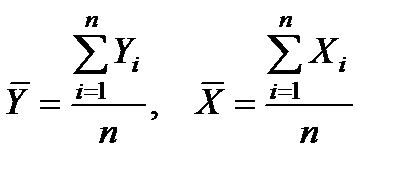– средние значения Y и X (в Excel реализуется функцией СРЗНАЧ).

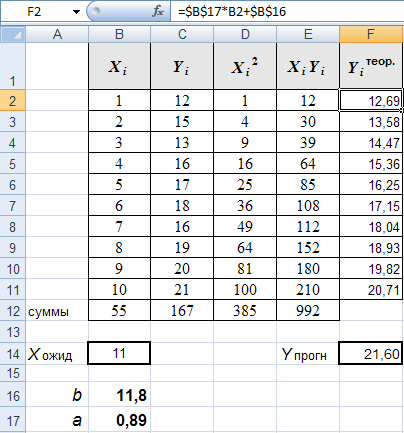
Решение задачи данным способом выполните на самостоятельной подготовке. Таблица Excel с расчетами этим способом имеет вид:

 

Итак, найденные значения b = 11.8 и a = 0.89 обеспечивают прохождение графика Y = aX + b как можно ближе одновременно ко всем экспериментальным точкам. Таким образом, получено линейное уравнение: Y = 0.89X + 11.8.

Произведите расчеты теоретических (эмпирических) значений Y_i^теор. по данной линейной функции. Для расчетов используйте абсолютные ссылки (знак $) на ячейки с полученными значениями b и a.

Для ожидаемого значения X_ож=11 (на 11-й год) определите прогнозное значение Y(X_ож=11).

Теперь необходимо проверить правомерность принятой гипотезы о полученной линейной зависимости Y = 0.89X + 11.8.

Для этого необходимо рассчитать ошибку E_i между экспериментальными точками Y и точками полученной теоретической зависимости Y^теор., суммарную ошибку F, значение стандартного отклонения σ и вероятного отклонения S по формулам:

E_i = Y_i – b – aX_i, i = 1, …, n

Значение S связано с σ соотношением:

S = σ/sinβ = σ/sin(90°–arctga) = σ/cos(arctga).

 

Такая зависимость между S и σ получена из рисунка:

Рис. Связь σ и S

Для проверки правильности принятия гипотезы используется нормальный закон распределения случайных ошибок. На рисунке P – вероятность распределения ошибки.

Рис. Иллюстрация закона нормального распределения ошибок

Если в полосу, ограниченную линиями Y^теор-S = aX+b-S и Y^теор+S = aX+b+S попадет 68.26% или более из всех экспериментальных точек, то можно сделать вывод о том, что принятая гипотеза о линейной зависимости Y = aX + b верна.

 

 

Создайте таблицу для расчетов ошибок между точками экспериментальной и теоретической зависимости:

Примечание: формулы последнего столбца L реализованы с использованием функций ЕСЛИ и И.

Значение суммарной ошибки будет F = 10.62

Значение .

Значение S = σ/cos(arctg(a)) = 1.38.

Таблица результатов создания регрессионной линейной модели:

 

 

Расчеты показывают, что 7 точек из 10 (то есть 70%) попадают в полосу, ограниченную линиями Y_нижняя = 0.89X + 11.8 – 1.38 и Y_{верхняя} = 0.89X + 11.8 + 1.38, из чего заключаем: зависимость между входом и выходом модели линейная, то есть выдвинутая гипотеза о линейной зависимости верна.

 

Проиллюстрируем расчеты на графике:

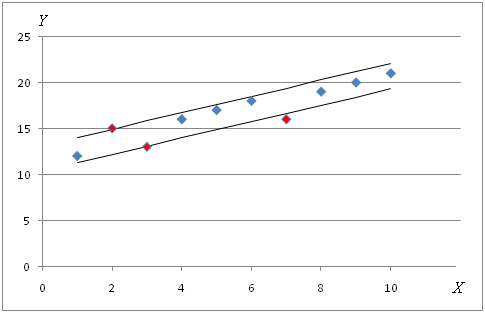
Рис. Найденная линейная зависимость с обозначенным интервалом [–S; +S]