Сумма приращений координат

ОБРАБОТКА РЕЗУЛЬТАТОВ ТЕОДОЛИТНОЙ СЪЕМКИ. ВЫЧИСЛЕНИЕ КООРДИНАТ ВЕРШИН ТЕОДОЛИТНОГО ХОДА. СОСТАВЛЕНИЕ ПЛАНА

8.1. Главные геодезические задачи

8.2. Сумма приращений координат

8.3. Обработка теодолитного хода

8.4. Составление плана

Главные геодезические задачи

Главными геодезическими задачами на плоскости являются прямая и обратная задачи. Прямая геодезическая задача на плоскости формулируется следующим образом: по заданным координатам x₁ и y₁ точки 1, дирекционному углу α и длине d стороны 1-2 вычислить координаты точки 2 (рис. 8.1).

Рис. 8.1. Приращения координат

Вначале вычисляют приращения координат:

;

;

после чего находят координаты определяемой точки

;

.

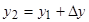Контроль вычислений заключается в вычислении расстояния по формуле

.

Отклонение вычисленного расстояния d от заданного не должно превышать 1 см.

Обратная геодезическая задача на плоскости заключается в вычислении по заданным координатам двух точек (1 и 2) дирекционного угла и длины стороны 1-2.

Для ее решения находят приращения координат

.

После чего, игнорируя знаки приращений координат, вычисляют величину тангенса румба

значение румба

и расстояние

.

Четверть румба определяется в соответствии со знаками приращений координат и (рис. 8.2). Зависимость между дирекционными углами и румбами определяется четвертью румба (рис. 8.3).

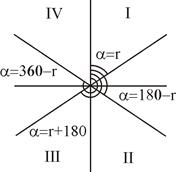
Рис. 8.2. Знаки Dx и Dy Рис. 8.3. Дирекционные углы

Контроль вычислений осуществляется по формулам

.

Расхождения в значениях расстояний не должны превышать 1 – 2 см.

Сумма приращений координат

Для получения теоретической суммы приращений координат разомкнутого теодолитного хода рассмотрим рис. 8.4.

Рис. 8.4. Сумма приращений координат

Из математики известно, что проекция суммы векторов на какую-либо ось равна сумме их проекций. Каждая сторона теодолитного хода может рассматриваться как вектор, представленный направлением и длиной. Поэтому проекция суммы сторон теодолитного хода на какую-либо ось равна сумме их проекций на эту ось. Для каждой стороны теодолитного хода приращения координат Dx и Dy равны проекциям этой стороны на соответствующую ось координат:

;

.

Из чертежа легко видеть, что сумма проекций сторон теодолитного хода на какую-либо ось координат будет равна проекции замыкающей AB на соответствующую ось, а проекция замыкающей равна разности координат исходных пунктов. Следовательно, можно написать равенства

;

.

В замкнутом теодолитном ходе

;

;

поэтому для замкнутого теодолитного хода теоретические суммы приращений координат будут равны

;

.

Вследствие неизбежных ошибок измерений горизонтальных углов и длин сторон теодолитного хода сумма вычисленных приращений координат обычно не равна теоретической сумме приращений. Разности между полученными суммами координат и их теоретическими значениями называют невязками по осям координат:

;

.