Обработка теодолитного хода

Целью обработки теодолитного хода является вычисление координат точек теодолитного хода. Исходными данными для вычисления координат служат результаты полевых измерений (горизонтальные и вертикальные углы и длины сторон теодолитного хода), координаты начального и конечного пунктов теодолитного хода, начальный (и, возможно, конечный) дирекционный угол.

Обработка теодолитного хода выполняется в ведомости вычисления координат (табл. 8.1), где необходимо выполнить следующие действия.

1) Из полевого журнала выписать значения горизонтальных углов и горизонтальных проложений измеренных сторон.

Примечание. Все исходные и измеренные линейные величины выписываются с точностью 0,01 м, угловые – с точностью 0.1¢. Значения тригонометрических функций вычисляются с удержанием 5 цифр после десятичной точки. Все дальнейшие вычисления выполняются с такой же точностью.

2) Из каталога координат пунктов геодезической сети выписать координаты начального и конечного пунктов теодолитного хода, начальный и конечный дирекционные углы. Если в каталоге отсутствуют значения дирекционных углов, то необходимо получить их значения из решения соответствующей обратной геодезической задачи на плоскости.

3) Вычислить сумму измеренных углов .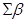

4) Вычислить теоретическую сумму углов хода.

Для разомкнутого хода в случае измеренных правых (по ходу) углов теоретическая сумма углов 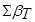равна

,

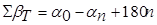где n – число измеренных углов;

если измерены левые углы, то

.

 

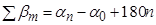Таблица 8.1. Ведомость вычисления координат точек теодолитного хода (углы правые)

 

№ точки	Измерен. угол	Исправл. угол	Дирекц. угол	Длина стороны	Приращения вычисленные	Приращения исправленные	Координаты
DX	DY	DX	DY	X	Y
	°	'	°	'	°	'
A
		-3				18.2
B		17.5		17.2				+2	+3			+6304.73	+2553.28
		-3				01.0	168.47	-76.53	+150.09	-76.51	+150.12
		44.2		43.9				+3	+5			+6228.22	+2703.40
		-2				17.1	211.08	-124.92	+170.15	-124.89	+170.20
		10.0		09.8				+2	+3			+6103.33	+2873,60
		-3				07.3	170.56	-88.16	+146.01	-88.14	+146.04
		03.5		03.2				+3	+4			+6015.19	+3019,64
		-3				04.1	207.11	-109.96	+175.51	-109.93	+175.55
		33.0		32.7				+3	+4			+5905.26	+3195,19
		-2				31.4	187.72	-119.46	+144.80	-119.43	+144.84
		14.2		14.0				+2	+3			+5785,83	+3340,03
		-3				17.4	157.22	-93.05	+126.72	-93.03	+126.75
C		15.8		15.5								+5692,80	+3466,78
						01.9
D
S		18.2		16.3			1102.16	-612.08	+913.28	-611.93	+913.50
SТ		16 3						-611.93	+913.50
fb		+1.9					fx, fy	-0.15	-0.22
f bпред		2.7					fабс	0.27
							fотн	1/4080

Для замкнутого хода теоретическая сумма углов многоугольника вычисляется по формуле

,

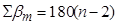где n – число углов в многоугольнике.

5) Вычислить полученную угловую невязку 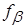как разность измеренной суммы углов и теоретической суммы углов

.

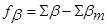6) Найти допустимую угловую невязку по формуле

,

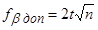где t – точность измерения углов одним приемом; n – число измеренных углов.

7) Проверить выполнение соотношения

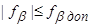
Если соотношение выполняется, то обработка может быть продолжена. Если соотношение не выполняется, то необходимо проверить выписку всех исходных данных (значений измеренных величин из полевых журналов и данных из каталога координат) и проверить все предшествующие вычисления. Если результаты вычислений подтверждаются и полученная угловая невязка больше допустимой, то необходимо выполнить повторные измерения горизонтальных углов теодолитного хода.

8) Вычислить поправки в углы

.

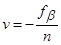Полученные значения поправок округляются до 0.1' и выписываются красным цветом над каждым измеренным значением горизонтального угла как целые числа (см. графу 3 табл.8.1).

 

9) Выполнить контроль вычисления поправок в углы: сумма поправок должна равняться угловой невязке, взятой с обратным знаком

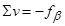
Если данное равенство не выполняется, некоторые поправки могут быть подправлены на 0.1¢ так, чтобы указанное равенство безусловно выполнялось. Желательно, чтобы такие “подправленные” поправки располагались равномерно по ходу.

10) Вычислить значения исправленных углов по формуле

.

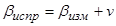11) Выполнить контроль вычисления исправленных углов: сумма исправленных углов должна равняться теоретической сумме углов

.

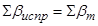Ради выполнения этого соотношения и выполняется введение поправок в измеренные углы.

12) Вычислить дирекционные углы в случае измеренных правых углов по формуле

,

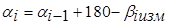а в случае левых углов – по формуле

,

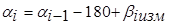13) Проконтролировать вычисление дирекционных углов: значение последнего дирекционного угла должно совпасть с вычисленным значением в случае правых углов

,

 

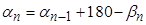а в случае левых углов с

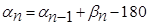
14) Найти приращения координат по формулам:

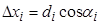
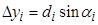
15) Вычислить полученные суммы приращений координат 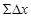и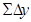

16) Вычислить теоретические суммы приращений координат:

- для разомкнутого хода

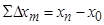
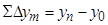
- для замкнутого хода (поскольку и )

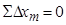
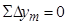
17) Вычислить значения невязок по осям координат

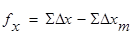
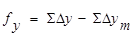
18) Вычислить линейную, или абсолютную, невязку хода

,

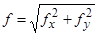19) Вычислить относительную невязку хода

,

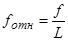где L– длина хода. Относительная невязка представляется в виде дроби с числителем, равным 1, для чего в выражении 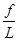числитель и знаменатель необходимо разделить на числитель.

20) Проверить выполнение соотношения

,

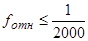где 1/2000 – допустимая относительная ошибка теодолитного хода. Если соотношение не выполняется, то необходимо выполнить проверку всех предыдущих вычислений. Если ошибок не будет обнаружено, то необходимо повторить измерения всех величин (горизонтальных углов и длин сторон). Если соотношение выполняется, то обработка хода может быть продолжена.

21) Вычислить значения коэффициентов:

.

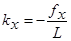
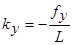Смысл этих коэффициентов – вклад каждого метра хода в значение соответствующей невязки.

22) Найти поправки приращений координат

.

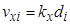
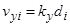Таким образом, поправки в приращения координат принимаются пропорциональными длинам сторон. Значения поправок округляются до 1см и как целые числа записываются красным цветом над значениями соответствующих вычисленных приращений координат.

23) Выполнить контроль вычисления поправок 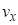и 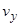: сумма поправок должна равняться соответствующей невязке с противоположным знаком

;

.

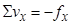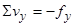Вследствие ошибок округления данные соотношения могут не выполняться. Тогда в некоторые значения поправок (равномерно расположенные по ходу) необходимо прибавить или вычесть по 1 таким образом, чтобы выполнялись указанные соотношения.

24) Вычислить исправленные значения приращений координат

.

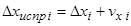
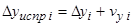25) Выполнить контроль вычисления исправленных приращений координат: сумма исправленных приращений координат должна равняться теоретической сумме приращений координат, то есть должны выполняться соотношения

;

.

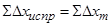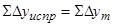26) Вычислить (последовательно) координаты точек теодолитного хода

;

.

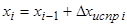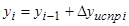27) Проверить вычисление координат: координаты конечной точки хода должны равняться сумме

;

.

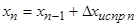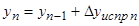При обработке теодолитного хода можно заметить, что вычисления во всех графах ведомости вычисления координат контролируются. Пренебрегать выполнением таких контролей не рекомендуется. Контроль вычислений является обязательным, и переходить к вычислениям в следующей графе можно только после контроля вычислений в текущей графе.

 

8.4. Составление плана

Составление топографического плана по результатам съемки заключается в выполнении следующих действий:

1) построения координатной сетки;

2) накладки точек теодолитного хода;

3) нанесения пикетов;

4) рисовки ситуации;

5) оформления плана.

Топографические планы вычерчиваются в виде отдельных листов размером 50*50 см. Координатная сетка представляет собой сетку квадратов со сторонами 10 см и разбивается с помощью линейки Дробышева (рис. 8.5). Линейка имеет 6 окошек, расстояние между начальными скосами которых составляет 10 см. Расстояние от начального среза первого окна до конца линейки равно длине диагонали квадрата со стороной 50 см, то есть 70.71 см.

 

 

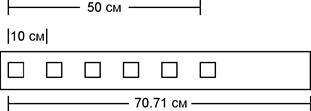
Рис. 8.5. Линейка Дробышева

 

Построение координатной сетки складывается из следующих действий.

1) С помощью линейки Дробышева строят точки A и B с расстоянием между ними 50 см (рис. 8.6).

2) От точек A и B с помощью линейки Дробышева определяют положение точек C и D (линейной засечкой).

3) Проверяют расстояние между точками C и D; его значение не должно отличаться от 50 см более чем на 0.3 мм; после чего размечают все стороны через 10 см.

4) Вычерчивают сетку квадратов и выполняют контроль координатной сетки. Размеры квадратов не должны отличаться от номинальных значений более чем на 0.3 мм.

Если размеры листа плана отличаются от обычных размеров (50 см * 50 см), то сетка координат строится иначе (рис. 8.7).

Проводят диагонали листа и строят точки A, B, C, D, откладывая равные расстояния от точки пересечения диагоналей. Затем на точках A, B, C, D строят четырехугольник и, начиная от какого-либо угла, размечают его стороны через 10 см. Соединяют противоположные метки на сторонах четырехугольника и получают нужную сетку.

 

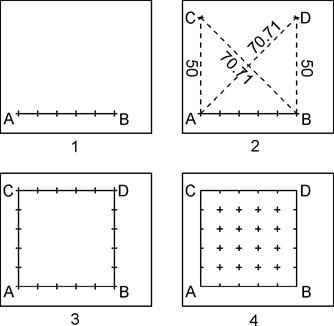
Рис. 8.6. Построение сетки координат

 

После вычерчивания координатной сетки необходимо проверить положение ее вершин. Отклонение фактических размеров квадратов от их номинальных значений не должно превышать 0.3 мм. После этого сетка квадратов подписывается. Если план размещается на нескольких листах, то координаты границ каждого листа выбираются кратными 50M см, где M – знаменатель масштаба вычерчиваемого плана. Например, для масштаба 1:500 границы отдельных листов плана принимаются кратными 250 м, для масштаба 1:1000 – 500 м и т. д. Если план участка местности может быть размещен на одном листе, то координаты границ листа выбирают так, чтобы участок располагался, по возможности, посредине листа.

 

 

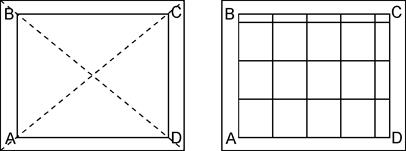
Рис. 8.7. Построение нестандартной сетки

 

Накладка точек теодолитного хода осуществляется по их координатам, выбираемым из ведомости вычисления координат. Контроль нанесения точек теодолитного хода на план выполняется путем измерения на плане расстояний между соседними точками теодолитного хода и сравнением этих расстояний с длинами сторон, указанными в ведомости вычисления координат. Расхождения расстояний на плане не должны превышать 0.3 мм.

Съемочные пикеты на план наносятся в зависимости от способа, использованного при их съемке. Если съемка была выполнена полярным способом, то в качестве полевых материалов служат журнал и абрис. Если съемка была выполнена другими способами, то обычно достаточно абриса, в котором указаны все измеренные величины. Следует отметить, что качество вычерчиваемого плана существенным образом зависит от тщательности, с которой был составлен абрис. Кроме того, как съемка пикетов, так и их нанесение на план осуществляются без контроля, поэтому о правильности и точности составляемого плана можно судить только по взаимному положению пикетов на плане. Однако таким образом можно обнаружить только грубые ошибки, незначительные ошибки во взаимном положении пикетов при этом обнаружить нельзя.

 

Вопросы

 

1. Какие величины являются исходными при обработке теодолитного хода?

2. Чему равна теоретическая сумма углов замкнутого теодолитного хода?

3. Чему равна теоретическая сумма углов разомкнутого теодолитного хода?

4. Как вычисляется угловая невязка теодолитного хода?

5. Как вычисляется допустимая угловая невязка теодолитного хода?

6. Как распределяется угловая невязка в теодолитном ходе?

7. Как контролируется вычисление поправок в углы?

8. Как вычисляются исправленные углы?

9. Как контролируются исправленные углы?

10. Как вычисляются дирекционные углы сторон теодолитного хода?

11. Как контролируются дирекционные углы сторон теодолитного хода?

12. Как вычисляются приращения координат?

13. Как вычисляется теоретическая сумма приращений координат разомкнутого теодолитного хода?

14. Как вычисляется теоретическая сумма приращений координат замкнутого теодолитного хода?

15. Как вычисляется невязка по координатам разомкнутого теодолитного хода?

16. Как вычисляется невязка по координатам замкнутого теодолитного хода?

17. Как вычисляется линейная (абсолютная) невязка теодолитного хода?

18. Что такое относительная ошибка теодолитного хода?

19. Как вычисляется относительная невязка теодолитного хода?

20. Какова допустимая относительная невязка теодолитного хода?

21. Как распределяются невязки по координатам?

22. Как контролируется вычисление поправок в приращения координат?

23. Как вычисляются исправленные значения приращений координат?

24. Как контролируются исправленные значения приращений координат?

25. Как вычисляются координаты?

26. Как контролируется вычисление координат точек теодолитного хода?

27. С какой целью вычисляются координаты точек теодолитного хода?

28. Что требуется для вычисления горизонтальных проложений сторон теодолитного хода?

29. Какие поправки вводятся в измеренные длины сторон теодолитного хода?

30. Что такое главные геодезические задачи на плоскости?

31. В чем заключается прямая геодезическая задача на плоскости?

32. В чем заключается обратная геодезическая задача на плоскости?

33. Перечислите способы теодолитной съемки?

34. В чем заключается теодолитная съемка способом створов?

35. В чем состоит теодолитная съемка способом перпендикуляров?

36. В чем состоит полярный способ теодолитной съемки?

37. В чем состоит съемка способом линейной засечки?

38. Какие имеются ограничения на применение способа линейной засечки?

39. В чем состоит съемка способом угловой засечки?

40. В каких случаях способ угловой засечки является единственно возможным?

41. В каких пределах должен лежать угол линейной или угловой засечки?

42. Что можно сказать о взаимных достоинствах и недостатках различных способов теодолитной съемки?

43. Что такое абрис?

44. Из каких операций складывается составление топографического плана?

45. Каковы стандартные размеры листа топографического плана?

46. Как разбивается координатная сетка на топографических планах?

47. Как контролируется разбивка координатной сетки на топографическом плане?

48. Чему равно допустимое отклонение сторон топографического плана от номинальных размеров?

49. Для чего предназначена линейка Дробышева?

50. Как наносятся точки теодолитного хода на план?

51. Как контролируется нанесение точек теодолитного хода на план?

52. Какова точность нанесения на план точек теодолитного хода?

53. Как строятся на плане точки при съемке способом створов?

54. Как строятся на плане точки при съемке способом перпендикуляров?

55. Как строятся на плане точки при съемке способом линейной засечки?

56. Как строятся на плане точки при съемке способом угловой засечки?

57. Как строятся на плане точки при съемке полярным способом?