 |
Главная |
Синтез ГПТП для комбинационных схем
|
из
5.00
|
Любую комбинационную схему G можно представить в виде множества функционально независимых подсхем Gi, i={1,l} имеющих ri≥1 входов и vi≥1 выходов, где ∑ri=r—количество входов схемы G, а ∑vi=v—количество ее выходов.
Для поверки правильности функционирования схемы G необходимо на каждую подсхему Gi подать всевозможные входные наборы
В случае формирования тестовых последовательностей с помощью генератора М—последовательности для обеспечения всевозможных входных наборов на входах схемы G необходимым является выполнение неравенства:
degφ(x)>r, (2.9)
где degφ(x)=m—старшая степень порождающего полинома φ(x). При этом длина тестовой последовательности 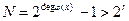 .
.
Цифровые схемы имеют до 480 входов, поэтому их контроль с использованием М—последовательностей, для которых degφ(x)>30-40, является не реальной задачей.
В случае проверки правильности функционирования цифровой схемы не на полном периоде М—последовательности нельзя гарантировать 100%—ную полноту обнаружения всех ее неисправностей. В настоящее время предпринимаются попытки обеспечения 100%—ной полноты покрытия при использовании М—последовательности с длинной периода 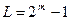 за счет формирования всевозможных входных наборов.
за счет формирования всевозможных входных наборов.
Выражение (2.9) дает верхнюю оценку величины m, определяющей значение старшей степени порождающего полинома φ(х), использование которого на контроле схемы G позволит достичь максимальной полноты контроля. Нижняя оценка для m=degφ(x) будет определяться соотношением
degφ(x)>max ri, однако это выражение только необходимое, но не достаточное условие, которому должен удовлетворять порождающий полином φ(x). Достаточным условием (на его основе формируется тестовая псевдослучайная последовательность) является обеспечение линейной независимости символов, подаваемых одновременно на входы проверяемой комбинационной схемы.
Каждому входу проверяемой комбинационной схемы соответствует определенный разряд входного регистра; таким образом, любой вход i—й комбинационной схемы можно обозначить как 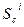 , где с—порядковый номер входа подсхемы Gi, подключенный к
, где с—порядковый номер входа подсхемы Gi, подключенный к 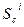 — разряду входного разряда, где формируются псевдослучайные тестовые наборы. Для выполнения необходимого условия значение с={1,ri} должно быть ограничено величиной m. В то же время
— разряду входного разряда, где формируются псевдослучайные тестовые наборы. Для выполнения необходимого условия значение с={1,ri} должно быть ограничено величиной m. В то же время 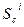 ?{1,2,3,..,p} (p>m —количество разрядов входного регистра).
?{1,2,3,..,p} (p>m —количество разрядов входного регистра).
В зависимости от соотношения величин p и m и от значений 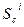 возможны два тривиальных случая выполнения достаточных условий, предъявляемых к порождающему полиному φ(x), когда на выходы каждой подсхемы множества Gi будут поданы всевозможные двоичные наборы. Достаточные условия будут выполняться при:
возможны два тривиальных случая выполнения достаточных условий, предъявляемых к порождающему полиному φ(x), когда на выходы каждой подсхемы множества Gi будут поданы всевозможные двоичные наборы. Достаточные условия будут выполняться при:
p=m и, во—вторых, при p>m и
max(max 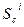 -min
-min 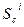 )<m. Для случая i?{1,l},
)<m. Для случая i?{1,l},
max 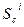 -min
-min 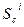 ≥m необходимо обеспечение линейной
≥m необходимо обеспечение линейной
независимости символов входных наборов. Это достигается выбором соответствующего порождающего полинома φ(x) из множества полиномов, для которых degφ(x)=m.
|
из
5.00
|
Обсуждение в статье: Синтез ГПТП для комбинационных схем |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

