Обработка результатов экспертного опроса, проведенного по методу нормирования

Результаты опроса, проведенного по методу нормирования, пред­ставляются в виде матрицы ||W_jⁱ|| ( –индекс столбцов, – индекс строк).

Анализ оценок каждого эксперта. Оценки объектов, полученные по методу нормирования, проверить не представляется возможным. Но мож­но по оценкам эксперта определить его компетентность. В п. 2 указывалось, что одним из подходов к оценке компетентности является подход, основан­ный на учете оценок эксперта в экспертизе.

Суть этого подхода в том, что компетентным считают эксперта, оценки которого близки к групповым.

Критерием соответствия оценок эксперта с групповыми оценками является коэффициент корреляции:

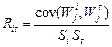. (105)

Но R_iг может принимать отрицательное значение, что затрудняет интерпре­тацию его в качестве коэффициента компетентности. Поэтому для харак­теристики компетентности экспертов как степени близости их оценок к групповым используется выражение (106), которое больше нуля при по­ложительных :

. (106)

Отметим, что коэффициент компетентности, вычисляемый по формуле (106), линейно связан с коэффициентом корреляции (105).

Групповые оценки объектов в методах, основанных на шкалах отношений или интервалов, вычисляются как среднее личных оценок эк­спертов, причем, если известны характеристики компетентности экспер­тов, то их личные оценки взвешиваются:

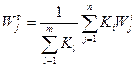. (107)

Выражение (107), как и среднее, является адекватной статистикой для шкал отношений и интервалов [1].

Для определения K_i используем итерационную процедуру, на каж­дом шаге t которой будем вычислять 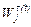по формуле (107), а затем К_i^(t) путем подстановки 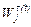в (106).

Представив коэффициенты компетентности и виде вектора-столбца , а групповые оценки объектов и виде вектора-столбца , формулы (106) и (107) итерационной процедуры запишем в виде:

, (108)

, (109)

где транспонированная матрица .

Обозначив 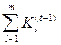через l^(t-1) и подставив (108) в (109), получим:

. (110)

Матрицу размерности , полученную произведением матриц ||W ⁱ_j||^T и ||W ⁱ_j ||, обозначим через || b_il ||, тогда (110) перепишется в виде:

. (111)

Отметим, что все элементы матрицы |[ b_il || положительны и вы­числяются по формуле: .

Векторное выражение (111) точно такое же, как и (87) для опре­деления групповых оценок в методе попарного сравнения. Как указыва­лось в п. 6, при большом числе итераций эта процедура сходится, а резуль­татом будет собственный вектор матрицы ||b_il||, соответствующий максимальному действительному собственному числу.

Таким образом, коэффициенты компетентности экспертов опре­деляются как собственный вектор матрицы ||b_il||, полученной попар­ным скалярным произведением столбцов матрицы оценок объектов ||W ⁱ_j||.

Определение групповых оценок объектов. В методах, основанных на шкалах отношений и интервалов, определяются точечные и интервальные оценки объектов. Так как каждый эксперт может иметь свой коэффициент компетентности, который является характеристикой точности его оценок, то для определения групповых оценок используется аппарат обработки не­равноточных наблюдений [8].

Точечная оценка групповой оценки объекта j вычисляется как средневзвешенная личных оценок:

. (112)

Точечная групповая оценка без указания точности и надежности малоопределенна, так как 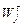следует рассматривать как случайную ве­личину, зависящую от состава экспертов. Если представить гипотетическую ситуацию, когда опросили всех возможных экспертов (генеральную сово­купность экспертов), то получим истинную оценку объекта W_j^*. Вычисленная же по формуле (112) 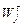, является оценкой W_j^*.

Для того чтобы получить представление о точности и надежности оценки 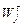для W_j^* определим интервал ( 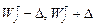), который будет включать W_j^* с заданной вероятностью P_д. Такой интервал назы­вается доверительным интервалом, а P_д – доверительной вероятностью.

Для определения доверительного интервала W_j^* воспользуемся ме­тодикой расчета доверительного интервала среднего при неравноточных наблюдениях [8].

Сначала вычисляется оценка дисперсии 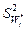в соответствии с выражением:

,

где 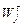определяется по формуле (112).

Случайная величина 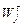распределена по закону Стьюдента с математическим ожиданием W_j*, дисперсией 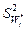и числом степеней свободы .

Задавшись доверительной вероятностью P_д (обычно P_д > 0,70), находим квантиль распределения Стьюдента (в приложении 9 приве­дены квантили t для и ), соответствующий . Тогда в интервал [a,b] (рис. 6) с вероятностью P_д будут попадать все W_j. Если же построить симметричный относительно вычисленного по формуле (112) 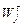такой же интервал (на рис. 6 он выделен), то можно утверждать, что с вероятностью P_д он будет включать W_j^*. Значит границы довери­тельного интервала будут определяться следующим выражением:

.

Если доверительный интервал включает отрицательные значения (нижняя граница меньше нуля), то надежность групповой оценки этого объекта низка и системный аналитик должен сделать необходимые выво­ды: или исключить из рассмотрения этот объект, или уточнить у экспертов оценки объекта.

В заключение остановимся на вопросе приведения личных шкал из­мерения экспертов к единой шкале, так как групповые оценки объектов можно получить, используя оценки экспертов измеренные в одной шкале.

В п. 1 указывалось, что в большинстве случаев приведение личных шкал к единой осуществляется путем нормировки оценок каждого эк­сперта:

. (113)

Это объясняется тем, что единая шкала измерения (шкала отношении) задается одним шкальным значением, равным 1, соответствующим гипо­тетическому объекту (О_э), у которого проявление измеряемого свойства равно суммарному проявлению свойства всех объектов:

.

Используя тот же самый подход приведения личных шкал к единой, можно задать единую шкалу, указав шкальное значение одного из объектов, на­пример,m(О₁) = 1. Тогда личные оценки эксперта i будут приводиться к единой шкале по формуле:

. (114)

Выбор единой шкалы не должен, в конечном итоге, отражаться на груп­повых оценках. Однако если использовать для нормировки оценок (113) или (114), то групповые оценки могут отличаться даже порядком. Напри­мер, пусть даны оценки двух равнокомпетентных экспертов:

	Э1	Э2
О1	0,5	0,5
О2	0,3	0,5
О3	0,2	1,0

Если для приведения к единой шкале воспользоваться нормиров­кой (113), а затем определить групповые оценки объектов по формуле (112), то получим = 0,375; = 0,275; = 0,350. При использова­нии формулы (114) для нормирования личных оценок получим: = 1,0; = 0,80; = 1,2. При использовании различных единых шкал групповыеоценки объекта 1 и 3 отличаются порядком.

Это объясняется тем, что личные шкалы экспертов не эквивалентны (в приведенном примере порядок объектов у экспертов различен), а, значит, и шкалы, в которых измеряются групповые оценки, не эквивалентны.

Следовательно, выбор формулы (113) для нормирования оценок эк­спертов должен быть специально обоснован, в противном случае, ее исполь­зовать нельзя. Чтобы исключить проблему приведения личных шкал к еди­ной, необходимо при опросе экспертов задать один объект-эталон, относи­тельно которого осуществлять оценки других объектов (если осуществляется измерение по шкале отношений) или два эталона (если свойство измеряется по шкале интервалов).

На практике формулу (113) для нормирования используют в тех слу­чаях, когда коэффициент согласия экспертов достаточно большой. В этом случае с некоторым приближением можно считать, что личные шкалы эк­спертов эквивалентны.

Анализ достоверности групповых оценок. Как указывалось выше, одной из оценок достоверности (надежности) групповых оценок являются доверительные интервалы. Помимо этого, достоверность может быть оце­нена через коэффициент согласия экспертов и устойчивость групповых оце­нок.

Оценка согласованности экспертов. Коэффициент согласия вычис­ляется в соответствии с общей формулой (1), которую запишем в виде:

 

(115)

Получим статистику для проверки значимости коэффициента со­гласия. Из выражения (115) следует, что 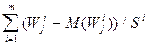при достаточно большом числе экспертов (m >5) стремится к нормальному закону с математическим ожиданием, равным нулю, и дисперсией m. Тогда распределено но закону c² (Пирсона) с числом степеней свободы n = n - 1. [3]. Следовательно, статистикой для проверки значимости E будет:

.

Решающим правилом для того, чтобы считать коэффициент согласия зна­чимым и, соответственно, групповые оценки достоверными, является не­равенство:

.

 

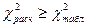ПРИЛОЖЕНИЕ 1

Функция вероятности S^'(d²) [6]

Знаки целой части у P опущены; например, для и значение P равно 0,042

n=4	n=5	n=6	n=7	n=8
S	P	S	P	S	P	S	P	S	P

Продолжение

n=9	n=10	n=11	n=12	n=13
S	Р	S	Р	S	Р	S	P	S	Р

Примечание. Поскольку распределение является симметричным,

.

ПРИЛОЖЕНИЕ 2

Распределение S [6]

Вероятность того, что данное значение S будет достигнуто или прев­зойдено, для 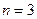и m от 2 до 10 (знаки целой части вероятностей опу­щены)

 

S	m=2	m=3	m=4	m=5	m =6	m=7	m=8	m=9	m =10

 

n=4	n=5
S	m=3	m=5	S	m=2	m=4	m =6	S	m=3