 |
Главная |
АНАЛИЗ ПОЛИТРОПНЫХ ПРОЦЕССОВ
|
из
5.00
|
Проведем анализ политропных процессов расширения, представив их в pv-диаграмме (рис. 1.11).
|
|

Политропные процессы расширения делятся на три группы, которые отличаются распределением q, Δu и l (табл. 1.2).
Первая группа включает процессы (см. рис. 1.11), расположенные между изохорой с подводом теплоты (п = - ∞) и изотермой (и = 1), т.е. все процессы расширения с показателем политропы - ∞ < п< 1. Теплота подводится + q:
одна часть ее работы расходуется на работу расширения /, а другая - на изменение внутренней энергии газа Δu. По мере удаления от изохоры (п = - ∞) и приближения к изотерме (п = 1), т.е. с увеличением показателя п доля подводимой теплоты, затрачиваемая на работу, возрастает.
Теплоемкость процессов этой группы положительная.
Вторая группа политропных термодинамических процессов расположена между изотермой расширения (п = 1) и адиабатой (п = k), т.е. в эту группу входят процессы с показателем политропы 1 < п < k. Теплота подводится, но работа расширения совершается также частично за счет внутренней энергии газа (Δu). В процессах этой группы температура газа уменьшается. При приближении к адиабате (п = k) все большая часть работы расширения совершается за счет уменьшения внутренней энергии. Теплоемкость процессов этой группы отрицательна.
Третья группа процессов расположена в области между адиабатой расширения (п = k) и изохорой с отводом теплоты (п = + ∞). Следовательно, в эту группу входят политропные процессы с показателем k < п < + ∞. Теплота не подводится. Работа расширения газа совершается за счет внутренней энергии, но, кроме того, часть внутренней энергии отводится в виде теплоты. Теплоемкость политропных процессов этой группы положительна.
Пример 1. В закрытом сосуде вместимостью 4 м3 находится воздух при
p 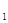 = 0,1 МПа и t
= 0,1 МПа и t 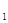 = 27 °C. В результате подвода теплоты температура газа повысилась до t
= 27 °C. В результате подвода теплоты температура газа повысилась до t  = 500 °C. Требуется определить конечное давление p
= 500 °C. Требуется определить конечное давление p  количество подведенной теплоты Q и изменение энтальпии ΔH. Теплоемкость воздуха считают нелинейной, зависящей от температуры.
количество подведенной теплоты Q и изменение энтальпии ΔH. Теплоемкость воздуха считают нелинейной, зависящей от температуры.
Решение. Из уравнения состояния находим

Конечное давление
Р  =Р
=Р 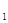 ·T
·T  /T
/T 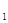 = 0,1·773/300 =0,258 МПа. (T ≈ t + 273 К).
= 0,1·773/300 =0,258 МПа. (T ≈ t + 273 К).
Средняя теплоемкость воздуха

Средняя изобарная теплоемкость

Количество подведенной теплоты

Изменение энтальпии

Пример 2. Кислород в количестве 1 кг адиабатно расширяется от начального состояния, определяемого давлением p 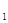 = 1,0 МПа и температурой t
= 1,0 МПа и температурой t 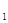 = 277 °С, до конечного состояния с давлением p
= 277 °С, до конечного состояния с давлением p  = 0,1 МПа. Требуется определить конечные параметры газа V
= 0,1 МПа. Требуется определить конечные параметры газа V  ,T
,T  и работу расширения l.
и работу расширения l.
Решение. Из уравнения Клапейрона находим удельный объем

Конечный объем v  находим из соотношения параметров в адиабатном процессе (для двухатомных газов k = С
находим из соотношения параметров в адиабатном процессе (для двухатомных газов k = С 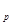 /
/  = 1,4):
= 1,4):
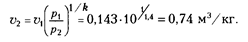
Работа, совершаемая газом в адиабатном процессе, определяется по уравнению

Конечная температура газа
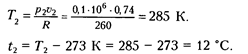
|
из
5.00
|
Обсуждение в статье: АНАЛИЗ ПОЛИТРОПНЫХ ПРОЦЕССОВ |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы



