Теорема умножения вероятностей

Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие имело место:

(доказательство самостоятельно)

Следствия: 1. Вероятность произведения двух независимых событий равна произведению вероятностей этих событий: .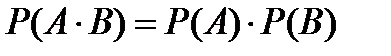

2. Обобщим теорему на случай конечного числа событий.

Вероятность произведения конечного числа событий равна произведению вероятностей этих событий, причём вероятность каждого следующего по порядку события вычисляется при условии, что все предыдущие имели место:

Пример: В урне 2 белых и 3 чёрных шара. Из урны вынимают подряд 2 шара. Найти вероятность того, что оба шара белые.

Решение: А₁ - появление белого шара при первом вынимании,

А₂ - появление белого шара при втором вынимании,

А - появление двух белых шаров.

а) шар не возвращается в урну: ;

б) шар возвращается в урну: .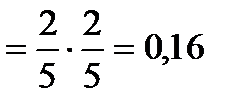

§5. Формула полной вероятности. Формула Байеса.

Следствием двух основных теорем теории вероятностей – теоремы сложения и теоремы умножения – являются формулы полной вероятности и Байеса (Байес Томас английский математик 1702-1761).

Пусть событие А может произойти только при условии появления одного из событий Н₁, Н₂,…, Н_n, образующих полную группу несовместных событий. Будем эти события Н_i называть гипотезами.

В этом случае имеет место формула полной вероятности:

Доказательство.

Так как, Н₁, Н₂,…, Н_n образуют полную группу, то

Применим теоремы сложения и умножения вероятностей (учитывая, что – несовместные события):

Или , что и требовалось доказать.

Пусть событие А произошло. Необходимо выяснить, изменятся ли вероятности гипотез. Р(Н₁), Р(Н₂), …, Р(Н_n) – априорные вероятности;

Р(Н_i/A) – апостериорные вероятности (получаемые после проведения испытания).

По теореме умножения вероятностей 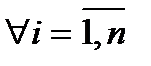имеем:

тогда

Воспользуемся формулой полной вероятности и получим формулы Байесаили теорему гипотез:

Значение формулы Байеса состоит в том, что при наступлении события А, то есть по мере получения новой информации, мы можем проверять и корректировать выдвинутые до испытания гипотезы Н_i. Такой подход, называемый байесовским, даёт возможность корректировать управленческие решения в экономике, оценки неизвестных параметров распределения изучаемых признаков в статистическом анализе и т.п.

Пример: В торговую фирму поступили телевизоры от трёх поставщиков в отношении 1:4:5. Практика показала, что телевизоры, поступающие от 1-го,

2-го и 3-го поставщиков, не потребуют ремонта в течение гарантийного срока соответственно в 98, 88 и 92% случаев.

1) Найти вероятность того, что поступивший в торговую фирму телевизор не потребует ремонта в течение гарантийного срока.

2) Проданный телевизор потребовал ремонта в течение гарантийного срока. От какого поставщика вероятнее всего поступил этот телевизор?

Решение:

1)Пусть Н_i - телевизор поступил в торговую фирму от i -го поставщика.

По условию: ; ; .

А – телевизор не потребует ремонта в течение гарантийного срока.

Р(А/H₁)=0,98; Р(А/H₂)=0,88; Р(А/H₃)=0,92

Тогда

2) – телевизор потребует ремонта в течение гарантийного срока

; ; ;

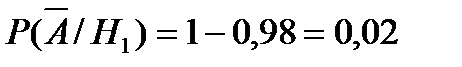Наиболее вероятна гипотеза Н₂ - поступление данного телевизора от 2-го поставщика.