РАСЧЕТ ЧЕРВЯЧНОЙ ПЕРЕДАЧИ

2.1. Исходные данные.

- передаточное число: u_p = 22

- число заходов червяка: z₁ = 2

- передача не реверсивная со слабыми толчками;

- расположение червяка – боковое;

- эквивалентное число циклов нагружения на валу червячного колеса

N_HElll = 44253363;

Остальные данные приведены в таблице 2.1:

Таблица 2.1. Основные энергокинематические параметры передачи

№ вала	, об/мин	, рад/с	,кВт	,
I (червяк)		150,80	6,246	41,4
II (червячное колесо)	65,45	6,85	4,680	683,2

 

 

2.2. Число зубьев червячного колеса:

z₂= u_p·z₁ = 22·2 = 44

Принимаем : z₂= 44

2.3.Коэффициент диаметра червяка:

q = z₂ /4 = 44/4 = 11; принимаем q=11

2.4.Определяем ориентировочное значение линейной скорости скольжения в контакте нарезки червяка и зубьев червячного колеса:

n₃- частота вращения червячного колеса, об/мин

T_lll – вращающий момент на валу червячного колеса , об/мин

2.5.Выбор материалов червяка и червячного колеса (таблица 2)

Таблица 2. Материалы, применяемые для червячной передачи

 

Червячное колесо	Червяк
Материал		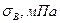	Материал	Твердость
БРоФ 10-1			Сталь 40ХН	HRC 50…60

 

Предварительно принимаем конструкцию червячного колеса с венцом из бронзы и колесным центром из чугуна.Червяк из стали.

Предел контактной выносливости материала венца колеса при нормативном количестве циклов нагружения определяем по формуле:

= 0,8 · σ_в = 0,8·240= 192 МПа.

Коэффициент долговечности:

0.83

Допускаемое контактное напряжение для материала венца колеса:

= 192·0,83 = 159 МПа.

2.6.Допускаемое напряжение изгиба зубьев колеса с бронзовым венцом определяем по формуле, соответствующей нереверсивному режиму работы передачи:

= (0,08· σ_в+ 0,25·σ_Т ) · К_FL = (0,08·240+0,25·160) ·0,66 = 39,1 Мпа

Коэффициент долговечности:

2.7.Расчет межосевого расстояния:

Расчетное значение межосевого расстояния определяем по формуле:

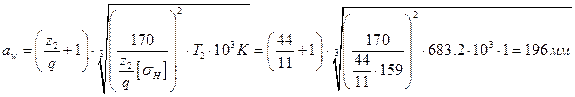
где - коэффициент нагрузки для червячных передач;

- коэффициент, зависящий от характера изменения нагрузки и от деформации червяка = 1 ;

- коэффициент, зависящий от точности изготовления передачи и скорости скольжения =1;

- принимаем степень точности червячной передачи - 7-ю.

Скорректируем значение межосевого расстояния по стандартному ряду.

В нашем случае стандартное значение α_w = 196 мм.

2.8.Осевой модуль зацепления:

Расчетное значение:

2·180 / 11+44 = 6,54 мм.

Действующее контактное напряжение в сопряжении передачи:

=

Проводим проверку выполнения условия прочности по контактным напряжениям. Для этого сравним действующее контактное напряжение с допускаемым .

Условие контактной прочности соблюдено. Недогруз составляет:

2.10.Определение коэффициента формы зуба:

Коэффициент формы зуба червячного колеса: 1,50 , при z₂=44

2.11.Определение действующего напряжения изгиба:

Напряжение изгиба, действующее на зуб червячного колеса, находящегося в зацеплении:

 

где - угол подъема на делительном цилиндре червяка в градусах и минутах: = ;

- преобразуем минуты в градусы: = 9⁰ + (27^′ / 60⁰) = ;

- преобразуем градусы в радианы: = ;

- коэффициент упрочнения зуба: =

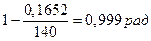
После подстановки числовых значений получим:

9,6 МПа.

2.12.Проверка передачи на выносливость при циклическом изгибе зубьев колеса.

Условие обеспечения прочности при таком виде нагружения имеет вид:

.

В нашем случае условие изгибной прочности соблюдается .

Вывод: пересчет параметров не требуется.

2.13.Определение геометрических параметров червячной пары.

Диаметры делительных окружностей:

- червяка: 7·12 = 84 мм;

- червячного колеса: 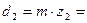7·44 = 308 мм.

Диаметры окружностей выступов:

- червяка: 84+2·7 = 98 мм;

- червячного колеса: 308+2·7 = 322 мм.

Диаметры окружностей впадин:

- червяка: 84-2,4·7 = 67,2 мм;

- червячного колеса: 308-2,4·7 = 291,2 мм.

Ширина червячного колеса:

0,67·98 = 72 мм

20.5 Длина нарезанной части червяка: при z₁ = 2

2.14.Усилия, действующие в зацеплении.

Окружная сила червяка (осевая сила колеса ):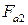

Н.

Окружная сила колеса (осевая сила червяка ):

Радиальная сила в зацеплении:

4436·tg20⁰ = 1625 Н.

Расстояние между опорами червяка;

= 322+20 = 332 мм.

Минимальный момент инерции поперечного сечения червяка.

= 3,14·67,2⁴ / 64 = 1001030 мм⁴.

2.15.Проверка червяка на жесткость.

Прогиб червяка определяется по формуле:

Е = МПа – модуль упругости материала червяка;

I – минимальный момент инерции поперечного сечения червяка.

В рассматриваемом случае условие жесткости

соблюдается .