Что такое канонический вид уравнения?

Это общепринятый стандартный вид уравнения, когда в считанные секунды становится ясно, какой геометрический объект оно определяет. Кроме того, канонический вид очень удобен для решения многих практических заданий. Так, например, по каноническому уравнению 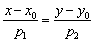«плоской» прямой, во-первых, сразу понятно, что это прямая, а во-вторых – элементарно просматривается принадлежащая ей точка и направляющий вектор .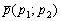

Очевидно, что любая линия 1-го порядка представляет собой прямую. На втором же этаже нас ждёт уже не вахтёр, а гораздо более разнообразная компания из девяти статуй:

Классификация линий второго порядка

С помощью специального комплекса действий любое уравнение линии второго порядка приводится к одному из следующих видов:

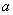( и 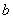– положительные действительные числа)

1) 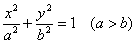– каноническое уравнение эллипса;

2) 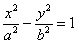– каноническое уравнение гиперболы;

3) 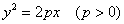– каноническое уравнение параболы;

4) 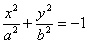– мнимый эллипс;

5) 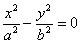– пара пересекающихся прямых;

6) 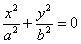– пара мнимых пересекающихся прямых (с единственной действительной точкой пересечения в начале координат);

7) 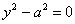– пара параллельных прямых;

8) 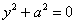– пара мнимых параллельных прямых;

9) 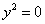– пара совпавших прямых.

У ряда читателей может сложиться впечатление неполноты списка. Например, в пункте №7 уравнение 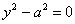задаёт пару прямых 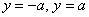, параллельных оси 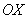, и возникает вопрос: а где же уравнение 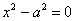, определяющее прямые 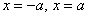, параллельные оси ординат? Ответ: оно не считается каноническим. Прямые 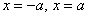представляют собой тот же самый стандартный случай 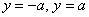, повёрнутый на 90 градусов, и дополнительная запись 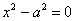в классификации избыточна, поскольку не несёт ничего принципиально нового.

Таким образом, существует девять и только девять различных видов линий 2-го порядка, но на практике наиболее часто встречаются эллипс, гипербола и парабола.

Сначала рассмотрим эллипс. Как обычно, я акцентирую внимание на тех моментах, которые имеют большое значение для решения задач, и если вам необходим подробный вывод формул, доказательства теорем, пожалуйста, обратитесь, например, к учебнику Базылева/Атанасяна либо Александрова..

Эллипс и его каноническое уравнение

Правописание… пожалуйста, не повторяйте ошибок некоторых пользователей Яндекса, которых интересует «как построить эллибз», «отличие элипса от овала» и «эксцентриситет элебса».

Каноническое уравнение эллипса имеет вид , где 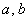– положительные действительные числа, причём . Само определение эллипса я сформулирую позже, а пока самое время отдохнуть от говорильни и решить распространённую задачу:

Как построить эллипс?

Да, вот взять его и просто начертить. Задание встречается часто, и значительная часть студентов не совсем грамотно справляются с чертежом:

Пример 1

Построить эллипс, заданный уравнением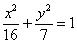

Решение: сначала приведём уравнение к каноническому виду:

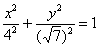
Зачем приводить? Одно из преимуществ канонического уравнения заключается в том, что оно позволяет моментально определить вершины эллипса, которые находятся в точках 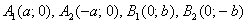. Легко заметить, что координаты каждой из этих точек удовлетворяют уравнению .

В данном случае :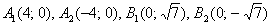

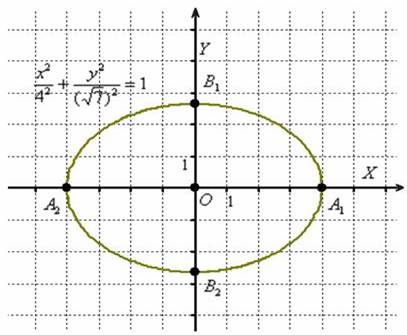
Отрезок 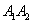называют большой осью эллипса;
отрезок 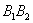– малой осью;
число 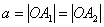называют большой полуосью эллипса;
число 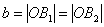– малой полуосью.
в нашем примере: .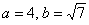

Чтобы быстро представить, как выглядит тот или иной эллипс достаточно посмотреть на значения «а» и «бэ» его канонического уравнения.

Всё ладно, складно и красиво, но есть один нюанс: я выполнил чертёж с помощью программы. И вы можете выполнить чертёж с помощью какого-либо приложения. Однако в суровой действительности на столе лежит клетчатый листок бумаги, и на наших руках водят хороводы мыши. Люди с художественным талантом, конечно, могут поспорить, но мыши есть и у вас тоже (правда, поменьше). Таки не зря человечество изобрело линейку, циркуль, транспортир и другие нехитрые приспособления для черчения.

По этой причине нам вряд ли удастся аккуратно начертить эллипс, зная одни вершины. Ещё куда ни шло, если эллипс небольшой, например, с полуосями 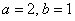. Как вариант, можно уменьшить масштаб и, соответственно, размеры чертежа. Но в общем случае крайне желательно найти дополнительные точки.

Существует два подхода к построению эллипса – геометрический и алгебраический. Построение с помощью циркуля и линейки мне не нравится по причине не самого короткого алгоритма и существенной загроможденности чертежа. В случае крайней необходимости, пожалуйста, обратитесь к учебнику, а в реальности же гораздо рациональнее воспользоваться средствами алгебры. Из уравнения эллипса 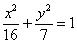на черновике быстренько выражаем:

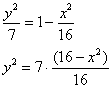
Далее уравнение распадается на две функции:
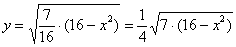– определяет верхнюю дугу эллипса;
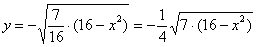– определяет нижнюю дугу эллипса.

Любой эллипс симметричен относительно координатных осей, а также относительно начала координат. И это отлично – симметрия почти всегда предвестник халявы. Очевидно, что достаточно разобраться с 1-ой координатной четвертью, поэтому нам потребуется функция 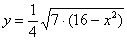. Напрашивается нахождение дополнительных точек с абсциссами 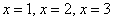. Настукаем три смс-ки на калькуляторе:

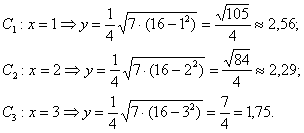
Безусловно, приятно и то, что если допущена серьёзная ошибка в вычислениях, то это сразу выяснится в ходе построения.

Отметим на чертеже точки 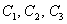(красный цвет), симметричные точки на остальных дугах (синий цвет) и аккуратно соединим линией всю компанию:

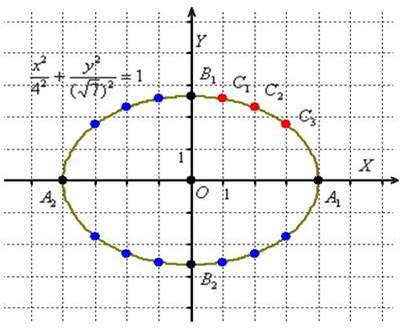
Первоначальный набросок лучше прочертить тонко-тонко, и только потом придать нажим карандашу. В результате должен получиться вполне достойный эллипс. Кстати, не желаете ли узнать, что это за кривая?