Расчет зубьев цилиндрической прямозубой передачи на контактную прочность

Контактная прочность зубьев является основным критерием работоспособности закрытых, обильно смазываемых и защищенных от абразива зубчатых передач. Расчет на контактную прочность включает расчеты на выносливость и на предотвращение разрушения рабочих поверхностей зубьев при максимальной нагрузке (§ 11.7).

Расчет на выносливость. Разрушение начинается вблизи полюса. Поэтому расчетные напряжения определяют на линии контакта, проходящей через полюс 77 (рис. 11.19, а).

Цель расчета — определение размеров передачи и материала колес, при которых не будет прогрессивного выкрашивания. Критерий прочности запишется так: σ// ^Мя, где с ff — расчетное напряжение, зависящее от геометрических параметров передачи, величины и характера нагрузки; [σ]^ — допускаемое напряжение, зависящее от состояния материала колес.

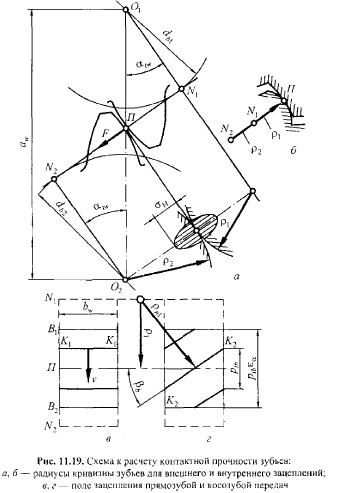
В качестве исходной принимают формулу Герца для максимальных контактных напряжений ои в центре площадки контакта двух цилиндров при их сжатии где F— нормальная к поверхности результирующая сила сжатия: £|, Е2 — модули упругости; V| , v2 — коэффициенты Пуассона материалов колес; 1Х — суммарная длина контактных линий; ρ — приведенный радиус кривизны

Для получения расчетной зависимости заменим величины, входящие в формулу Герца, параметрами зацепления

Суммарная длина контактных линий К\К\ в плоскости зацепления Ζ?|Ζ?2 (рис. 11.19, в) в прямозубой передаче колеблется. В зоне однопарного зацепления суммарная длина контактных линий равна bn. (в полюсе IT), в зоне двухпарпого зацепления — 2bw . Для расчетов принимают

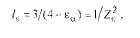где са — коэффициент торцового перекрытия, Zr — коэффициент, учитывающий суммарную длину контактных линий. Из предыдущей зависимости

При εα =1,2...1,8 значение Zr =0,966...0,856. В среднем можно принять ZE « 0,9 .

 

41. Силы в зацеплении

 

Силы принято определять в полюсе W (рис.5) зацепления.

 

Рис.5

 

По линии зацепления b – b (рис. 5) действует нормальная сила Fn. Для удобства расчетов силу Fn принято раскладывать на три составляющие:

1) Ft – окружная сила, направленная по касательной к делительным окружностям. Это основная, движущая, полезная сила. На колесе z2 Ft совпадает с направлением вращения n2. На шестерне z1 F направлена против вращения n1.

Следовательно, на рис. 5 дана схема сил для шестерни:

 

Ft = 2000Т / d, (1)

 

где Т – Н∙м; d – мм;

2) Fr – радиальная сила, направленная по линии центров (радиусам). Для внешнего зацепления – к оси вращения, для внутреннего – от оси.

В торцовой плоскости t – t (рис. 5) имеем

 

Fr = tgбt, (2)

 

где бt – делительный угол профиля в торцовой плоскости: tgбt = tgбn / cosв; бn– нормальный угол зацепления, в – угол наклона зубьев. В практических расче-тах бt ≈ бn =20°.

3) Fa – осевая сила, направленная параллельно оси а – а зубчатого коле-

са. Силы Ft и Fа как составляющие нормальной силы Fn′, всегда находятся вне линии зуба (рис. 5). В делительной плоскости:

 

Fа = Fttgв. (3)

 

Необходимый в дальнейших расчетах основной угол наклона зуба

вb (в основной плоскости зацепления b) определяется как вb = arcsin(sinвcosбn).

Полная нормальная сила (рис. 5):

 

Fn = Fnt / cosвb = Ft / (cosбtcosвb). (4)

 

Для прямозубых передач во всех формулах в = вb = 0; бt = бn = б;

 

Ft = 2000T / d; Fr = Fttgб; Fa = 0; Fn = Ft / cosб.

 

Недостатком косозубых передач является наличие осевых сил Fа, которые дополнительно нагружают опоры валов, усложняя их конструкцию.

 

в

n

Fa /2

Ft /2

в

Fa /2

Рис. 6

В косозубых передачах углы в ограничены в пределах 8…18°.

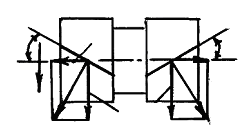
Указанный недостаток устранен в шевронной передаче, которая представляет собой сдвоенную косозубую с противоположным наклоном зубьев на полушевронах. Из рис. 6 видно, что осевые силы Fа /2 взаимоуравновешены.

 

 

42. Геометрические параметры. У косозубых колес зубья располагаются не по образующей делительного цилиндра, а составляют с ней некоторый угол β (рис. 8.23, где а — косозубая передача; б— шевронная, и рис. 8.24).

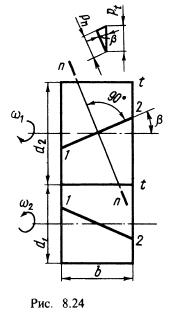
Оси колес при этом остаются параллельными. Для нарезания косых зубьев используют инструмент такого же исходного контура, как и для нарезания прямых. Поэтому профиль косого зуба в нормальном сечении η — η совпадает с профилем прямого зуба. Модуль в этом сечении должен быть также стандартным.

В торцовом сечении t — t параметры косого зуба изменяются в зависимости от угла β: окружной шаг pt=pn/cos β, окружной модуль mt = mn/cos β, делительный диаметр d=mtz = mnz/cos β. Индексы η и t приписывают параметрам в нормальном и торцовом сечениях соответственно.

Прочность зуба определяют его размеры и форма в нормальном сечении. Форму косого зуба в нормальном сечении принято определять через параметры эквивалентного прямозубого колеса (рис. 8.25).

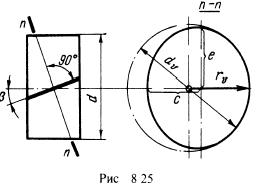
Нормальное к зубу сечение образует эллипс с полуосями с —г и e — r\cos β, где r = d/2. В зацеплении участвуют зубья, расположенные на малой оси эллипса, так как второе колесо находится на расстоянии c = d/2. Радиус кривизны эллипса на малой оси (см. геометрию эллипса)

rv = e2/с = г/cos2 β.

 

 

43. Конические зубчатые колеса применяют в передачах, у которых оси валов пересекаются под некоторым углом £ (рис. 8.29 и 8.30). Наиболее распространены передачи с углом £ = 90°.

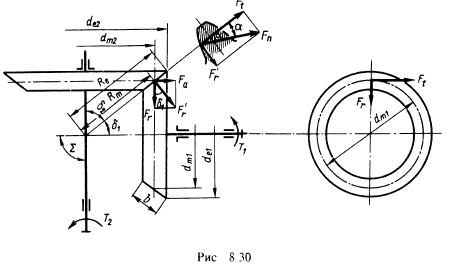
Конические передачи сложнее цилиндрических в изготовлении и монтаже. Для нарезания конических колес требуются специальные станки и специальный инструмент. Кроме допусков на размеры зубьев здесь необходимо выдерживать допуски на углы δ! и δ2, а при монтаже обеспечивать совпадение вершин конусов. Выполнить коническое зацепление с той же степенью точности, Рис. 8.29 что и цилиндрическое, значительно труднее.

Пересечение осей валов затрудняет размещение опор. Одно из конических колес, как правило, располагают кон- сольно. При этом увеличивается неравномерность распределения нагрузки по длине зуба (см. рис. 8.13). В коническом зацеплении действуют осевые силы, наличие которых усложняет конструкцию опор. Все это приводит к тому, что, по опытны данным, нагрузочная способность конической прямозубой передачи составляет лишь около 0,85 цилиндрической. Несмотря на отмеченные недостатки, конические передачи имеют широкое применение, поскольку по условиям компоновки механизмов иногда необходимо располагать валы под углом.

Геометрические параметры. Аналогами начальных и делительных цилиндров цилиндрических передач в конических передачах являются начальные и делительные конусы с углами 5t и δ2. При коэффициентах смещения инструмента х1+х2 = 0 начальные и делительные конусы совпадают. Этот наиболее распространенный вариант рассматривается ниже. Конусы, образующие которых перпендикулярны образующим делительных конусов (см. рис. 8.31), называют дополнительными конусами. Сечение зубьев дополнительным конусом называют торцовым сечением. Различают внешнее, внутреннее и среднее торцовые сечения. Размеры, относящиеся к внешнему торцовому сечению, сопровождают индексом е, например de, Re и др. Размеры в среднем сечении сопровождают индексом т: dnn Rm и др.; Rc и Rm — внешнее и среднее конусные расстояния, b — ширина зубчатого венца.

 

Размеры по внешнему горцу удобнее для измерения, их указывают на чертежах. Размеры в среднем сечении используют при силовых расчетах. Зависимости размеров в среднем и торцовом сечениях:

 

 

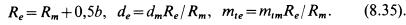
Для прямозубых передач торцовое t и нормальное и сечения совпадают. При этом mte = mne округляют до стандартного (см. табл. 8.1 ).

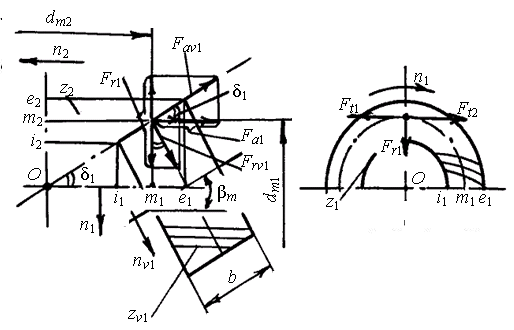
Силы в зацеплении

Рис. 13

 

1. Окружная сила (рис. 13) Ft = 2000Т / dm.

2. Радиальная сила на шестерне Fr1, равная осевой силе на колесе Fа2:

Fr1 = Fа2 = Ft (tgбncosд1 m sinвmsinд1) / cosвm. (13)

3. Осевая сила на шестерне Fа1, равная радиальной силе на колесе Fr2:

Fа1 = Fr2 = Ft (tgбnsinд1 ± sinвmcosд1) / cosвm, (14)

где в формулах (13) и (14) бn – средний нормальный угол зацепления (бn ≈ 20°); вm = 35° – средний угол наклона зуба; д1 – угол делительного конуса шестерни.

Знаки в скобках:

если смотреть с вершины делительного конуса О, то при совпадении вращения и наклона зубьев – верхние знаки, при отсутствии совпадения – нижние.

Знаки результата:

во избежание заклинивания зубьев при значительных зазорах в подшипниках необходимо обеспечить направление осевой силы Fа1 от вершины к внешнему торцу е1, т.е. сила Fа1 должна быть положительной. Это возможно при совпадении вращения и наклона зубьев.

Нормальная сила в зацеплении Fn = Ft / (cosбncosвm).

Для прямых зубьев в формулах сил следует положить вm = 0:

1) Ft1 = Ft2 = 2000Т / dm; 2) Fr1 = Fа2 = Fttgб cosд1;

3) Fа1 = Fr2 = Fttgб sinд1; 4) Fn = Ft / cosб.

Определение числа зубьев эквивалентного колеса

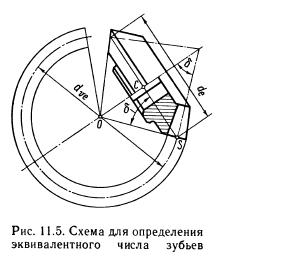
Для прямозубой передачи профили зубьев конического колеса, построенные на развертке дополнительного конуса, весьма близки к профилям зубьев эквивалентного цилин­дрического прямозубого колеса, делительная окружность которого получена разверткой допол­нительного конуса на плоскость. Дополнив развертку до полной окружности (рис. 11.5), получим эквивалентное цилиндрическое колесо с числом зубьев ζυ.

 

Из треугольника OCS (рис. 11.5) делительный диаметр эквивалентного колеса

Для передачи с круговыми зубьями профили зубьев конического колеса в нормальном сечении близки к профилям зубьев эквивалентного цилиндрического прямозубого колеса с числом зубьев Ζϋ, полученных двойным приведением: конического колеса к цилиндрическому и кругового зуба к прямому зубу [см. формулы (11.3) и (10.5ft]:

В формулах (11.3) и (11.4) ζ — действительное число зубьев конических колес.

 

 

45. Прочностной расчет конической передачи основан на допущении, что несущая способность зубьев конического колеса такая же, как и у эквивалентного цилиндрического (см. рис. 11.3), с той же длиной зуба b и профилем, соответствующим среднему дополнительному конусу (среднему сечению зубьев). Однако практика эксплуатации показала, что при одинаковой степени нагруженности конические передачи выходят из строя быстрее цилиндрических.

Проверочный расчет. Формула (9.9) в параметрах эквивалентной цилиндрической прямозубой передачи по среднему дополнительному конусу (см. рис. 11.3) имеет вид

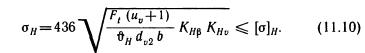
Согласно формулам (11.1) и (11.2)

Uv = dv2/dv\ = d2 cos δι/(d\ cos δ2) = = и sin 62/cos δ2 = и2.

По формуле (11.2) и табл. 11.2 dv2 = d2/cos d2 = d2 д/tg2 δ2+ 1 =d2 -\Ju2+ 1 =0,857^2 ^u2+\.

Подставив в формулу (11.10) значения Uv и dv2, получим формулу проверочного расчета для стальных конических зубчатых передачу

где Ft — в Η; de2, b — в мм; ϋΗ — коэффициент вида конических колес.

Для прямозубых колес 0//=0,85.

Для колес с круговыми зубьями:

1,85 —при твердости колеса и шестерни Н<350 НВ,

0//=1,5-при твердости колеса Н<350 НВ и шестерни Η >45 HRCa,

0//=1,3 — при твердости колеса и шестерни Η >45 HRC3;

/(яр—коэффициент, учитывающий распределение нагрузки по ширине венца.

Для прирабатывающихся колес с прямыми зубьями /С//р= 1» с круговыми зубьями /Сяр= 1,1.

Для неприрабатывающихся колес числовое значение Кн$ принимают по табл. 9.1 в зависимости от коэффициента ширины зубчатого венца

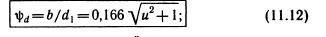
Κηό — коэффициент динамической нагрузки. Для передач с прямыми зубьями при ι; <5 м/с:

= 1,15 при твердости зубьев колеса Н<350 НВ, ΚΗό=\,\ при твердости зубьев колеса Η>350 НВ. Для передач с круговыми зубьями: Khv= 1,05 при'у^Ю м/с и любой твердости зубьев, KHv= 1,2 при t; = 10...20 м/с и твердости зубьев колеса

Η <350 НВ,

при у =10...20 м/с и твердости зубьев колеса

Η >350 НВ.

Проектировочный расчет. Заменив в формуле (11.1) значения F, = 2Т2/ (0,857de2), b = Re = 0,5ψ de2 -yfF+l/u

и решив относительно de2, запишем, окончательно получим формулу проектировочного расчета для стальных конических зубчатых передач

где de2 — внешний делительный диаметр колеса, мм; Т2— в Η•ΜΜ; [σ]// — в Н/мм2.

 

 

46. ЧЕРВЯЧНЫЕ ПЕРЕДАЧИ

Червячная передача (рис. 9.1) относится к передачам зацепления с перекрещивающимися осями валов. Угол перекрещивания обычно равен 90°. Возможны и другие углы, отличные от 90 , однако такие передачи применяют редко.

Движение в червячных передачах преобразуется по принципу винтовой пары или по принципу наклонной плоскости.

§ 9.1. Геометрические параметры и способы изготовления передач

В червячной передаче, так же как и в зубчатой, различают диаметры начальных и делительных цилиндров (рис. 9.2): dwi, dw2 -начальные диаметры червяка и колеса; du d2 - делительные диаметры червяка и колеса. В передачах без смещения dw{=dy, dw2 = d2. Точка касания начальных цилиндров является полюсом зацепления.

 

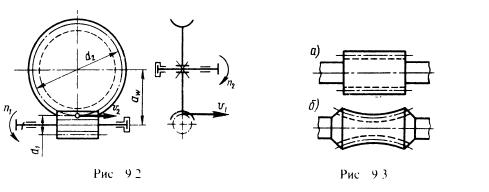
Червяки. Различают по следующим признакам: форме поверхнос ги, на которой образуе гея резьба, - - цилиндрические (рис. 9.3,(7) и глобоидные (рис. 9.3,6) ; форме профиля резьбы- -г прямолинейным (рис. 9.4. а) и криволинейным (рис. 9.4, б) профилем в осевом сечении. Наиболее распространены цилиндрические червяки. У червяков с прямолинейным профилем в осевом сечении в торцовом сечении витки очерчены архимедовой спиралью, отсюда название —архимедов червяк. Архимедов червяк подобен ходовому винту с трапецеидальной резьбой. Его можно нарезать на обычных токарных или резьбофрезерных станках. Поэтому первые червячные передачи выполняли с архимедовыми червяками, которые широко применяют и в настоящее время.

Исследования показали, что работоспособность червячной передачи повышается с уменьшением шероховатости поверхности и повышением твердости резьбы червяка (см. ниже). В последнее время все шире стали применять шлифованные высокотвердые червяки при Η ^45 HRC. Для шлифования архимедовых червяков требуются специальные шлифовальные круги фасонного профиля, что затрудняет обработку и снижает точность изготовления. Поэтому архимедовы червяки изготовляют в основном с нешлифованными витками при Η ^ 350 НВ. Для высокотвердых шлифуемых витков применяют эвольвентные червяки.

Эволъвентные червяки имеют эвольвентный профиль в торцовом сечении и, следовательно, подобны косозубым эвольвентным колесам, у которых число зубьев равно числу заходов червяка. Основное преимущество эвольвентных червяков — возможность шлифования витков плоской стороной круга. Однако для этого требуются специальные червячно-шлифовальные станки .

Способ изготовления является решающим при выборе профиля нарезки червяка, так как при одинаковом качестве изготовления форма профиля мало влияет на работоспособность передачи. Выбор профиля нарезки червяка связан также с формой инструмента для нарезания червячного колеса.

Червячное колесо нарезают червячными фрезами. Червячная фреза для нарезки червячного колеса является копией червяка. Только фреза имеет режущие кромки и наружный диаметр больше на двойной размер радиального зазора в зацеплении. При нарезании заготовка колеса и фреза совершают такое же взаимное движение, какое имеют червячное колесо и червяк в передаче. Такой метод нарезания колеса автоматически обеспечивает сопряженность профилей червяка и червячного колеса и в то же время обусловливает необходимость введения стандарта на основные геометрические параметры червяка для того, чтобы иметь ограниченный ряд стандартного инструмента.