Максимизация прибыли производителя при фиксированном объеме продукции

В случае несовершенной конкуренции фирма имеет возможность влиять на цену продукции путем варьирования выпуска своей продукции (монополия), либо на цену затрат путем варьирования своих покупок данного вида затрат (монопсония), так что

,

.

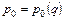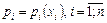Тогда задача фирмы в условиях несовершенной конкуренции может быть представлена в виде:

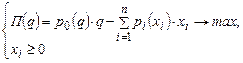
где 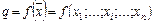есть производственная функция (выпуск фирмы).

В условиях совершенной конкуренции цена на единицу продукции фирмы не зависит от объема производства q данной фирмы, а определяется рынком и постоянна, то есть .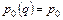

Следовательно, доход фирмы будет равен 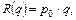доход фирмы является линейной функцией объема выпуска q.

В условиях совершенной конкуренции оптимальный уровень выпуска 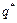является решением задачи

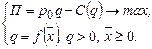
Необходимое условие экстремума функции (условие первого порядка), чтобы производная прибыли П по переменной q равнялась нулю:

.

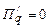Решение этого уравнения приводит к тому, что цена единицы выпуска 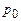равняется предельным издержкам:

.

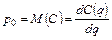Достаточное условие экстремума функции (условие второго порядка) утверждает, что предельные издержки должны возрастать в этой точке:

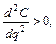
то есть кривая МС – вогнута (выпукла вниз).

Запишем прибыль производителя в общем ви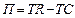де: , где 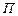– прибыль,

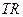– выручка,

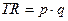– для рынка совершенной конкуренции;

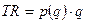– для рынка монополии;

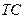– совокупные издержки, ,

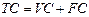где 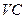– переменные издержки; 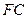– постоянные издержки.

Тогда задачу максимизации: 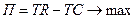решаем стандартными методами, известными из курса дисциплины «Математический анализ».

Может быть использована следующая схема решения задачи:

1) находим производную ;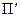

2) приравниваем ее к нулю: 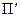= 0;

3) находим значения 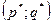– точка экстремума (проверяя, что это точка максимума);

4) 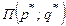– рассчитываем максимальную прибыль.

Пример 7. Общие издержки фирмы для производства продукции в объеме Q единиц определяются следующей зависимостью:

TC(Q) = 31 + 6∙Q + 5∙Q².

Фирма может реализовать любой объем произведенной продукции. При этом объем реализации продукции не влияет на рыночную цену P₀ = 216. Определить максимизирующий прибыль объем производства (Q*) и соответствующую ему величину прибыли.

Решение.

По условию задачи любой объем выпускаемой продукции фирма может продать по действующей цене. Это позволяет определить функцию валовой выручки фирмы от продажи Q ед. продукции:

TR(Q) = P₀∙Q = 216Q.

Прибыль, по определению, есть разница между валовой выручкой фирмы и общими издержками:

П(Q) = TR(Q) – TC(Q) = 216∙Q – (31 + 6∙Q + 5∙Q²) =

= 210∙Q – 31 – 5∙ Q².

Исследуем данную функцию на экстремум. Для этого найдем первую и вторую производные:

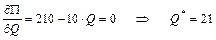
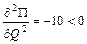, т.е. наблюдается вогнутость вверх.

Точкой глобального экстремума функции прибыли является точка Q* = 21, а вогнутость функции указывает на то, что эта точка – глобальный максимум. Таким образом, максимизирующий прибыль объем производства составляет 21 ед.

Максимальная прибыль при действующей рыночной цене составит:

П*(21) = 210∙21 – 31 – 5∙212 = 2174.

Ответ: оптимальный объем производства составляет 21 единицу, при этом прибыль максимальна и равна 2174 единицы.