 |
Главная |
Необходимые и достаточные условия сходимости ряда
|
из
5.00
|
Теория рядов.
Лекция №1.
Числовой ряд, сходимость, сумма. Основные свойства сходящихся рядов. Признаки сходимости числовых рядов.
Повторить: 1. понятие числовой последовательности;
2. арифметическую и геометрическую прогрессии;
3. технику вычисления пределов;
4. факториал;
5. сходимость несобственного интеграла.
Основные определения
Пусть дана последовательность 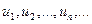 , где индексы 1,2,3…п показывают место членов последовательности.
, где индексы 1,2,3…п показывают место членов последовательности.
Определение. Сумма членов бесконечной числовой последовательности
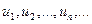 называется рядом.
называется рядом.
 (1)
(1)
При этом числа 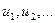 будем называть членами ряда, а un – общим членом ряда.
будем называть членами ряда, а un – общим членом ряда.
Если 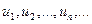 - числа, то ряд называют числовым.
- числа, то ряд называют числовым.
Если 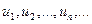 - функции, то ряд называют функциональным.
- функции, то ряд называют функциональным.
Определение. Суммы  , n = 1, 2, … называются
, n = 1, 2, … называются
частными (частичными) суммамиряда.
Таким образом, возможно рассматривать последовательности частичных сумм ряда S1, S2, … ,Sn, …
Пример 1
Записать первые три члена ряда

На практике довольно часто требуется записать несколько членов ряда.
Сначала 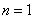 , тогда:
, тогда: 
Затем  , тогда:
, тогда: 
Потом 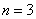 , тогда:
, тогда: 
Процесс можно продолжить до бесконечности, но по условию требовалось написать первые три члена ряда, поэтому записываем ответ: 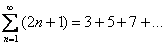
Пример 2.
Записать первые три члена ряда

подставляем в общий член ряда сначала 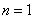 , потом
, потом  и
и 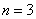 . В итоге:
. В итоге:

Ответ оставляем в таком виде, полученные члены ряда лучше не упрощать, то есть не выполнять действия:  ,
, 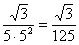 ,
,  .
.
Ответ оставим в виде 
Пример 3.
Записать сумму в свёрнутом виде с общим членом ряда

Здесь нет какого-то четкого алгоритма решения, закономерность нужно просто увидеть.
В данном случае:

Пример 4.
Записать сумму в свёрнутом виде с общим членом ряда

Пример 5.
Записать первые три члена ряда

Одной из ключевых задач теории числовых рядов является исследование ряда на сходимость. При этом возможны два случая:
Определение. Ряд  называется сходящимся, если
называется сходящимся, если
сходится последовательность его частных сумм. Сумма
сходящегося ряда – предел последовательности его частных
сумм.
 (2)
(2)
Определение. Если последовательность частных сумм ряда расходится, т.е.
не имеет предела, или имеет бесконечный предел, то ряд
называется расходящимся и ему не ставят в соответствие
никакой суммы.
· Хороший пример расходящегося числового ряда встретился в начале лекции:  .
.
Здесь совершенно очевидно, что каждый следующий член ряда – больше, чем предыдущий, поэтому  и, значит, ряд расходится. Чуть ниже мы рассмотрим более строгий математический критерий для данного примера.
и, значит, ряд расходится. Чуть ниже мы рассмотрим более строгий математический критерий для данного примера.
· В качестве примера сходящегося числового ряда можно привести
бесконечно убывающую геометрическую прогрессию, известную нам со школы:  . Сумму членов бесконечно убывающей геометрической прогрессии можно найти по формуле:
. Сумму членов бесконечно убывающей геометрической прогрессии можно найти по формуле: 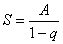 , где
, где 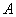 – первый член прогрессии,
– первый член прогрессии,  – основание прогрессии. В данном случае:
– основание прогрессии. В данном случае:  ,
,  . Таким образом:
. Таким образом:  . Получено конечное число, значит, ряд
. Получено конечное число, значит, ряд  сходится, что и требовалось доказать.
сходится, что и требовалось доказать.
Свойства рядов
1 свойство: Сходимость или расходимость ряда не нарушится если изменить, отбросить или добавить конечное число членов ряда.
2 свойство: Рассмотрим два ряда  и
и  , где С – постоянное число.
, где С – постоянное число.
Теорема. Если ряд  сходится и его сумма равна S, то ряд
сходится и его сумма равна S, то ряд  тоже сходится, и его сумма равна СS. (C ¹ 0)
тоже сходится, и его сумма равна СS. (C ¹ 0)
3 свойство: Рассмотрим два ряда  и
и  . Суммой или разностью этих рядов будет называться ряд
. Суммой или разностью этих рядов будет называться ряд 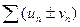 , где элементы получены в результате сложения (вычитания) исходных элементов с одинаковыми номерами.
, где элементы получены в результате сложения (вычитания) исходных элементов с одинаковыми номерами.
Теорема. Если ряды  и
и  сходятся и их суммы равны соответственно S и s, то ряд
сходятся и их суммы равны соответственно S и s, то ряд 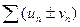 тоже сходится и его сумма равна S + s.
тоже сходится и его сумма равна S + s.

Разность двух сходящихся рядов также будет сходящимся рядом.
Сумма сходящегося и расходящегося рядов будет расходящимся рядом.
О сумме двух расходящихся рядов общего утверждения сделать нельзя.
Пусть сумма сходящего числового ряда равна S.
4 свойство: Если в ряде (1) отбросить n членов, то получим ряд  , который называется n-ым остатком ряда и обозначается
, который называется n-ым остатком ряда и обозначается  . Разность между суммой ряда S и его частичной суммой
. Разность между суммой ряда S и его частичной суммой 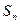 называется остатком ряда и обозначается
называется остатком ряда и обозначается  = S -
= S - 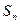 .Если ряд сходится, то остаток равен 0.
.Если ряд сходится, то остаток равен 0.
Необходимые и достаточные условия сходимости ряда
|
из
5.00
|
Обсуждение в статье: Необходимые и достаточные условия сходимости ряда |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

