 |
Главная |
Разложение в ряд Фурье
|
из
5.00
|
Лекция 2-3
Обзор анализа Фурье
Электрические сигналы связи — это меняющиеся со временем сигналы напряжения или тока, обычно описываемые во временной области. Таким способом сигнал представляется, например, на экране осциллографа. Однако, при разработке систем связи, необходимо описывать сигналы также в частотной области, где описание сигнала называется его спектром. Такая необходимость может быть проиллюстрирована следующим примером: рассмотрим систему связи с источником цифрового сигнала, выдающим прямоугольные импульсы, соответствующие передаче двоичных нуля и единицы, как показано на рис. 2.1

Рис. 2.1
Возникает вопрос: на какую частоту должны быть настроены входные цепи приемника сигнала, и в каком диапазоне частот он должен принимать такой сигнал? Ответить на него можно только представив такой сигнал в частотной области. Иначе говоря, для построения рассмотренной системы связи нужно описать, какие частоты занимает наш сигнал, а какие остаются не занятыми им.
Частотными спектральными характеристиками можно описать как сами сигналы, так и электрические схемы. Если говорится, что конкретный спектр описывает сигнал, подразумевается, что один из способов описания сигнала — это задать его амплитуду и фазу как функции частоты. В то же время, когда мы говорим о спектральных параметрах схемы, имеем в виду передаточную функцию (или частотную характеристику), связывающую выход схемы с ее входом.
Разложение в ряд Фурье
Периодические сигналы с конечной энергией, передаваемой за период, можно представить в виде ряда Фурье. Идея разложения в ряд довольно простая. При переводе сигнала из временнóй области в частотную, мы должны его как бы «измерить» в частотах. Для измерения чего-либо нам необходимо знать единицу измерения. Например, на линейке имеются деления, позволяющие определять размеры с точностью до миллиметра. Что же способно выполнять роль «засечек» в полосе частот? Известно, что гармонические колебания вида A cos wt или A sin wt происходят на одной определенной частоте. Значит, для представления сигнала в частотной области, нам нужно разложить его на эти гармонические составляющие (их называют гармониками). Скорее всего при этом окажется, что на одних частотах амплитуда сигнала больше, чем на других. Поэтому при разложении перед гармоническими функциями дописывают коэффициент пропорциональности, имеющий смысл амплитуды.
Произвольный периодический сигнал s(t)выражается через бесконечное число гармоник с возрастающими частотами.
| s(t)=½a0 + a1cos t + a2cos 2t +…+ b1sin t + b2sin 2t+… | (1) |
Функции cos t и sin t называются основными; функции cos nt и sin nt при п> 1, где п— целое, именуются гармоническими. Члены аn и bп представляют коэффициенты (амплитуды) гармоник, а 1/2а0- это постоянная составляющая.
Период функции s(t)должен быть кратным 2p.
Процесс создания произвольного периодического сигнала из коэффициентов, описывающих смешиваемые гармоники, называется синтезом. Обратный процесс вычисления коэффициентов именуется анализом.
Коэффициенты an и bn при гармонических функциях определяются по таким формулам:
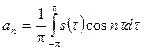
| (2) |

| (3) |
Коэффициент а0находится из (2) при п = 0. В результате получаем

| (4) |
Перепишем уравнение (1) более компактно:

| (5) |
Существует несколько способов записи пары преобразований. Наиболее распространенная форма — это выражение синуса и косинуса в экспоненциальном виде:

| (6) (7) |
Периодическая функция с периодом Т0секунд имеет следующие частотные компоненты — f0, 2f0, 3f0,..., где f0= 1/Т0 называется собственной частотой. Иногда частотные компоненты записывают как w0, 2w0, Зw0, ..., где w0 = 2p/Т0именуется собственной угловой частотой; частота f0 измеряется в герцах, частота w0 — в радианах в секунду. Заменим пt в аргументах гармонических функций в формулах (2)-(5) на 2pf0nt= 2pnt/T0, где п — целое. При п = 1, nf0 представляет собственную частоту, а при п> 1 — гармоники собственной частоты. Используя формулы (5)-(7), можно записать s(t)в экспоненциальной форме.

| (8) |
Обозначим через сn комплексные коэффициенты, или спектральные компоненты s(t), связанные с коэффициентами ап и bn следующим образом:

| (9) |
Теперь формулу (8) можно упростить.
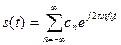
| (10) |
Здесь амплитуды экспоненциальных гармоник определяются следующим образом:

| (11) |
В общем случае коэффициент сn— комплексное число, которое можно записать следующим образом:

| (12) (13) |
где

 b0 = 0 с0 = a0/2
b0 = 0 с0 = a0/2
| (14) (15) |
Значение |сn|—амплитуда n-й гармоники периодического сигнала, так что график зависимости |сn| от частоты, называемый амплитудным спектром, дает амплитуду каждой
из п дискретных гармоник сигнала. Подобным образом график зависимости qn от частоты, именуемой фазовым спектром, дает фазу каждой гармоники сигнала.
Коэффициенты Фурье вещественной периодической по времени функции обладают следующим свойством:

| (16) |
где  — комплексно сопряженное сn. Таким образом, получаем следующее:
— комплексно сопряженное сn. Таким образом, получаем следующее:
| |c-n| = |cn| | (17) |
Амплитудный спектр является четной функцией частоты. Подобным образов фазовый спектр qn — это нечетная функция частоты, поскольку из формулы (15) следует, что
| q-n = -qn | (18) |
Интеграл Фурье
В предыдущем примере мы особо оговорили, что представляемая в виде ряда Фурье функция должна быть периодической. Однако, значительная часть используемых сигналов – непериодические. Означает ли это, что к таким сигналам преобразование Фурье неприменимо? В такой ситуации есть весьма остроумный выход. На практике мы имеем дело с сигналами, конечными во временной области. Это означает, что всякий сигнал, действительно применяемый, например, в системах связи, не передается бесконечно долго, т.е. имеет конечную длительность во времени. Обозначим ее Т0 (см. рис. 2.2).

Рис. 2.2
Поскольку за пределами Т0 сигнал отсутствует, то мы предполагаем, что это – один период периодического колебания. С математической точки зрения всякая непериодическая функция - это функция с периодом, стремящимся к бесконечности.
В этом случае число спектральных линий стремится к бесконечности. При этом суммирование спектральных составляющих становится задачей затруднительной. Однако, суммирование в таком случае может быть заменено операцией интегрирования и тогда получаем спектр частот S(f) для интегрального преобразования Фурье

| (19) |

| (20) |
где f— частота, измеряемая в герцах.
С этого момента применение прямого преобразования Фурье (19) будем обозначать Á{•}, а обратного преобразования (20) — Á-1{•}. Связь частотной и временной
областей будем указывать с использованием знака "«": s(t) « S(f).
Данная запись означает, что S(f)получается в результате применения прямого преобразования Фурье к s(t), a s(t)— в результате применения обратного преобразования Фурье к S(f). В контексте систем связи s(t)— вещественная функция, a S(f)— комплексная функция, имеющая действительный и мнимый компоненты; в полярной форме спектр S(f)можно задать через его амплитудную и фазовую характеристики.
| S(f) = |S(f)|ejq(f) | (21) |
Свойства S(f),спектра непериодического сигнала, подобны свойствам периодического сигнала; т.е. если s(t)принимает вещественные значения, то
| S(-f) = S*(f) = |S(f)|e-jq(f) | (22) |
где S* — комплексно сопряженное S. Амплитудный спектр |S(f)| — это четная функция f, а фазовый спектр — нечетная функция f. Во многих случаях функция S(f)имеет или только действительную часть, или только мнимую, так что для ее описания достаточно одного графика.
|
из
5.00
|
Обсуждение в статье: Разложение в ряд Фурье |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

