 |
Главная |
Основная теорема зацепления
|
из
5.00
|
ЛЕКЦИЯ 8
Краткое содержание
Зубчатые механизмы. Классификация зубчатых механизмов. Теоремы, определяющие кинематику высших кинематических пар. Эвольвента окружности и её свойства. Геометрические характеристики эвольвентного зубчатого колеса.
Зубчатые механизмы
Зубчатыми называют механизмы, в которых движение между звеньями (зубчатыми колесами) передаётся с помощью последовательного зацепления зубьев.
Зубчатые механизмы имеют высокие технико-экономические показатели:
· большую долговечность и надежность работы;
· высокий коэффициент полезного действия (до 0,97…0,98 для одной пары колес);
· простоту технического обслуживания;
· компактность (малые размеры и массу).
Основными недостатками являются:
· высокая трудоёмкость изготовления зубчатых колёс;
· возможность появления шума в процессе работы;
· невозможность бесступенчатого изменения передаточного отношения в процессе работы.
Классификация зубчатых механизмов
По взаимному расположению осей
· цилиндрические (имеют параллельные оси) рис.8.1, а;
· конические (оси пересекаются) рис. 8.1, б;
· гиперболоидные, червячные и винтовые (оси скрещиваются) рис. 8.1, в.
По относительному расположению поверхностей вершин и впадин зубьев колёс
· передачи внешнего зацепления (рис.8.1, а, б, в);
· передачи внутреннего зацепления (рис. 8.1 ,г).
По характеру движения осей
· обычные передачи - имеют неподвижные геометрические оси всех колёс;
· планетарные передачи - оси одного или нескольких колёс подвижны.
По направлению зубьев
· прямозубые (рис. 8.1, а, б);
· косозубые (рис. 8.1, д).
По профилю зубьев
· с эвольвентным зацеплением - профили зубьев очерчены по эвольвенте;
· с циклоидным зацеплением - профили зубьев очерчены по дугам эпи- и гипоциклоид;
· с зацеплением Новикова - профили зубьев очерчены по окружностям.
а). б). в). г). д).
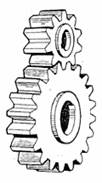




Рис.8.1
Теоремы, определяющие кинематику высших кинематических пар
Высшей кинематической парой в зубчатом механизме является кинематическая пара «зуб - зуб».
Теорема о проекциях линейных скоростей точки касания в высших кинематических парах на общую нормаль
Проекции линейных скоростей точек касания в высшей кинематической паре на общую нормаль должны быть равны между собой  . Проекции этих же скоростей на общую касательную могут отличаться как угодно
. Проекции этих же скоростей на общую касательную могут отличаться как угодно  .
.
Следствие теоремы
Концы векторов линейных скоростей точки касания должны лежать на одном перпендикуляре к общей нормали.
В случае, если  , то о
, то о  дно звено опережает другое (нарушается контакт), либо одно звено врезается в другое.
дно звено опережает другое (нарушается контакт), либо одно звено врезается в другое.
Основная теорема зацепления
Проведем через точку касания С общие касательную t-t и нормаль n-n. Покажем векторы скоростей точки касания С. При этом:  ,
, 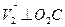 .
.
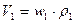 ,
, 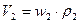 , (8.1)
, (8.1)
где  ,
,  .
.
Разложим векторы  и
и  , на составляющие: нормальные и касательные,
, на составляющие: нормальные и касательные,
Из построений следует, что 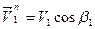 ;
;  .
.
С учетом (8.1):
(8.2)
Восстановим из точек  и
и  , перпендикуляры на нормаль
, перпендикуляры на нормаль  и
и  , которые равны:
, которые равны:
(8.3)
Подставим (8.3) в (8.2). Получим:
(8.4)
или с учетом первой теоремы:
(8.5)
Соединим центры  , и
, и  . Расстояние
. Расстояние 
 - межосевое расстояние. Точку пересечения общей нормали n - n с
- межосевое расстояние. Точку пересечения общей нормали n - n с 
 обозначим Р. Полученные треугольники
обозначим Р. Полученные треугольники  и
и  - подобны. Следовательно:
- подобны. Следовательно:
или с учетом (8.5):
(8.6)
Выражение (8.6) - основная теорема зацепления.
|
из
5.00
|
Обсуждение в статье: Основная теорема зацепления |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

