Примеры решения типовых задач

 

Примеры решения заданий даны с использованием таблицы коммутационных чисел (по общей таблице смертности) при норме доходности 5% (приложение 1).

 

Исчисление вероятностей страховых событий

 

Методические указания

Число доживающих для каждого данного возраста (Lx) показывает, сколько из 100 000 одновременно родившихся доживет до 1 года, 2 лет,..., 20,..,50,..,100 лет.

Вероятность прожить для лица, чей возраст X лет, еще 1 год (Р₄₀) составляет:

(12)

Вероятность умереть в течение предстоящего года жизни (q_x), не дожив до следующего возраста х+1 лет, свидетельствует о том, какая часть доживших до данного возраста умирает, не дожив до следующего возраста. Этот показатель представляет собой отношение числа умирающих при переходе от возраста х к возрасту х+1, т.е. (d_x) к числу доживающих до возраста x, т.е. (Lx).

(13)

Вероятность прожить X лет (nPx) равняется:

 

(14)

Вероятность умереть в течение предстоящих n лет (lnqx) равняется:

(15)

Вероятность умереть на третьем году жизни (nlqx):

(16)

 

Задание 2.1.1 Определите для лица, чей возраст 40 лет:

-вероятность прожить еще 1 год (Р₄₀);

-вероятность умереть в течение предстоящего года (q₄₀);
-вероятность прожить 3 года (₃Р₄₀);

-вероятность умереть в течение предстоящих 3 лет (l₃q₄₀);
-вероятность умереть на 3 году жизни. (₃lq₄₀);

Исходные данные представлены в табл. 2.1.

Таблица 2.1

Таблица смертности (фрагмент)

 

Возраст (х), лет	Число лиц, доживающих до возраста х лет, Lx	Число лиц, умирающих при переходе от возраста х к возрасту x+1, dx

 

Решение:

Для лица, чей возраст 40 лет, вероятность прожить еще 1 год (Р₄₀) составляет:

Вероятность умереть в течение предстоящего года жизни (q₄₀):

 

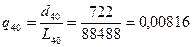
Вероятность прожить 3 года ( ) равняется:

Вероятность умереть в течение предстоящих 3 лет ( ) равняется:

Вероятность умереть на третьем году жизни (₃lq₄₀):

Расчет единовременных тарифных ставок на дожитие

Методические указания

Страховщик выплатит страховую сумму при условии дожития застрахованного до конца срока страхования. Поэтому вероятная стоимость обязательств страховщика равна произведению фактической стоимости выплаты S на вероятность ее осуществления:

(руб.), (17)

 

где nPx - вероятность дожития лица в возрасте х лет до конца срока n лет (т.е. до возраста (х + n) лет).

Поскольку выплата (если она вообще произойдет) осуществляется через n лет, то ее современная вероятная стоимость будет равна произведению вероятной стоимости на дисконтирующий множитель за n лет:

(руб.), (18)

где Vⁿ - дисконтирующий множитель за n лет.

Равенство современных вероятных стоимостей обязательств страхователя и страховщика записывается следующим образом:

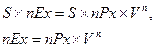(19)

Если вместо nРх подставить выражение для расчета вероятности дожития по таблице смертности, то получим общую формулу для определения единовременной нетто-ставки по страхованию на дожитие лица в возрасте x лет на срок n лет:

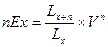, (20)

где L_x и L_x+n - показатели таблицы смертности, характеризующие численность лиц, доживающих до возраста x и (x + n) лет соответственно.

Таблица 2.2

Дисконтирующие множители (фрагмент), норма доходности 5%

 

Число лет (n)	Дисконтирующий множитель Vn
	0,95238
	0,90702
	0,86383
	0,82270
	0,78352

В соответствии с договором страхователь уплачивает взносы в начале договора страхования, а выплаты происходят через определенное время. В течение этого периода страховщик инвестирует временно свободные средства и получает на них определенный доход. Величина такого дохода, поступающего за год с единицы денежной суммы, называется нормой процента или нормой доходности. Она обозначается «i» и выражается в процентах.

Невозможность страховщика определить, под какой процент на момент страхования будут вложены взносы страхователей, предполагает применение планируемой нормы доходности. Так, если норма процента составляет 1% в год, то через год каждая денежная единица превратится в (1+i), к концу второго года эта сумма составит (1+i)Í(1+i) = (1+ i)²и т.д.

Если мы располагаем определенным денежным фондом (его величина на настоящий момент времени составляет современную стоимость этого фонда), то начисление сложных процентов за n лет рассчитывается по формуле:

 

Будущая стоимость = современная стоимость×(1 + i)ⁿ

 

Под будущей стоимостью мы понимаем размер этого фонда через n лет. В страховании жизни страховщик прогнозирует вероятную величину выплат, т.е. определяет будущую стоимость страховых фондов, необходимую через n лет. Следовательно, требуется найти размер взноса в момент заключения договора, чтобы к концу срока страхования обладать необходимыми для выплат средствами, т.е. требуется найти современную стоимость будущей выплаты. Процесс определения современной стоимости будущих доходов иди расходов называется дисконтированием и выражается следующей формулой:

Современная стоимость = будущая стоимость× (21)

Величина, обратная процентному множителю, называется
дисконтирующим множителем и обозначается через V.

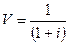(22)

Дисконтирующий множитель за ряд лет имеет вид:

(23)

 

Задание 2.2.1 Рассчитайте тарифную ставку на дожитие (₅Е₄₀) и страховой взнос.

Исходные данные:возраст человека 40 лет, срок страхования - 5 лет, норма доходности - 5%, страховая сумма 30 тыс. руб.

Решение:

Данное задание имеет 2 способа решения:

Первый способ решения:

Страховой фонд через 5 лет равен произведению страховой суммы на число доживших человек до 45 лет: 253 1370 тыс. руб. (30 тыс. руб. × 84379).

Первоначальный страховой фонд определяем с помощью дисконтирующего множителя (V⁵):1983379 тыс. руб. (253 1370 × 0,7835)

Страховой взнос определяется делением первоначальной суммы фонда на количество страхователей в возрасте 40 лет и равен 22,4 тыс. руб. (1983379/88488).

Второй способ решения:

,

где 0,7471 - тарифная ставка, умножив которую на страховую сумму, получим страховой взнос в размере 22,4 тыс. руб.