 |
Главная |
Постановка задачи и её математическая модель
|
из
5.00
|
Некоторый однородный продукт, сосредоточенный у 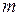 поставщиков
поставщиков  в количестве
в количестве 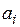
 единиц соответственно, необходимо доставить
единиц соответственно, необходимо доставить 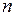 потребителям
потребителям  в количестве
в количестве 
 . Известна стоимость
. Известна стоимость  перевозки единицы груза
перевозки единицы груза 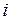 -го поставщика к
-го поставщика к 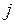 -му потребителю. Необходимо составить план перевозок, позволяющий вывезти все грузы, полностью удовлетворить потребности, и имеющий минимальную стоимость.
-му потребителю. Необходимо составить план перевозок, позволяющий вывезти все грузы, полностью удовлетворить потребности, и имеющий минимальную стоимость.
Обозначим через  количество единиц груза, запланированного к перевозке от
количество единиц груза, запланированного к перевозке от 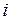 -го поставщика к
-го поставщика к 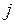 -му потребителю, тогда условие задачи можно записать в виде табл. 7.1, которую также называют матрицей планирования.
-му потребителю, тогда условие задачи можно записать в виде табл. 7.1, которую также называют матрицей планирования.
Таблица 7.1
| Поставщики | Потребители | Запасы | ||||||
| 
| 
| ||||||

| 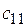
| 
| . . . | 
| 
| |||

| 
| 
| ||||||
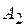
| 
| 
| . . . | 
| 
| |||

| 
| 
| ||||||
| . . . | . . . | . . . | . . . | . . . | . . . | |||

| 
| 
| . . . | 
| 
| |||

| 
| 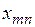
| ||||||
| Запросы | 
| 
| . . . | 
| 
|
Составим математическую модель задачи. Так как от 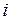 -го поставщика к
-го поставщика к 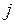 -му потребителю запланировано
-му потребителю запланировано  единиц груза, то стоимость этой перевозки составит
единиц груза, то стоимость этой перевозки составит 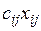 . Стоимость всего плана выразится двойной суммой
. Стоимость всего плана выразится двойной суммой  .
.
Систему ограничений получаем из следующих условий:
а) все грузы должны быть вывезены, т.е.  (эти уравнения получаются из строк);
(эти уравнения получаются из строк);
б) все потребности должны быть удовлетворены, т.е.  .
.
Таким образом, математическая модель транспортной задачи может быть записана следующим образом:
– найти минимум линейной функции
 (7.1.1)
(7.1.1)
при ограничениях

В рассматриваемой модели предполагается, что суммарные запасы равны суммарным запросам потребителей:
 . (7.1.4)
. (7.1.4)
Такая задача называется задачей с правильным балансом, а её модель – закрытой. Если же равенство (7.1.4) не выполняется, то задача называется задачей с неправильным балансом, а её модель – открытой.
Теорема 7.1. Для того чтобы транспортная задача ЛП имела решение, необходимо и достаточно, чтобы суммарные запасы поставщиков равнялись суммарным запросам потребителей (см. (7.1.4)).
Доказательство теоремы опускается.
Особенности решения транспортных задач с неправильным балансом:
1. Если суммарные запасы поставщиков превосходят суммарные запросы потребителей, т.е.
 ,
,
то необходимо ввести фиктивного (n + 1)-го потребителя с запросами

 , равными разности суммарных запасов поставщиков и запросов потребителей, и нулевыми стоимостями перевозок единиц груза
, равными разности суммарных запасов поставщиков и запросов потребителей, и нулевыми стоимостями перевозок единиц груза  .
.
2. Если суммарные запросы потребителей превосходят суммарные запасы поставщиков, т.е.
 ,
,
то необходимо ввести фиктивного (m+1)-го поставщика с запасами 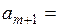
 , равными разности суммарных запросов потребителей и запасов поставщиков, и нулевыми стоимостями перевозок единиц груза
, равными разности суммарных запросов потребителей и запасов поставщиков, и нулевыми стоимостями перевозок единиц груза  .
.
3. При составлении начального опорного решения в последнюю очередь следует распределять запасы фиктивного поставщика и удовлетворять запросы фиктивного потребителя, несмотря на то, что им соответствует наименьшая стоимость перевозок, равная нулю.
7.2. Построение первоначального опорного плана
Рассмотрим систему ограничений (7.1.2) и (7.1.3) транспортной задачи. Она содержит  неизвестных и
неизвестных и  уравнений, связанных соотношением (7.1.4). Если сложить почленно отдельно уравнения подсистемы (7.1.2)
уравнений, связанных соотношением (7.1.4). Если сложить почленно отдельно уравнения подсистемы (7.1.2)
и (7.1.3), то в силу (7.1.4) получим два одинаковых уравнения, что говорит о линейной зависимости всей системы. Однако если отбросить любое из этих уравнений, то получившаяся система из  уравнений будет линейно независимой. Следовательно, опорный план транспортной задачи содержит
уравнений будет линейно независимой. Следовательно, опорный план транспортной задачи содержит  компонент перевозок. Если условия транспортной задачи и её опорный план записаны в виде таблицы (например, табл. 7.1), то клетки, в которых проставлены перевозки, называют занятыми, а остальные – незанятыми. Занятие клетки соответствует базисным переменным, и их количество также равно
компонент перевозок. Если условия транспортной задачи и её опорный план записаны в виде таблицы (например, табл. 7.1), то клетки, в которых проставлены перевозки, называют занятыми, а остальные – незанятыми. Занятие клетки соответствует базисным переменным, и их количество также равно  .
.
Однако опорный план должен удовлетворять ещё и условию ацикличности. Для того, чтобы пояснить это понятие, рассмотрим вначале следующее определение:
Определение 7.2.1. Циклом называется набор клеток таблицы транспортной задачи 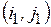 ,
,  ,
, 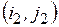 ,…,
,…,  , в которой две и только две соседние клетки содержатся в одной строке или столбце, причём последняя находится в том же столбце, что и первая.
, в которой две и только две соседние клетки содержатся в одной строке или столбце, причём последняя находится в том же столбце, что и первая.
Построение циклов начинают с какой-либо занятой клетки и переходят по столбцу(строке) к другой занятой клетке, в которой делают поворот под прямым углом и движутся по строке (столбцу) к следующей занятой клетке, пытаясь в конце концов вернуться к первоначальной. Если в построенном плане такой возврат невозможен, то план обладает свойством ацикличности и является опорным.
Первоначальный опорный план транспортной задачи как задачи ЛП можно построить ранее рассмотренными методами, что сопряжено, однако, с громоздкими вычислениями. Однако в силу специфики транспортной задачи эту проблему можно решить более простыми средствами. Существует ряд методов построения начального опорного решения. Наиболее простым из них является метод северо-западного угла.
Метод северо-западного угла. Для наглядности рассмотрим данный метод на примере. Пусть условия транспортной задачи заданы табл. 7.2.
Таблица 7.2
| Поставщики | Потребители | Запасы | |||||||||
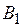
| 
| 
| 
| 
| |||||||

| |||||||||||
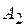
| |||||||||||

| |||||||||||

| |||||||||||
| Запросы |
Заметим, что модель задачи является закрытой. Не учитывая стоимость перевозок, заполняем клетки, начиная с 
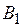 таким образом, чтобы запросы всех потребителей удовлетворялись, а запасы всех поставщиков были бы вывезены. Итак, запас 1-го поставщика – 100 единиц товара, а запрос 1-го потребителя – 200. Поэтому в первую клетку 1-го столбца заносим
таким образом, чтобы запросы всех потребителей удовлетворялись, а запасы всех поставщиков были бы вывезены. Итак, запас 1-го поставщика – 100 единиц товара, а запрос 1-го потребителя – 200. Поэтому в первую клетку 1-го столбца заносим  , исключаем из рассмотрения первого поставщика ( его запасы вывезены) и переходим ко второму поставщику, у которого 250 единиц товара. Для того, чтобы удовлетворить первого потребителя, необходимо ещё 100 единиц. Поэтому в клетку
, исключаем из рассмотрения первого поставщика ( его запасы вывезены) и переходим ко второму поставщику, у которого 250 единиц товара. Для того, чтобы удовлетворить первого потребителя, необходимо ещё 100 единиц. Поэтому в клетку 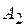
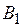 первого столбца заносим
первого столбца заносим  . Исключаем первого потребителя и переходим ко второму, запасы которого равны 200. У второго поставщика осталось 150 единиц товара, поэтому в клетку
. Исключаем первого потребителя и переходим ко второму, запасы которого равны 200. У второго поставщика осталось 150 единиц товара, поэтому в клетку 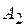
 заносим
заносим  . Исключаем из рассмотрения второго поставщика и переходим к третьему. Этот процесс продолжается до тех пор, пока остаётся неисключённой в точности одна строка или один столбец. В результате получим табл. 7.3.
. Исключаем из рассмотрения второго поставщика и переходим к третьему. Этот процесс продолжается до тех пор, пока остаётся неисключённой в точности одна строка или один столбец. В результате получим табл. 7.3.
Таблица 7.3
| Поставщики | Потребители | Запасы | |||||||||
| 
| 
| 
| 
| |||||||

| |||||||||||
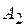
| |||||||||||

| |||||||||||

| |||||||||||
| Запросы |
Число занятых клеток  . Также легко убедиться, что заполненные клетки таблицы не образуют циклов. Следовательно, построенное решение
. Также легко убедиться, что заполненные клетки таблицы не образуют циклов. Следовательно, построенное решение 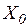 действительно является опорным.
действительно является опорным.
Замечание. Если одновременно и столбец, и строка удовлетворяют ограничениям, очередная переменная, включаемая в базисное решение, обязательно имеет нулевое значение.
Вычислим стоимость перевозки, соответствующую этому опорному плану:
 .
.
Эта стоимость перевозки на самом деле довольно далека от оптимальной, так как при составлении опорного плана не учитывались стоимости перевозок. Поэтому чаще применяют другой метод, описываемый ниже.
Метод минимальной стоимости. Данный метод позволяет построить решение, которое достаточно близко к оптимальному, так как при его применении используются стоимости транспортной задачи 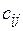
 ,
, 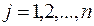 . Он состоит из ряда однотипных шагов, на каждом из которых заполняется только одна клетка, соответствующая
. Он состоит из ряда однотипных шагов, на каждом из которых заполняется только одна клетка, соответствующая  ( в отличие от метода северо- западного угла). Сам процесс заполнения клетки такой же, как и в методе северо-западного угла. Также на каждом шаге исключается из рассмотрения только одна строка (поставщик, если его запасы заканчиваются) или только один столбец (потребитель, если его запросы выполнены).
( в отличие от метода северо- западного угла). Сам процесс заполнения клетки такой же, как и в методе северо-западного угла. Также на каждом шаге исключается из рассмотрения только одна строка (поставщик, если его запасы заканчиваются) или только один столбец (потребитель, если его запросы выполнены).
Затем переходят к клетке, соответствующей  из неисключённых клеток и т.д. При этом, если поставщик ещё не исключён, но его запасы равны нулю, то на том шаге, когда от него требуется поставить груз, в соответствующую клетку таблицы заносится базисный нуль и лишь потом поставщик исключается из рассмотрения. Аналогично поступают и с потребителем.
из неисключённых клеток и т.д. При этом, если поставщик ещё не исключён, но его запасы равны нулю, то на том шаге, когда от него требуется поставить груз, в соответствующую клетку таблицы заносится базисный нуль и лишь потом поставщик исключается из рассмотрения. Аналогично поступают и с потребителем.
Рассмотрим метод минимальной стоимости на примере табл. 7.2.
Наименьшую стоимость имеет клетка 
 . Запасы 1-го поставщика, как и запросы 4-го потребителя равны 100 единицам, поэтому заносим в эту клетку 100 и исключаем, например, 4-го потребителя. Затем переходим к следующей клетке, содержащей минимальную стоимость, например, к
. Запасы 1-го поставщика, как и запросы 4-го потребителя равны 100 единицам, поэтому заносим в эту клетку 100 и исключаем, например, 4-го потребителя. Затем переходим к следующей клетке, содержащей минимальную стоимость, например, к 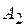
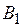 . Запасы 2-го поставщика равны 200 единицам, а запросы 1-го потребителя – 250 единиц, поэтому в клетку заносим
. Запасы 2-го поставщика равны 200 единицам, а запросы 1-го потребителя – 250 единиц, поэтому в клетку заносим  и исключаем 1-го потребителя. У 2-го поставщика остаётся ещё 50 единиц. Следующая клетка из неисключённых, соответствующая минимальной стоимости, находится на пересечении 3-й строки и 5-го столбца. Согласно тому же правилу, заносим в неё
и исключаем 1-го потребителя. У 2-го поставщика остаётся ещё 50 единиц. Следующая клетка из неисключённых, соответствующая минимальной стоимости, находится на пересечении 3-й строки и 5-го столбца. Согласно тому же правилу, заносим в неё  и исключаем 3-го поставщика и т.д. В результате получим табл. 7.4.
и исключаем 3-го поставщика и т.д. В результате получим табл. 7.4.
Таблица 7.4
| Поставщики | Потребители | Запасы | |||||||||
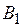
| 
| 
| 
| 
| |||||||

| |||||||||||
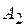
| |||||||||||

| |||||||||||

| |||||||||||
| Запросы |
Легко проверить, что полученное решение является опорным. Найдём соответствующую ему стоимость перевозок:

 .
.
Естественно возникает вопрос, является ли это решение оптимальным. Ответ на него будет дан в следующем пункте.
Метод потенциалов
Из-за громоздкости симплексных таблиц, содержащих  неизвестных, и большого объёма вычислительных работ для получения оптимального плана используются более простые методы. Самым распространённым является метод потенциалов.
неизвестных, и большого объёма вычислительных работ для получения оптимального плана используются более простые методы. Самым распространённым является метод потенциалов.
Теорема 7.3.1 (признак оптимальности опорного решения). Если план опорный  транспортной задачи является оптимальным, то ему соответствует совокупность
транспортной задачи является оптимальным, то ему соответствует совокупность 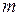 чисел
чисел  и
и 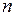 чисел
чисел  , удовлетворяющих условиям
, удовлетворяющих условиям
 (7.3.1)
(7.3.1)
для занятых клеток;
 (7.3.2)
(7.3.2)
для свободных клеток.
Доказательство теоремы см. [3, с. 618-619].
Числа 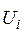 называются потенциалами поставщиков, а
называются потенциалами поставщиков, а  – потенциалами потребителей.
– потенциалами потребителей.
Замечание. Если хотя бы одна незанятая клетка не удовлетворяет условию (7.3.2), то опорный план не является оптимальным, и его можно улучшить, вводя в базис вектор, соответствующий клетке, для которой нарушается условие оптимальности (т.е. в эту клетку надо переместить некоторое количество груза).
Рассмотрим алгоритм решения транспортных задач методом потенциалов:
1. Проверить выполнение необходимого и достаточного условия разрешимости задачи. Если задача имеет неправильный баланс, то вводится фиктивный поставщик или потребитель с недостающими запасами или запросами и нулевыми стоимостями перевозок.
2. Построить начальное опорное решение (методом минимальной стоимости или каким-либо другим методом), проверить правильность его построения по количеству занятых клеток (их должно быть m + n – 1) и убедиться в линейной независимости векторов условий.
3. Построить систему потенциалов, соответствующих опорному решению. Для этого решают систему уравнений
 при xij > 0,
при xij > 0,
которая имеет бесконечное множество решений. Для нахождения частного решения системы одному из потенциалов (обычно тому, которому соответствует большее число занятых клеток) задают произвольно некоторое значение (чаще нуль). Остальные потенциалы однозначно определяются по формулам
 при xij > 0,
при xij > 0,
если известен потенциал vi , и
 при xij > 0,
при xij > 0,
если известен потенциал uj.
4. Проверить выполнение условия оптимальности для свободных клеток таблицы. Для этого вычисляют оценки для всех свободных клеток по формулам

и те из них, которые больше нуля, записывают в левые нижние углы клеток. Если для всех свободных клеток  0, то вычисляют значение целевой функции и решение задачи заканчивается, так как полученное решение является оптимальным. Если же имеется хотя бы одна клетка с положительной оценкой , опорное решение не является оптимальным.
0, то вычисляют значение целевой функции и решение задачи заканчивается, так как полученное решение является оптимальным. Если же имеется хотя бы одна клетка с положительной оценкой , опорное решение не является оптимальным.
5. Перейти к новому опорному решению, на котором значение целевой функции будет меньше. Для этого находят клетку таблицы задачи, которой соответствует наибольшая положительная оценка
 .
.
Строят цикл, включающий в свой состав данную клетку и часть клеток, занятых опорным решением. В клетках цикла расставляют поочередно знаки «+» и «–», начиная с «+» в клетке с наибольшей положительной оценкой. Осуществляют сдвиг (перераспределение груза) по циклу на величину  . Клетка со знаком «–», в которой достигается
. Клетка со знаком «–», в которой достигается  , остается пустой. Если минимум достигается в нескольких клетках, то одна из них остается пустой, а в остальных проставляют базисные нули, чтобы число занятых клеток оставалось равным m + n – 1.
, остается пустой. Если минимум достигается в нескольких клетках, то одна из них остается пустой, а в остальных проставляют базисные нули, чтобы число занятых клеток оставалось равным m + n – 1.
Далее перейти к пункту 3 данного алгоритма.
Проиллюстрируем применение указанного алгоритма на опорном плане, полученном в предыдущем примере методом наименьшей стоимости.
Шаг 1. Составим систему соотношений, соответствующих условиям (7.3.1) и (7.3.2):

Система всегда содержит  уравнений с
уравнений с  неизвестными. Уравнений на одно меньше, чем неизвестных, поэтому система является неопределённой и одному неизвестному придают произвольное значение (обычно нулевое). После этого остальные потенциалы определяются однозначно.
неизвестными. Уравнений на одно меньше, чем неизвестных, поэтому система является неопределённой и одному неизвестному придают произвольное значение (обычно нулевое). После этого остальные потенциалы определяются однозначно.
Составленный нами первоначальный опорный план содержал нулевую переменную. В этом случае обычно определяют строку, содержащую наибольшее число занятых клеток. В нашем случае это  . Положим
. Положим
 . Из последних трёх соотношений системы определяем
. Из последних трёх соотношений системы определяем  ,
,  и
и  . Из остальных уравнений получаем
. Из остальных уравнений получаем  ,
, 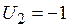 ,
,  ,
, 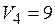 ,
,  (табл. 7.5).
(табл. 7.5).
Таблица 7.5
| Поставщики | Потребители | Запасы | |||||||||
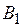

| 

| 

| 
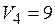
| 

| |||||||


| 
| Θ | |||||||||
  0 0
|  100 100
| ||||||||||
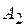
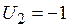
| Θ | 
| |||||||||
  50 50
|  
| ||||||||||


| |||||||||||


| 
| Θ | |||||||||
 150 150
| |||||||||||
| Запросы |
Шаг 2. Проверим условие оптимальности для незанятых клеток. Если  для всех таких клеток, то план является оптимальным, если же для некоторых
для всех таких клеток, то план является оптимальным, если же для некоторых  , то план – неоптимальный. Тогда для каждой клетки, в которой не выполняется условие оптимальности, находим величину разности
, то план – неоптимальный. Тогда для каждой клетки, в которой не выполняется условие оптимальности, находим величину разности  и записываем её значение в левый нижний угол этой клетки. Получилось 3 таких клетки:
и записываем её значение в левый нижний угол этой клетки. Получилось 3 таких клетки:  ,
,  ,
,  .
.
Шаг 3.Теперь выбираем клетку, которую необходимо сделать базисной. Загрузке подлежит, в первую очередь, клетка, которой соответствует  . В нашем случае это
. В нашем случае это  . Необходимо определить, сколько груза должно быть в неё распределено.
. Необходимо определить, сколько груза должно быть в неё распределено.
Шаг 4.Здесь необходимо выбрать клетку, которая выводится из базиса и определить величину перераспределения груза. Отмечаем знаком « + » незанятую клетку, которую надо загрузить. Вместе с ней в таблице стало  занятых клеток, следовательно, появится цикл (причём единственный), все вершины которого, за исключением клетки, находятся в занятых клетках. Начинаем движение по этому циклу от клетки, отмеченной знаком , расставляя поочерёдно во всех вершинах, в которых он меняет направление, знаки
занятых клеток, следовательно, появится цикл (причём единственный), все вершины которого, за исключением клетки, находятся в занятых клетках. Начинаем движение по этому циклу от клетки, отмеченной знаком , расставляя поочерёдно во всех вершинах, в которых он меняет направление, знаки
« – » и « + ». Затем находим  в клетках, отмеченных знаком «–». Эта величина определяет, сколько единиц груза можно перераспределить по найденному циклу. Значение
в клетках, отмеченных знаком «–». Эта величина определяет, сколько единиц груза можно перераспределить по найденному циклу. Значение 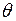 записываем в незанятую клетку, отмеченную знаком « + ». Двигаясь по циклу, вычитаем
записываем в незанятую клетку, отмеченную знаком « + ». Двигаясь по циклу, вычитаем 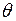 из объёмов перевозок в клетках, отмеченных знаком « – » и прибавляем к
из объёмов перевозок в клетках, отмеченных знаком « – » и прибавляем к  в клетках, отмеченных знаком « + ».
в клетках, отмеченных знаком « + ».
Итак, строим цикл, в клетку  заносим 50единиц и перераспределяем груз (табл. 7.6). Исключаем из базисных переменных
заносим 50единиц и перераспределяем груз (табл. 7.6). Исключаем из базисных переменных  и вводим
и вводим  .
.
В результате перераспределения получили новый опорный невырожденный план, который снова подлежит проверке на оптимальность. Строим ситему потенциалов:
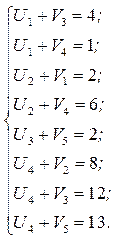
Полагая  , получим:
, получим:  ,
,  ,
,  ,
,  ,
, 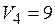 ,
,  ,
,  ,
,  .
.
Таблица 7.6
| Поставщики | Потребители | Запасы | |||||||||
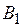

| 

| 

| 
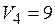
| 

| |||||||


| |||||||||||
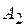

| |||||||||||


| |||||||||||


| |||||||||||
| Запросы |
Проверяя условие оптимальности, получаем, что оно выполняется во всех клетках. Следовательно, построенный план является оптимальным. Стоимость перевозки по нему 
 .
.
|
из
5.00
|
Обсуждение в статье: Постановка задачи и её математическая модель |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

