 |
Главная |
II. Нелинейное программирование
|
из
5.00
|
Нелинейное программирование— случай математического программирования, в котором целевой функцией или ограничением является нелинейная функция
Задача нелинейного программирования ставится как задача нахождения оптимума определенной целевой функции F(x1,… xn) при выполнении условий
gi(x1,…xn) ≥ 0
где xi, i=1, . . . , n — параметры, gi, j=1, . . . ,s — ограничения,n — количество параметров, s — количество ограничений.
В отличие от задачи линейного программирования, в задаче программирования нелинейного оптимум не обязательно лежит на границе области, определенной ограничениями.
Метод Фибоначчи
Постановка задачи
Требуется найти безусловный минимум функции f(x) одной переменной, т.е. такую точку  , что
, что  .
.
В методе Фибоначчи реализована стратегия, обеспечивающая максимальное гарантированное сокращение интервала неопределенности при заданном количестве вычислений функции. Эта стратегия опирается на числа Фибоначчи.
Определение. Числа Фибоначчи определяются следующим образом:
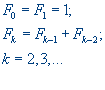 .
.
Последовательность чисел Фибоначчи имеет вид 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233,… .
Стратегия поиска.
Метод относится к последовательным стратегиям. Задается начальный интервал неопределенности и количество N вычислений функции. Алгоритм основан на анализе величин функции в двух точках. Точки вычисления функции находятся с использованием последовательности из N+1 чисел Фибоначчи. Как и в методе золотого сечения, на первой итерации требуется два вычисления функции, а на каждой последующей итерации, требуется только одно новое вычисление функции. Поиск заканчивается, когда длина текущего интервала неопределенности оказывается меньше установленной величины.
Алгоритм
Шаг 1. Задать начальный интервал неопределенности  , ], допустимую длину конечного интервала l > 0 и константу различимости
, ], допустимую длину конечного интервала l > 0 и константу различимости  .
.
Шаг 2. Найти количество N вычислений функции как наименьшее целое число, при котором удовлетворяется условие  , и числа Фибоначчи
, и числа Фибоначчи  .
.
Шаг 3. Положить k=0.
Шаг 4. Вычислить значения :
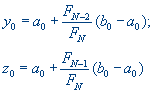 .
.
Шаг 5. Вычислить 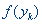 ,
,  .
.
Шаг 6. Сравнить 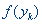 с
с 
а) если 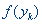

 , положить
, положить
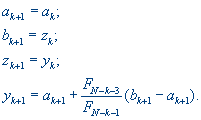
Перейти к шагу 7;
б) если 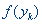 >
>  , положить
, положить
 .
.
Шаг 7. Проверить условие окончания и в случае необходимости сделать заключительное N-е вычисление функции для получения решения:
а) если  , положить k=k+1 и перейти к шагу 5;
, положить k=k+1 и перейти к шагу 5;
б) если k=N-3, то всегда  , т.е. отсутствует точка нового вычисления функции. В этом случае полагают:
, т.е. отсутствует точка нового вычисления функции. В этом случае полагают:  . В точках
. В точках  вычисляют значения функции и находят границы конечного интервала неопределенности:
вычисляют значения функции и находят границы конечного интервала неопределенности:
Если  , положить
, положить 
Если  , положить
, положить 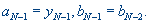
Поиск завершен и  . В качестве приближения можно взять середину этого интервала
. В качестве приближения можно взять середину этого интервала 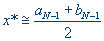 .
.
Сходимость.
Для метода Фибоначчи характеристика относительного уменьшения начального интервала неопределенности находится по формуле  , где N - количество вычислений функции.
, где N - количество вычислений функции.
|
из
5.00
|
Обсуждение в статье: II. Нелинейное программирование |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

