 |
Главная |
Уравнение второго порядка
|
из
5.00
|
Однородное уравнение второго порядка:  интегрируется следующим образом:Пусть
интегрируется следующим образом:Пусть  — корни характеристического уравнения.
— корни характеристического уравнения.  ,являющегося квадратным уравнением.
,являющегося квадратным уравнением.
Вид общего решения однородного уравнения зависит от значения дискриминанта  :при
:при  уравнение имеет два различных вещественных корня
уравнение имеет два различных вещественных корня 
Общее решение имеет вид:  при
при  — два совпадающих вещественных корня
— два совпадающих вещественных корня

Общее решение имеет вид:  при
при  существуют два комплексно сопряженных корня
существуют два комплексно сопряженных корня  Общее решение имеет вид:
Общее решение имеет вид: 
53.Линейное дифференциальное уравнение с постоянными Линейное дифференциальное уравнение с постоянными коэффициентами — обыкновенное дифференциальное уравнение вида:

где  — искомая функция,
— искомая функция,  — её
— её  -тая производная,
-тая производная,  — фиксированные числа,
— фиксированные числа,
 — заданная функция (когда
— заданная функция (когда  , имеем линейное однородное уравнение, иначе — линейное неоднородное уравнение).
, имеем линейное однородное уравнение, иначе — линейное неоднородное уравнение).
уравнение второго порядка:  интегрируется следующим образом:Пусть
интегрируется следующим образом:Пусть 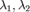 — корни характеристического уравнения.
— корни характеристического уравнения.  ,являющегося квадратным уравнением.Вид общего решения однородного уравнения зависит от значения дискриминанта
,являющегося квадратным уравнением.Вид общего решения однородного уравнения зависит от значения дискриминанта  :при
:при  уравнение имеет два различных вещественных корня
уравнение имеет два различных вещественных корня  Общее решение имеет вид:
Общее решение имеет вид:  при
при  — два совпадающих вещественных корня
— два совпадающих вещественных корня 
Общее решение имеет вид:  при
при  существуют два комплексно сопряженных корня
существуют два комплексно сопряженных корня  Общее решение имеет вид:
Общее решение имеет вид: 
54.Линейные системы с постоянными коэффициентамиСистема уравнений вида  называется неоднородной системой линейных дифференциальных уравнений с постоянными коэффициентами. Будем считать, что
называется неоднородной системой линейных дифференциальных уравнений с постоянными коэффициентами. Будем считать, что  являются непрерывными функциями на (a,b).Система дифференциальных уравнений
являются непрерывными функциями на (a,b).Система дифференциальных уравнений  называется однородной. Вводя в рассмотрение векторы
называется однородной. Вводя в рассмотрение векторы  и матрицу
и матрицу  , уравнения можно представить в векторной форме
, уравнения можно представить в векторной форме 
 Матрица
Матрица  где
где  - координаты линейно независимых решений (векторов)
- координаты линейно независимых решений (векторов) 

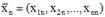
векторного уравнения ,называется фундаментальной матрицей этого уравнения. Иногда ее называют матрицей Вронского.
Определитель  составленный из частных решений системы , называется определителем Вронского. Для того, чтобы матрица , где
составленный из частных решений системы , называется определителем Вронского. Для того, чтобы матрица , где  - частные решения системы уравнений), была фундаментальной, необходимо и достаточно, чтобы
- частные решения системы уравнений), была фундаментальной, необходимо и достаточно, чтобы  при
при 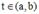 . При этом общее решение векторного уравнения представляется в виде
. При этом общее решение векторного уравнения представляется в виде  ,где C - произвольный постоянный вектор. Общее же решение уравнения будет
,где C - произвольный постоянный вектор. Общее же решение уравнения будет  где
где 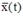 - какой-нибудь вектор, являющийся частным решением уравнения .Путем исключения неизвестных систему всегда можно свести к уравнению более высокого порядка с одной неизвестной функцией. Этот метод удобен для решений несложных систем.
- какой-нибудь вектор, являющийся частным решением уравнения .Путем исключения неизвестных систему всегда можно свести к уравнению более высокого порядка с одной неизвестной функцией. Этот метод удобен для решений несложных систем.
55Теория вероятностей - это математическая наука, изучающая закономерности случайных явлений. Под случайными явлениями понимаются явления с неопределенным исходом, происходящие при неоднократном вопроизведении определенного комплекса условий.Случайным событием (возможным событием или просто осбытием) называется любой факт который может произойти.
Под испытанием (опытом, экспериментом) в этом опредеолении понимается выполнение определенного комплекса условий, в которых наблюдается то или иное явление, фиксируется тот или иной результат.
Испытание может проводится человеком и независимо от него.
Вот примеры событий.1) Появление орла или решки на монете2) Выигрыш автомобиля по билету лотореи3) Выход бракованного изделия с конвейераСОбытие - это не какое-нибудь происшествие, а лишб возможный исхлд, результат испытания (опыта, эксперимента). События обозначаются большими буквами латинского алфавита А В или С например.
Если при каждом испытании, при котором происходит событие А, происходит и событие В, то говорят что А влечет за собой событие В(или входит в В) или В включает событие А и обозначают А⊂В. и В⊂А то в этом случае говорят, что события А и В называются  равносильными.
равносильными.
Например, если событие А - изделие 1-го сорта, В - изделие 2-го сорта, С - изделие стандартное, то А⊂С и В⊂С.Если одновременно А⊂В Элементы комбинаторикиРассмотрим некоторое множество Х, состоящее из n элементов  . Будем выбирать из этого множества различные упорядоченные подмножества
. Будем выбирать из этого множества различные упорядоченные подмножества  из k элементов.Размещением из n элементов множества Х по k элементам назовем любой упорядоченный набор
из k элементов.Размещением из n элементов множества Х по k элементам назовем любой упорядоченный набор  элементов множества Х.Если выбор элементов множества
элементов множества Х.Если выбор элементов множества  из Х происходит с возвращением, т.е. каждый элемент множества Х может быть выбран несколько раз, то число размещений из n по k находится по формуле
из Х происходит с возвращением, т.е. каждый элемент множества Х может быть выбран несколько раз, то число размещений из n по k находится по формуле  (размещения с повторениями).Если же выбор делается без возвращения, т.е. каждый элемент множества Х можно выбирать только один раз, то количество размещений из n по k обозначается
(размещения с повторениями).Если же выбор делается без возвращения, т.е. каждый элемент множества Х можно выбирать только один раз, то количество размещений из n по k обозначается  и определяется равенством
и определяется равенством  (размещения без повторений).Пример. Пусть даны шесть цифр: 1; 2; 3; 4; 5; 6. Определить сколько трехзначных чисел можно составить из этих цифр.Решение. Если цифры могут повторяться, то количество трехзначных чи сел будет
(размещения без повторений).Пример. Пусть даны шесть цифр: 1; 2; 3; 4; 5; 6. Определить сколько трехзначных чисел можно составить из этих цифр.Решение. Если цифры могут повторяться, то количество трехзначных чи сел будет  . Если цифры не повторяются,то
. Если цифры не повторяются,то  .
.
56. Классическое определение вероятности. Как было сказано выше, при большом числе n испытаний частота P*(A)=m/n появления события A обладает устойчивостью и дает приближенное значение вероятности события A, т.е.  .
.
Это обстоятельство позволяет находить приближенно вероятность события опытным путем. Практически такой способ нахождения вероятности события не всегда удобен. В ряде случаев вероятность события удается определить до опыта с помощью понятия равновероятности событий (или равновозможности). Два события называются равновероятными (или равновозможными), если нет никаких объективных причин считать, что одно из них может наступить чаще, чем другое.
Так, например, появления герба или надписи при бросании монеты представляют собой равновероятные события.
Рассмотрим другой пример. Пусть бросают игральную кость. В силу симметрии кубика можно считать, что появление любой из цифр 1, 2, 3, 4, 5 или 6 одинаково возможно (равновероятно). События E1,E2, ..., EN в данном опыте образуют полную группу, если в результате опыта должно произойти хотя бы одно из них. Так, в последнем примере полная группа событий состоит из шести событий — появлений цифр 1, 2, 3, 4, 5 и 6. Очевидно, любое событие A и противоположное ему событие  образуют полную группу. Событие B называется благоприятствующим событию A, если наступление события B влечет за собой наступление события A.
образуют полную группу. Событие B называется благоприятствующим событию A, если наступление события B влечет за собой наступление события A.
Так, если A — появление четного числа очков при бросании игральной кости, то появление цифры 4 представляет собой событие, благоприятствующее событию A. Пусть события E1,E2, ..., EN в данном опыте образуют полную группу равновероятных и попарно несовместных событий. Будем называть их исходами испытания. Предположим, что событию A благоприятствуют M исходов испытания. Тогда вероятностью события A в данном опыте называют отношение M/N. Итак, мы приходим к следующему определению.
Вероятностью P(A) события в данном опыте называется отношение числа M исходов опыта, благоприятствующих событию A, к общему числу N возможных исходов опыта, образующих полную группу равновероятных попарно несовместных событий:
 Это определение вероятности часто называют классическим. Можно показать, что классическое определение удовлетворяет аксиомам вероятности.
Это определение вероятности часто называют классическим. Можно показать, что классическое определение удовлетворяет аксиомам вероятности.
57. для определения вероятностей событий применяются не непосредственные прямые методы, а косвенные, позволяющие по известным вероятностям одних событий определять вероятности других событий, с ними связанных.Применяя эти косвенные методы, мы всегда в той или иной форме пользуемся основными теоремами теории вероятностей. Этих теорем две:• теорема сложения вероятностей;• теорема умножения вероятностей.Введем понятие о сумме событий и произведении событий.
Суммой двух событий А и В называется событие С состоящее в появлении хотя бы одного из событий А и В. Суммой нескольких событий называется событие, состоящее в появлении хотя бы одного из этих событий.Геометрическая интерпретация:
 Произведением двух событий А и В называется событие С, состоящее в совместном выполнении события А и В. Произведением нескольких событий называется событие, состоящее в совместном появлении всех этих событий.Геометрическая интерпретация:
Произведением двух событий А и В называется событие С, состоящее в совместном выполнении события А и В. Произведением нескольких событий называется событие, состоящее в совместном появлении всех этих событий.Геометрическая интерпретация:  Теорема сложения вероятностейВероятность суммы двух несовместных событий равна сумме вероятностей этих событий:Р(А+В) = Р(А) + Р(В) (1)Теорема сложения вероятностей применима к любому числу несовместных событий. В общем виде ее удобно записать:Р(∑Ai) = ∑Р(Ai) (2)Отметим следствия вытекающие из теоремы сложения вероятностей.Следствие 1: Если события А1, А2, …, Аn образуют полную группу несовместных событий, то сумма их вероятностей равна единице:∑Р(Ai) = 1 (3)Перед тем как вывести второе следствие теоремы сложения, введем понятие «противоположные события».Противоположными событиями называются два несовместных события, образующих полную группу. Событие противоположное событию А принято обозначать A.Пример:
Теорема сложения вероятностейВероятность суммы двух несовместных событий равна сумме вероятностей этих событий:Р(А+В) = Р(А) + Р(В) (1)Теорема сложения вероятностей применима к любому числу несовместных событий. В общем виде ее удобно записать:Р(∑Ai) = ∑Р(Ai) (2)Отметим следствия вытекающие из теоремы сложения вероятностей.Следствие 1: Если события А1, А2, …, Аn образуют полную группу несовместных событий, то сумма их вероятностей равна единице:∑Р(Ai) = 1 (3)Перед тем как вывести второе следствие теоремы сложения, введем понятие «противоположные события».Противоположными событиями называются два несовместных события, образующих полную группу. Событие противоположное событию А принято обозначать A.Пример:
Событие А – безотказная работа всех элементов технической системы; A – отказ хотя бы одного элемента.Следствие 2: Сумма вероятностей противоположных событий равна единице:P(A) + P(A) =1 (4)Следствие 2 есть частный случай следствия 1.
Вероятность суммы двух совместных событий выражается формулой:Р(А+В) = Р(А) + Р(В) – P(AB) (5)Аналогично вероятность суммы трех совместных событий вычисляется по формуле:Р(А+В+С) = Р(А) + Р(В) + Р(С) – P(AB) – P(AС) – P(ВС) + Р(АВС) (6)
Общая формула для вероятности суммы любого числа совместных событий:
Р(∑Ai) = ∑Р(Ai) – ∑Р(AiAj) + ∑Р(AiAjAk) – (-1)n-1P(A1A2…An) (7)где суммы распространяются на различные значения индексов i; i, j; i, j, k и т.д.Из формул (5) и (6) можно записать аналогичную формулу для произведения событийP(AB) = Р(А) + Р(В) – Р(А+В) (8)
Р(АВС) = Р(А) + Р(В) + Р(С) – P(A+B) – P(A+С) – P(В+С) + Р(А+В+С) (9)
Теорема умножения вероятностейВведем понятие независимые и зависимые события.Событие А называется независимым от события В, если вероятность события А не зависит от того, произошло событие В или нет.Событие А называют зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.Вероятность события А, вычисленная при условии, что имело место другое событие В, называется условной вероятностью события А и обозначается Р (А/В)Теорема умножения: Вероятность произведения двух событий равна произведению вероятностиР(АВ) = P(A)×Р(В/А) (12)Вероятность произведения нескольких событий равна произведению вероятностей этих событий, причем вероятность каждого следующего по порядку события вычисляется при условии, что все предыдущие имели место:Р(А1А2…Аn ) = P(A1)×Р(А2/А1)×Р(А3/А1А2)×…×Р(Аn/А1А2…А n-1) (13)Следствие1: Если событие А не зависит от события В, то и событие В не зависит от события АСледствие2: Вероятность произведения двух независимых событий равна произведению вероятностей этих событийP(AВ) = P(А)×Р(В) (14) Р(А1А2…Аn ) = P(A1)×Р(А2)×….×Р(Аn) (15)Формула полной вероятности:Следствием основных теорем является так называемая формула полной вероятности.Пусть требуется определить вероятность некоторого события А, которое может произойти вместе с одним из событий:
Н1, Н2, ….Нn,Образующих полную группу несовместных событий. Будем эти события называть гипотезами.В этом случае, вероятность события А вычисляется как сумма произведений вероятности каждой гипотезы на вероятность события при этой гипотезеР(А)=∑Р(Hi)×P(A/Hi) (16)
58Формула полной вероятности.
Пусть событие A может произойти только вместе с одним из попарно несовместных событий H1, H2, ..., Hn, образующих полную группу. Тогда, если произошло событие A, то это значит, что произошло одно из попарно несовместных событий H1A, H2A, ..., HnA. Следовательно,  Применяя аксиому сложения вероятностей, имеем
Применяя аксиому сложения вероятностей, имеем  Но
Но  (i=1, 2, ..., n), поэтому
(i=1, 2, ..., n), поэтому

|
Эта формула называется формулой полной вероятности. События H1, H2, ..., Hn часто называют «гипотезами».
Теорема гипотез (формула Бейеса)Имеется полная группа несовместных гипотез Н1, Н2, …., Нn. Вероятности этих гипотез до опыта известны и равны соответственно Р(Н1), Р(Н2)…. Р(Нn).Произведен опыт, в результате которого наблюдалось появление некоторого события А. Как следует изменить вероятность гипотез в связи с появлением этого события? По существу речь идет о том, чтобы найти условную вероятность Р(Нi/А) для каждой гипотезы.Р(Нi/А) = [Р(Нi)×Р(Нi/A] / [∑Р(Hi)×P(A/Hi)], i = 1, 2, …, n (17)
59. Теорема о повторении опытов. Формула Бернулли.ПОВТОРЕНИЕ НЕЗАВИСИМЫХ ОПЫТОВ. Несколько опытов называются независимыми, если вероятность исхода опыта не зависит от того, какие исходы имели другие опыты. Рассмотрим случай, когда вероятности исходов опытов постоянны и не зависят от номера опыта.Пусть один тот же опыт проводятся n раз. В каждом опыте некоторые события А1, А2, …, Аr появляется с вероятностями р1, р2, …, рп. Будем рассматривать не результат каждого конкретного опыта, а общее число появлений событий А1, А2, …, Аr .Рассмотрим случай с двумя возможными исходами опытов, т.е. в результате каждого опыта событие Aпоявляется с вероятностью р и не появляется с вероятностью q=1-p. Вероятность P(n,k) того, что в последовательности из n опытов интересующее нас событие произойдет ровно k раз (безразлично, в какой последовательности), равна (формула Бернулли) 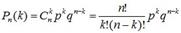 Следствия из формулы Бернулли.1Вероятность того, что событие А наступит менее k раз
Следствия из формулы Бернулли.1Вероятность того, что событие А наступит менее k раз  2Вероятность того, что событие наступит более k раз
2Вероятность того, что событие наступит более k раз
 3Вероятность того, что в n опытах схемы Бернулли, событие А появится от k1 до k2 раз
3Вероятность того, что в n опытах схемы Бернулли, событие А появится от k1 до k2 раз  4Вероятность того, что в n опытах событие А появится хотя бы один раз, определяется формулой
4Вероятность того, что в n опытах событие А появится хотя бы один раз, определяется формулой  Число к0, которому соответствует максимальная биномиальная вероятность
Число к0, которому соответствует максимальная биномиальная вероятность  , называетсянаивероятнейшим числом появления события А. При заданных n и p это число определяется неравенствами:
, называетсянаивероятнейшим числом появления события А. При заданных n и p это число определяется неравенствами:  .
.
60. Определение Пусть  — вероятностное пространство. Функция
— вероятностное пространство. Функция  , измеримая относительно
, измеримая относительно  иборелевской σ-алгебры на
иборелевской σ-алгебры на  , называется случайной величиной.Вероятностное поведение случайной величины полностью описывается её распределением.Простейшие обобщения Случайная величина, вообще говоря, может принимать значения в любом измеримом пространстве. Тогда её чаще называют случайным вектором или случайным элементом. Например,1Измеримая функция
, называется случайной величиной.Вероятностное поведение случайной величины полностью описывается её распределением.Простейшие обобщения Случайная величина, вообще говоря, может принимать значения в любом измеримом пространстве. Тогда её чаще называют случайным вектором или случайным элементом. Например,1Измеримая функция  называется n-мерным случайным вектором (относительно борелевской σ-алгебры на
называется n-мерным случайным вектором (относительно борелевской σ-алгебры на  ).2Измеримая функция
).2Измеримая функция  называется n-мерным комплексным случайным вектором (также относительно соответствующей борелевской σ-алгебры).3Измеримая функция, отображающая вероятностное пространство в пространство подмножеств некоторого (конечного) множества, называется (конечным) случайным множеством.
называется n-мерным комплексным случайным вектором (также относительно соответствующей борелевской σ-алгебры).3Измеримая функция, отображающая вероятностное пространство в пространство подмножеств некоторого (конечного) множества, называется (конечным) случайным множеством.
Распределение вероятностей — это закон, описывающий область значений случайной величины и вероятности их принятия.Определение 1. Пусть задано вероятностное пространство  , и на нём определена случайная величина
, и на нём определена случайная величина  . В частности, по определению,
. В частности, по определению,  является измеримым отображением измеримого пространства
является измеримым отображением измеримого пространства  в измеримое пространство
в измеримое пространство  , где
, где  обозначает борелевскую сигма-алгебру на
обозначает борелевскую сигма-алгебру на  . Тогда случайная величина
. Тогда случайная величина  индуцирует вероятностную меру
индуцирует вероятностную меру  на
на  следующим образом:
следующим образом:  Мера
Мера  называется распределением случайной величины
называется распределением случайной величины  . Иными словами,
. Иными словами,  , таким образом
, таким образом 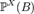 задаёт вероятность того, что случайная величина
задаёт вероятность того, что случайная величина  попадает во множество
попадает во множество  .Способы задания распределенийОпределение 2. Функция
.Способы задания распределенийОпределение 2. Функция  называется (кумулятивной) функцией распределения случайной величины
называется (кумулятивной) функцией распределения случайной величины  . Из свойств вероятности вытекает:Теорема 1. Функция распределения
. Из свойств вероятности вытекает:Теорема 1. Функция распределения  любой случайной величины удовлетворяет следующим трем свойствам:1
любой случайной величины удовлетворяет следующим трем свойствам:1  — функция неубывающая;2
— функция неубывающая;2  ; 3
; 3  непрерывна слева.Из того факта, что борелевская сигма-алгебра на вещественной прямой порождается семейством интервалов вида
непрерывна слева.Из того факта, что борелевская сигма-алгебра на вещественной прямой порождается семейством интервалов вида  , вытекаетТеорема 2. Любая функция
, вытекаетТеорема 2. Любая функция  , удовлетворяющая трём свойствам, перечисленным выше, является функцией распределения для какого-то распределения
, удовлетворяющая трём свойствам, перечисленным выше, является функцией распределения для какого-то распределения  .Для вероятностных распределений, обладающих определенными свойствами, существуют более удобные способы его задания.Дискретные распределения/ Определение 3. Случайная величина называется простой или дискретной, если она принимает не более, чем счётное число значений. То есть
.Для вероятностных распределений, обладающих определенными свойствами, существуют более удобные способы его задания.Дискретные распределения/ Определение 3. Случайная величина называется простой или дискретной, если она принимает не более, чем счётное число значений. То есть  , где
, где  — разбиение
— разбиение  .Распределение простой случайной величины тогда по определению задаётся:
.Распределение простой случайной величины тогда по определению задаётся:  . Введя обозначение
. Введя обозначение  , можно задать функцию
, можно задать функцию  . Очевидно, что
. Очевидно, что  . Используя счётную аддитивность
. Используя счётную аддитивность  , легко показать, что эта функция однозначно определяет распределение
, легко показать, что эта функция однозначно определяет распределение  Определение 4. Функция
Определение 4. Функция  , где
, где  часто называется дискретным распределением.
часто называется дискретным распределением.
Теорема 3. Дискретное распределение обладает следующими свойствами:1.  ;2.
;2.  .Непрерывные распределенияНепрерывное распределение — распределение вероятностей, не имеющее атомов. Любое распределение вероятностей есть смесь дискретного и непрерывного.Абсолютно непрерывные распределенияОпределение 5. Распределение случайной величины
.Непрерывные распределенияНепрерывное распределение — распределение вероятностей, не имеющее атомов. Любое распределение вероятностей есть смесь дискретного и непрерывного.Абсолютно непрерывные распределенияОпределение 5. Распределение случайной величины 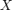 называется абсолютно непрерывным, если существует неотрицательная функция
называется абсолютно непрерывным, если существует неотрицательная функция  , такая что
, такая что  . Функция
. Функция  тогда называется плотностью распределения случайной величины
тогда называется плотностью распределения случайной величины  .
.
Теорема 4. Если функция  такая, что:1
такая, что:1  ;2
;2 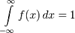 ,то существует распределение
,то существует распределение  такое, что
такое, что  является его плотностью.Просто применение формулы Ньютона-Лейбница приводит к простому соотношению между кумулятивной функцией и плотностью абсолютно непрерывного распределения.Теорема 5. Если
является его плотностью.Просто применение формулы Ньютона-Лейбница приводит к простому соотношению между кумулятивной функцией и плотностью абсолютно непрерывного распределения.Теорема 5. Если 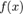 — непрерывная плотность распределения, а
— непрерывная плотность распределения, а  — его кумулятивная функция, то1
— его кумулятивная функция, то1  2
2  .
.
61 Функция распределения вероятностей случайной величины и ее свойства.
Рассмотрим функцию F(х), определенную на всей числовой оси следующим образом: для каждого х значение F(х) равно вероятности того, что дискретная случайная величина  примет значение, меньшее х, т. е.
примет значение, меньшее х, т. е. 
Эта функция называется функцией распределения вероятностей, или кратко, функцией распределения. Зная функцию распределения F(x), легко найти вероятность того, что случайная величина  удовлетворяет неравенствам
удовлетворяет неравенствам  .
.
Рассмотрим событие, заключающееся в том, что случайняя величина примет значение, меньшее  . Это событие распадается на сумму двух несовместных событий: 1) случайная величина
. Это событие распадается на сумму двух несовместных событий: 1) случайная величина  принимает значения, меньшие
принимает значения, меньшие  , т.е.
, т.е.  ; 2) случайная величина
; 2) случайная величина  принимает значения, удовлетворяющие неравенствам
принимает значения, удовлетворяющие неравенствам  . Используя аксиому сложения, получаем
. Используя аксиому сложения, получаем
 Отсюда
Отсюда 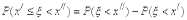 Но по определению функции распределения F(x) , имеем
Но по определению функции распределения F(x) , имеем  ,
, 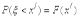 ; cледовательно,
; cледовательно,  Таким образом, вероятность попадания дискретной случайной величины в интервал
Таким образом, вероятность попадания дискретной случайной величины в интервал  равна приращению функции распределения на этом интервале.
равна приращению функции распределения на этом интервале.
Рассмотрим основные свойства функции распределения.
1°. Функция распределения является неубывающей. В самом деле, пусть  <
<  . Так как вероятность любого события неотрицательна, то
. Так как вероятность любого события неотрицательна, то  . Поэтому из формулы (19) следует, что
. Поэтому из формулы (19) следует, что  , т.е.
, т.е.  .
.
2°. Значения функции распределения удовлетворяют неравенствам 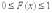 .
.
Это свойство вытекает из того, что F(x) определяется как вероятность [см. формулу (18)]. Ясно, что  и
и  .
.
3°. Вероятность того, что дискретная случайная величина  примет одно из возможных значений xi, равна скачку функции распределения в точке xi. Действительно, пусть xi - значение, принимаемое дискретной случайной величиной, и
примет одно из возможных значений xi, равна скачку функции распределения в точке xi. Действительно, пусть xi - значение, принимаемое дискретной случайной величиной, и  . Полагая в формуле (19)
. Полагая в формуле (19)  ,
,  , получим
, получим  В пределе при
В пределе при  вместо вероятности попадания случайной величины на интервал
вместо вероятности попадания случайной величины на интервал  получим вероятность того, что величина
получим вероятность того, что величина  примет данное значение xi:
примет данное значение xi:  C другой стороны, получаем
C другой стороны, получаем  , т.е. предел функции F(x) справа, так как
, т.е. предел функции F(x) справа, так как  . Следовательно, в пределе формула (20) примет вид
. Следовательно, в пределе формула (20) примет вид

|
т.е. значение p(xi) равно скачку функции ** xi.
62.Функция распределения плотности вероятностей и ее свойства.Из формулы P{Α ≤ X < Β}=F(Β)-F(Α)следует, что вероятность попадания случайной величины в заданный интервал определяется скоростью изменения функции распределения вероятностей на этом интервале. Скорость изменения непрерывной функции равна ее производной. Это позволяет ввести новую функцию для задания случайной величины. Рассмотрим снова вероятность попадания случайной величины в интервал [x,x+Δx]:P{x≤X<x+Δx}=F(x+Δx)-F(x).Пусть Х - непрерывная случайная величина. Тогда для малых значений Δx эта вероятность будет также достаточно малой. Поделим ее на Δx и перейдем к пределу при Δx →0:limΔx →0(P{x≤X<x+Δx}/Δx)=limΔx →0(F(x+Δx)-F(x))/Δx).Если это предел существует, то он равен производной от функции распределения F(x): limΔx →0(F(x+Δx)-F(x))/Δx)=F'(x)=f(x).Функция f(x) называется плотностью распределения вероятностей случайной величины Х. Из определения следует, что при малых значениях Δx справедливо равенство: P{x≤X<x+Δx}≈f(x)*ΔxРассмотрим свойства плотности распределения f(x).1. Всегда f(x)≥0, так как функция F(x) является неубывающей функцией.2 Для функции распределения F(x) справедливо равенство:F(x)=-∞∫xf(t)dt.Действительно, так как по определению f(x)=F'(x), то F(x) является первообразной функцией по отношению к плотности распределения f(x). Следовательно,
-∞∫∞f(t)dt=F(t)-∞ιx=F(x)-F(-∞)=F(x)-0=F(x.)3. Вероятность попадания случайной величины в заданный интервал [Α ; Β] равна: P{Α≤X<Β}=Α∫βf(t)dt.Действительно, в соответствии с формулой Ньютона-Лейбница этот определенный интеграл равен F(Β)-F(Α). По 3-му свойству функции распределения вероятностей эта разность и представляет собой вероятность P{Α≤X<Β} .4. Интеграл от плотности распределения вероятности по всей области задания случайной величины равен единице: -∞∫∞f(t)dt=1 .Равенство -∞∫∞f(t)dt=1 представляет условие нормировки вероятностей для непрерывных случайных величин. По смыслу данный интеграл есть не что иное, как F(∞)=1. Условие нормировки вероятностей часто используется для определения неизвестного параметра закона распределения.Для иллюстрации геометрического смысла перечисленных свойств приведем пример графика плотности распределения вероятностей. Для большей наглядности на рис. представлен также график соответствующей функции  распределения вероятностей.
распределения вероятностей.
 Вся кривая плотности распределения вероятностей располагается выше оси 0Х (свойство1), причем максимум плотности достигается в точке х=а, в которой функция распределения вероятностей имеет наибольшую крутизну. Вероятность попадания случайной величины в интервал [Α ; Β] численно равна площади криволинейной трапеции, построенной на этом интервале как на основании и ограниченной сверху графиком плотности распределения (заштрихованная на рисунке область). Площадь всей криволинейной трапеции, заключенной между осью 0Х и графиком плотности распределения, всегда равна единице. Любая функция, удовлетворяющая перечисленным выше свойствам, может быть плотностью распределения некоторой непрерывной случайной величины.
Вся кривая плотности распределения вероятностей располагается выше оси 0Х (свойство1), причем максимум плотности достигается в точке х=а, в которой функция распределения вероятностей имеет наибольшую крутизну. Вероятность попадания случайной величины в интервал [Α ; Β] численно равна площади криволинейной трапеции, построенной на этом интервале как на основании и ограниченной сверху графиком плотности распределения (заштрихованная на рисунке область). Площадь всей криволинейной трапеции, заключенной между осью 0Х и графиком плотности распределения, всегда равна единице. Любая функция, удовлетворяющая перечисленным выше свойствам, может быть плотностью распределения некоторой непрерывной случайной величины.
63. Числовые характеристики случайных величин и их свойстваЧисловыми характеристиками случайных величин являются математическое ожидание и дисперсия, а так же и моменты случайных величин.Математическое ожиданием М(Х) называется средняя величина возможных значений случайных величин, взвешенных по их вероятности. Выражается формулой:
 Свойство 1. Мат. ожидание постоянной равно этой постоянной.Свойство 2. Мат. ожидание суммы случайных величин равно сумме их мат. ожиданий:
Свойство 1. Мат. ожидание постоянной равно этой постоянной.Свойство 2. Мат. ожидание суммы случайных величин равно сумме их мат. ожиданий:  Из этого свойства следует следствие:
Из этого свойства следует следствие:
Математическое ожидание суммы конечного числа случайных величин равно сумме их математических ожиданий:

Свойство 3. Математическое ожидание произведения независимых случайных величин Х и Yравно произведению математических ожиданий этих вел. M(XY)=M(X)·(M)Y.
Следствие. Постоянный множитель можно вынести за знак математических ожидания: М(сХ) = сМ(Х)
Дисперсией называется математическое ожидание квадрата отклонения случайных величин от математического ожидания:
D[Х]=M[X-M(X)]2
Свойство 1. Дисперсия постоянной величины равна нулю.
Свойство 2. постоянную величину можно вынести за знак дисперсии, предварительно возведя ее в квадрат:
D(cX) = c2D(X)
Свойство 3. Дисперсия суммы независимых случайных величин Х и Y равна сумме их дисперсий:
D(X+Y) = D(X) + D(Y), от сюда следствие:если х1, х2,..., хn - случайные величины, каждая из которых независима от суммы остальных, то
D(X1+X2+...+Xn) = D(X1) + D(X2)+...+D(Xn).
Моментом k-порядка называется математическое ожидание k-й степени отклонения случайнойвеличины Х от некоторой постоянной с.
Если в качестве с берется нуль, моменты называются начальными
νk = М(Х)k
Если с = М(Х), то моменты называются центральными
μ = M[X – M(X)]k
|
из
5.00
|
Обсуждение в статье: Уравнение второго порядка |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

