Числовой ряд и его сходимость

Пусть задана бесконечная последовательность чисел …

Тогда + +… +…= 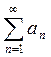(1) называется числовым рядом, а числа -члены ряда,

-общий член ряда.

2.Сумма ряда. Примеры сходящихся и расходящихся рядов. Гармонический ряд (док-во его расходимости).

Сумма вида =

= + = +

= + +… = +

Называется частичными суммами ряда 1,

а последовательность (2) называется последовательность частичных сумм ряда (1)

Ряд (1) называется сходящимся,если сходится последовательность его частичных сумм(2)

Т.е если =S

При этом число S называется суммой ряда (1)

А если = или не существует то ряд (1) назыв-ся расходящимся

Примеры рядов:

• расходится

• сходится

• = сходится только если /q/<1 =>S= ,q≠0

Доказательство расходимости гармонического ряда по Коши: f(x)=1/x

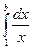= = (lnx) = (lnB*0),где lnB→

Свойства сходящихся рядов

Пусть задан ряд

(1) и если в ряде 1 отбросить первые n членов ,

то получим ряд (3) = + +…+ … 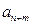который называется остатком ряда (1)

ТЕОРЕМА:

Ряд 1 и его остаток-ряд 3 сходятся или расходятся одновременно.

ДОКАЗАТЕЛЬСТВО:

Пусть -частичная сумма ряда 1 ,а -частичная сумма ряда 3. ТО = +

= ( + ) и последний предел существует,если существует предел .

СЛЕДСТВИЕ:

Если в ряде 1 отбросить конечное число членов,то это не влияет на сходимость ряда.

Теорема:

Для того чтобы ряд 1 сходился необходимо и достаточно!

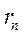=0

Где = + +…+

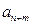
Сходящиеся ряды можно:

-умножать на одно и тоже число

-почленно складывать и вычитать

Необходимый признак сходимости ряда (док-во).

Теорема:

Еслди ряд 1 сходится,то его ый член стремится к нулю,т.е =0

Доказательство.

Пусть ряд S- сумма ряда 1(т.к по условию ряд сходится).т.е =S

= - = -

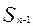
Следствие: если не стремится к 0 ,при n→ , ряд 1 расходится

Теорема Абеля.

1) Если степенной ряд a_nxⁿ сходится при x=x₀, то он сходится причем абсолютно для всех x , удовлетворяющих неравенству |x|<|x₀|

2) Если же ряд a_nxⁿ расходится при x=x_{1 ,} то он расходится при всех x , удовлетворяющих условию |x|>|x₁|

Док-во (основано на свойствах последовательностей).

1)Так как числовой ряд a_nx₀ⁿ сходится, то a_nx₀ⁿ =0. Это означает, что числовая последовательность {a_nx₀ⁿ} ограничена.Тогда перепишем степенной ряд в виде

a₀ + a₁x₀ (x/x₀) + a₂x₀²(x²/x₀²) +…+…= 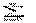a_nx₀ⁿ (x/x₀)²

Рассмотрим ряд из абсолютных величин.

|a₀| + |a₁x₀ (x/x₀) | + |a₂x₀²(x²/x₀²) | +…+…<= M + M| x/x₀| + M| x/x₀|² +…= M(1+q+ q²+…)

Это геометрическая прогрессия с q=(x/x₀)<1—сходится. Из признака сравнения следует абсолютная сходимость степенного ряда.

2) 2-ая часть теоремы. От противного. Пусть степенной ряд сходится при некотором x^*, | x^*|> x_1. Но тогда согласно 1-ой части теоремы, степенной ряд сходится для всех | x |< x^* . В том числе должен сходится

и при x= x₀, так как | x |< | x^*| . Но это противоречит

предположению теоремы. Теорема доказана.