 |
Главная |
Уравнение теплопроводности. Интеграл Пуассона
|
из
5.00
|
Температуру физического тела в произвольной точке с координатами (x, y, z) в момент времени t можно представить в виде функции:

Составим дифференциальное уравнение:

Выражение  называется оператором Лапласа.
называется оператором Лапласа.
Тогда составленное нами дифференциальное уравнение принимает вид:

и называется уравнением теплопроводности в пространстве.
В качестве частных случаев рассматривают:
 - уравнение теплопроводности в стержне,
- уравнение теплопроводности в стержне,
 - уравнение теплопроводности на плоскости.
- уравнение теплопроводности на плоскости.
В случае рассмотрения уравнения теплопроводности в стержне искомая функция u(x, t) должна удовлетворять записанному выше дифференциальному уравнению, начальному условию 
 и граничным условиям
и граничным условиям  .
.
В результате решения дифференциального уравнения методом Фурье получим:

Отметим, что распространение тепла в теле называется стационарным, если функция u не зависит от времени t.
Интеграл Пуассона
Интегра́л Пуассо́на позволяет получить решение задачи Дирихле для уравнения Лапласа в шаре.
Пусть для гармонической в шаре функции u(r, φ) поставлено условие равенства на границе функции u0: u(R, φ) = u0(φ), при этом функции принадлежат следующим классам гладкости:  , где ∂D — граница шара D, а
, где ∂D — граница шара D, а  — его замыкание. Тогда решение такой задачи Дирихле представимо в виде интеграла Пуассона:
— его замыкание. Тогда решение такой задачи Дирихле представимо в виде интеграла Пуассона:

где ωn — площадь единичной сферы, а n — размерность пространства.
Вывод формулы в двумерном случае
Известно, что функция

является решением задачи Дирихле для уравнения Лапласа в круге. Преобразуем это выражение с учётом выражений для коэффициентов Фурье:



Последнюю сумму можно вычислить при 0≤r<R:


Таким образом, в преобразованном виде интеграл Пуассона для круга приобретает вид:

Уравнение Эйлера для функционала Лагранжа
Пусть задан функционал 
с подынтегральной функцией  , обладающей непрерывными первыми частными производными и называемой функцией Лагранжа или лагранжианом, где через f' обозначена первая производная f по x. Если этот функционал достигает экстремума на некоторой функции
, обладающей непрерывными первыми частными производными и называемой функцией Лагранжа или лагранжианом, где через f' обозначена первая производная f по x. Если этот функционал достигает экстремума на некоторой функции  , то для неё должно выполняться обыкновенное дифференциальное уравнение
, то для неё должно выполняться обыкновенное дифференциальное уравнение 
которое называется уравнением Эйлера — Лагранжа.
Доказательство
Вывод одномерного уравнения Эйлера — Лагранжа является одним из классических доказательств в математике. Оно основывается на основной лемме вариационного исчисления.
Мы хотим найти такую функцию  , которая удовлетворяет граничным условиям
, которая удовлетворяет граничным условиям  ,
,  и доставляет экстремум функционалу
и доставляет экстремум функционалу 
Предположим, что  имеет непрерывные первые производные. Достаточно и более слабых условий, но доказательство для общего случая более сложно.
имеет непрерывные первые производные. Достаточно и более слабых условий, но доказательство для общего случая более сложно.
Если  даёт экстремум функционалу и удовлетворяет граничным условиям, то любое слабое возмущение
даёт экстремум функционалу и удовлетворяет граничным условиям, то любое слабое возмущение  , которое сохраняет граничные условия, должно увеличивать значение
, которое сохраняет граничные условия, должно увеличивать значение  (если
(если  минимизирует его) или уменьшать
минимизирует его) или уменьшать  (если
(если  максимизирует).
максимизирует).
Пусть  — любая дифференцируемая функция, удовлетворяющая условию
— любая дифференцируемая функция, удовлетворяющая условию  . Определим
. Определим

Поскольку  даёт экстремум для
даёт экстремум для  , то
, то  , то есть
, то есть

Интегрируя по частям второе слагаемое, находим, что 
Используя граничные условия на  , получим
, получим 
Отсюда, так как  — любая, следует уравнение Эйлера — Лагранжа:
— любая, следует уравнение Эйлера — Лагранжа:
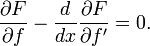
|
из
5.00
|
Обсуждение в статье: Уравнение теплопроводности. Интеграл Пуассона |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

