Однородные уравнение первого уравнения

Дифференциальное уравнение вида называется однородным дифференциальным уравнением первого порядка, если функция f(x,y) может быть представлена в виде

. (8.6)

В этом случае вводится новая переменная или , откуда и исходное дифференциальное уравнение преобразуется к виду

Таким образом, получили уравнение с разделяющимися переменными относительно неизвестной функции u.

Далее, заменив вспомогательную функцию u на ее выражение через х и у и, найдя интегралы, получим общее решение однородного дифференциального уравнения.

Пример. Решить уравнение .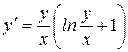

Введем вспомогательную функцию u.

.

Отметим, что введенная нами функция u всегда положительна, т.к. в противном случае теряет смысл исходное дифференциальное уравнение, содержащее .

Подставляем в исходное уравнение:

Разделяем переменные:

Интегрируя, получаем:

Переходя от вспомогательной функции обратно к функции у, получаем общее решение:

Линейные уравнения

Дифференциальное уравнение называется линейным относительно неизвестной функции и ее производной, если оно может быть записано в виде:

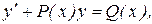(8.7)

при этом, если правая часть Q(x) равна нулю, то такое уравнение называется линейным однороднымдифференциальным уравнением, если правая часть Q(x) не равна нулю, то такое уравнение называется линейным неоднороднымдифференциальным уравнением.

P(x) и Q(x)- функции непрерывные на некотором промежутке a < x < b.

Для интегрирования линейных неоднородных уравнений (Q(x)¹0) применяются в основном два метода: метод Бернулли и метод Лагранжа.

Метод Бернулли.

Суть метода заключается в том, что искомая функция представляется в виде произведения двух функций .

При этом очевидно, что .

Подставляя в исходное уравнение, получаем:

или .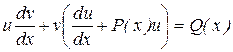

Далее следует важное замечание – т.к. первоначальная функция была представлена нами в виде произведения, то каждый из сомножителей, входящих в это произведение, может быть произвольным, выбранным по нашему усмотрению.

Выберем функцию u так, чтобы выполнялось условие .

Таким образом, можно получить функцию u, проинтегрировав, полученное дифференциальное уравнение:

Для нахождения второй неизвестной функции v подставим поученное вы-ражение для функции u в исходное уравнение 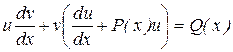с учетом того, что выражение, стоящее в скобках, равно нулю.

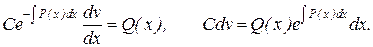
Интегрируя, можем найти функцию v:

, .

Т.е. была получена вторая составляющая произведения , которое и определяет искомую функцию.

Подставляя полученные значения, получаем:

Метод Лагранжа

Метод Лагранжа решения неоднородных линейных дифференциальных уравнений еще называют методом вариации произвольной постоянной.

Ищется решение линейного дифференциального уравнения первого порядка:

Первый шаг данного метода состоит в отбрасывании правой части уравнения и замене ее нулем.

Далее находится решение получившегося однородного дифференци-ального уравнения:

.

Для того, чтобы найти соответствующее решение неоднородного дифференциального уравнения, будем считать постоянную С₁ некоторой функцией от х.

Тогда по правилам дифференцирования произведения функций получаем: