 |
Главная |
Линейные дифференциальные уравнения второго порядка
|
из
5.00
|
Многие задачи в области механики, физики, электротехники, робото-техники, систем управления, химической технологии и других технических систем приводят клинейным дифференциальным уравнениям второго порядка.
Уравнения вида
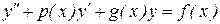 , (8.11)
, (8.11)
где 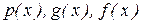 - заданные функции, называется линейным ДУ второго порядка. Это уравнение содержит неизвестную функцию
- заданные функции, называется линейным ДУ второго порядка. Это уравнение содержит неизвестную функцию 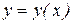 и её про-изводные
и её про-изводные 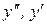 в первой степени. Функции
в первой степени. Функции 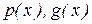 называются коэф-фициентами уравнения (8.11), а
называются коэф-фициентами уравнения (8.11), а 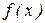 - свободным членом.
- свободным членом.
Если свободный член 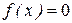 , то уравнение (8.11) называется линейным однородным, а если
, то уравнение (8.11) называется линейным однородным, а если 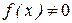 , то уравнение (8.11) неоднородно.
, то уравнение (8.11) неоднородно.
Линейные однородные ДУ второго порядка
Рассмотрим линейное однородное дифференциальное уравнение (ЛОДУ) второго порядка:
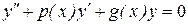 (8.12)
(8.12)
и установим некоторые свойства решений этого уравнения.
Теорема.Если функции 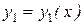 и
и 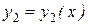 являются решениями уравнения (8.12), то решением этого уравнения является также линейная комбинация этих функций
являются решениями уравнения (8.12), то решением этого уравнения является также линейная комбинация этих функций
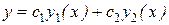 , (8.13)
, (8.13)
где с1 и с2 - произвольнее постоянные.
Доказательство. Подставим функцию (8.13) и её производные в левую часть (8.12). Получим
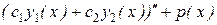 (
( 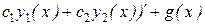 (
( 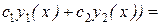
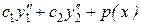
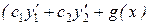 (
( 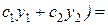
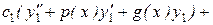
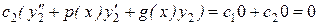 .
.
Таким образом, функция 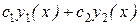 является также является ре-шением уравнения (8.12).
является также является ре-шением уравнения (8.12).
Итак, функция вида у = 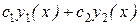 с произвольными постоянными с1 и с2 является решением уравнения (8.12). Докажем в последствии, что (8.13) при некоторых условиях является общим решением (8.12). Для этого рассмотрим понятие линейной зависимости и линейной независимости функций.
с произвольными постоянными с1 и с2 является решением уравнения (8.12). Докажем в последствии, что (8.13) при некоторых условиях является общим решением (8.12). Для этого рассмотрим понятие линейной зависимости и линейной независимости функций.
Функции 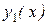 и
и 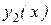 называется линейно зависимыми на (a,b), если существуют такие числа с1 и с2, из которых хотя бы одно отлично от нуля, что для любого
называется линейно зависимыми на (a,b), если существуют такие числа с1 и с2, из которых хотя бы одно отлично от нуля, что для любого 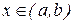 имеет место равенство
имеет место равенство
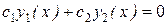 . (8.14)
. (8.14)
Очевидно, что если функции 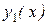 и
и 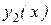 линейно зависимы, то они пропорциональны. Действительно, если
линейно зависимы, то они пропорциональны. Действительно, если 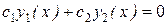 , причём
, причём 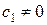
и 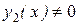 , то
, то 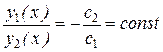 . Верно и обратное.
. Верно и обратное.
Функции 
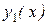 и
и 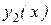 называется линейно независимыми на (a,b), если не существует таких чисел с1 и с2, из которых хотя бы одно отлично от нуля, что для любого
называется линейно независимыми на (a,b), если не существует таких чисел с1 и с2, из которых хотя бы одно отлично от нуля, что для любого 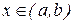 имеет место равенство (8.14).
имеет место равенство (8.14).
Другими словами, равенство (8.14) выполняется сразу для всех 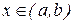 , если только с1 = с2 = 0.
, если только с1 = с2 = 0.
Очевидно, что если функции 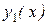 и
и 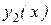 линейно независимы, то их отношение
линейно независимы, то их отношение 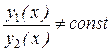 , т.е. они не пропорциональны.
, т.е. они не пропорциональны.
Так, например, функции 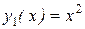 и
и 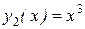 линейно независимы на любом интервале
линейно независимы на любом интервале 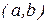 , поскольку
, поскольку 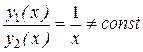 , а функции
, а функции 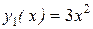 и
и 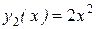 линейно зависимы на любом интервале
линейно зависимы на любом интервале 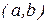 , так как
, так как 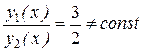 .
.
Признак линейной зависимости системы функций связан с так назы-ваемым определителем Вронского или вронскианом. Для двух дифферен-цируемых функций 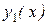 и
и 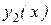 вронскиан имеет следующий вид
вронскиан имеет следующий вид
W(x) = 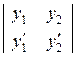 .
.
Имеют место следующие теоремы.
Теорема 1. Если дифференцируемые функции 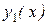 и
и 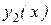 линейно зависимы на (a,b), то определитель Вронского на этом интервале равен нулю.
линейно зависимы на (a,b), то определитель Вронского на этом интервале равен нулю.
Доказательство. Так как функций 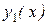 и
и 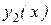 линейно зависимы, то они пропорциональны
линейно зависимы, то они пропорциональны 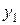 = α
= α 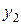 и
и 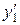 = α
= α 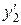 , тогда определитель Вронского
, тогда определитель Вронского
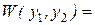
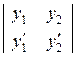 =
= 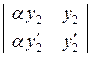 = 0.
= 0.
Теорема 2.Для того, чтобы две дифференцируемые функций 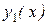 и
и 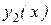 были бы линейно независимы на [a,b] необходимо и достаточно, чтобы определитель Вронского на этом сегменте был бы отличен от нуля.
были бы линейно независимы на [a,b] необходимо и достаточно, чтобы определитель Вронского на этом сегменте был бы отличен от нуля.
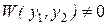 .
.
Теорема(о структуре общего решения ЛОДУ второго порядка) Если два решения 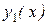 и
и 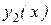 ЛОДУ
ЛОДУ 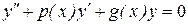 линейно независимы, то их линейная комбинация
линейно независимы, то их линейная комбинация
у = 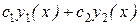

является общим решением этого уравнения.
Доказательство. Так как 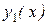 и
и 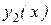 являются решениями уравнения (8.12), то их линейная комбинация у =
являются решениями уравнения (8.12), то их линейная комбинация у = 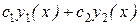 также – решение этого уравнения. Остаётся доказать, что это решение общее, т.е., что из него можно выделить единственное частное решение, удовлетворяющее заданным начальным условиям
также – решение этого уравнения. Остаётся доказать, что это решение общее, т.е., что из него можно выделить единственное частное решение, удовлетворяющее заданным начальным условиям
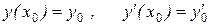 , (8.15)
, (8.15)
Подставляем данные условия в решение 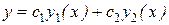 , получим систему уравнений
, получим систему уравнений
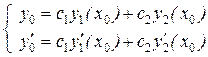 , (8.16)
, (8.16)
относительно неизвестных с1 и с2.
Определитель этой системы
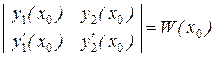
равен значению вронскиана в точке х = х0 . Но так как 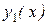 и
и 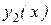 являются линейно независимыми на [a,b] , то согласно теореме 2,
являются линейно независимыми на [a,b] , то согласно теореме 2, 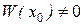 . А это означает, что система (8.16) имеет единственное решение:
. А это означает, что система (8.16) имеет единственное решение:
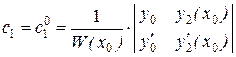 ,
, 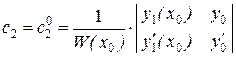 .
.
Решение 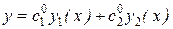 является единственным частным решением уравнения (8.12), удовлетворяющим начальным условиям (8.15). Теорема доказана.
является единственным частным решением уравнения (8.12), удовлетворяющим начальным условиям (8.15). Теорема доказана.
|
из
5.00
|
Обсуждение в статье: Линейные дифференциальные уравнения второго порядка |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

