Cм 18Дисперсия случайной величины

Дисперсия случайной величины характеризует меру разброса случайной величины около ее математического ожидания.

Если случайная величина x имеет математическое ожидание Mx , то дисперсией случайной величины x называется величина Dx = M(x - Mx )2.

Легко показать, что Dx = M(x - Mx )2= Mx 2 - M(x )2.

Эта универсальная формула одинаково хорошо применима как для дискретных случайных величин, так и для непрерывных. Величина Mx 2 >для дискретных и непрерывных случайных величин соответственно вычисляется по формулам

, .

Для определения меры разброса значений случайной величины часто используется среднеквадратичное отклонение , 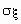связанное с дисперсией соотношением .

Основные свойства дисперсии:

дисперсия любой случайной величины неотрицательна, Dx 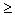0;

дисперсия константы равна нулю, Dc=0;

для произвольной константы D(cx ) = c2D(x );

дисперсия суммы двух независимых случайных величин равна сумме их дисперсий: D(x ± h ) = D(x ) + D (h ).

20Дисперсия, как характеристика разброса случайной величины, имеет один недостаток. Если, например, Х – ошибка измерения имеет размерность ММ2, то дисперсия имеет размерность . Поэтому часто предпочитают пользоваться другой характеристикой разброса – средним квадратическим отклонением, которое равно корню квадратному из дисперсии.

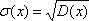
Среднее квадратическое отклонение имеет ту же размерность, что и сама случайная величина.

Кроме математического ожидания и дисперсии, для оценки случайной величины используются начальные и центральные моменты случайной величины.

Начальным моментом порядка 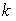случайной величины называют математическое ожидание величины :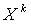

.

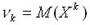
Центральным моментом порядка 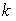случайной величины называют математическое ожидание величины :

.

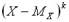
Начальный момент первого порядка равен математическому ожиданию самой случайной величины .

Центральный момент первого порядка равен нулю:

.

Централный момент второго порядка представляет собой дисперсию случайной величины

Для дискретных случайных величин:

;

Коэффицие́нт асимметри́и (skewness) — числовая характеризующая степени несимметричности распределения данной случайной величины.

Определение

Пусть задана случайная величина , такая что .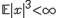

Коэффициент асимметрии распределения случайной величины определяется формулой:

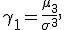
где

— третий центральный момент случайной величины ;

— стандартное отклонение случайной величины ;

— дисперсия или второй центральный момент случайной величины ;

Если плотность распределения симметрична, то .

Если левый хвост распределения тяжелее, то .

Если правый хвост распределения тяжелее, то .

Иногда вместо используется обозначение .

Эксцесс

Нормальное распределение наиболее часто используется в теории вероятностей и в математической статистике, поэтому график плотности вероятностей нормального распределения стал своего рода эталоном, с которым сравнивают другие распределения. Одним из параметров, определяющих отличие распределения случайной величины x , от нормального распределения, является эксцесс.

Эксцесс g случайной величины x определяется равенством .

У нормального распределения, естественно, g = 0. Если g (x ) > 0, то это означает, что график плотности вероятностей px (x) сильнее “заострен”, чем у нормального распределения, если же g (x ) < 0, то “заостренность” графика px (x) меньше, чем у нормального распределения.

21Математическая статистика – это наука, занимающаяся методами обработки экспериментальных данных. Любая наука решает в порядке возрастания сложности и важности следующие задачи:

1) описание явления;

2) анализ и прогноз;

3) поиск оптимального решения.

Такого рода задачи решает и математическая статистика:

1) систематизировать полученный статистический материал;

2) на основании полученных экспериментальных данных оценить интересующие нас числовые характеристики наблюдаемой случайной величины;

3) определить число опытов, достаточное для получения достоверных результатов при минимальных ошибках измерения.

Одной из задач третьего типа является задача проверки правдоподобия гипотез. Она может быть сформулирована следующим образом: имеется совокупность опытных данных, относящихся к одной или нескольким случайным величинам. Необходимо определить, противоречат ли эти данные той или иной гипотезе, например, гипотезе о том, что исследуемая случайная величина распределена по определенному закону, или две случайные величины некоррелированы (т.е. не связаны между собой) и т.д. В результате проверки правдоподобия гипотезы она либо отбрасывается, как противоречащая опытным данным, либо принимается, как приемлемая.

Таким образом, математическая статистика помогает экспериментатору лучше разобраться в полученных опытных данных, оценить, значимы или нет определенные наблюденные факты, принять или отбросить те или иные гипотезы о природе рассматриваемого явления.