Свойства ортогонального проецирования

Свойства параллельного проецирования

При параллельном проецировании сохраняются все свойства центрального проецирования, а также возникают следующие новые свойства.

1. Проекции параллельных прямых параллельны между собой, т.е., если а ½½ b, то a₁ ½½ b₁. Пусть отрезки АВ и DE параллельны (рис. 1.3), тогда проецирующие плоскости AA₁BB₁ и DD₁E₁Eбудут также параллельны. Следовательно, линии A₁B₁ и D₁E₁ пересечения этих плоскостей с П₁ будут параллельны.

2.Отношение отрезков, принадлежащих параллельным прямым или одной прямой, равно отношению проекций этих отрезков, т.е., если AB ½½ DE, то D AB / DE = D A₁B₁ / D₁E₁

3. При параллельном перемещении плоскости проекций проекция фигуры не изменяется. Если П₁П₂, то D A₁B₁C₁ = D A₂B₂C₂ (рис.1.4).

Рис.1.4 Рис.1.5

Свойства ортогонального проецирования

Наряду со свойствами параллельного (косоугольного) проецирования ортогональное проецирование имеет следующие свойства.

1. Отрезок прямой в общем случае равен гипотенузе прямоугольного треугольника, у которого один катет равен его проекции на данную плоскость проекции, а второй - разности расстоянии концов отрезка до этой плоскости (рис.1.5).

2. Любой отрезок прямой и плоская фигура, параллельные плоскости проекций, проецируются на эту плоскость без искажения (рис.1.6), например, если АВ ½½ П₁, то ½ A₁B₁ ½ = ½ AB ½ ; DABC ½½ П₁, то D A₁B₁C₁ = D ABC.

Рис.1.6 Рис.1.7

3. Проекция любой фигуры (плоской фигуры, отрезка прямой и т.д.) не может быть больше самой фигуры (как следствие п. 1 и 2).

4. Ортогональные проекции двух взаимно перпендикулярных прямых, одна из которых параллельна плоскости проекций, а другая не перпендикулярна ей, взаимно перпендикулярны, т.е., если a^ b, и a ½½ П₁, то a₁ ^ b₁ (рис.1.7).
Пусть дано a ^ b. Построим проекцию a ^ b на П₁. AA₁ ^ П₁ (как проецирующий луч), следовательно, плоскость Г (AA₁ Ç b) также перпендикулярна П₁. Прямая а перпендикулярна плоскости Г, так как она перпендикулярна двум прямым AA₁ и b, принадлежащим плоскости Г. Но a₁ ½½ a (a ½½ П₁) и, следовательно, a ^ Г, откуда A₁ перпендикулярна любой прямой плоскости Г, в том числе и b₁. Отсюда справедливо, что a₁ ^ b₁.
Это доказательство относится как к пересекающимся прямым, так и к скрещивающимся. Как видно из чертежа, если с Ì Г, а Г ^ Q , то c₁ ^a₁.

 

Ортогональное проецирование

Направление проецирования перпендикулярно (ортогонально) плоскости проекций S 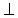π₁ (рис. 1.11). Ортогональное проецирование является частным случаем параллельного проецирования.

Ортогональное проецирование находит широкое применение в инженерной практике для изображения геометрических фигур на плоскости, т. к. обладает рядом преимуществ перед центральным и параллельным (косоугольным) проецированием к которым можно отнести:

.

Рис. 1.10. Пример инвариантного свойства 9

.

Рис. 1.11. Ортогональная проекция прямого угла

а) простоту графических построений для определения ортогональных проекций точек;

б) возможность при определенных условиях сохранить на проекциях форму и размеры проецируемой фигуры.

Указанные преимущества обеспечили широкое применение ортогонального проецирования в технике, в частности для составления машиностроительных чертежей.

Для ортогонального проецирования справедливы все девять инвариантных свойств, рассмотренных выше. Кроме того, необходимо отметить еще одно, десятое, инвариантное свойство, которое справедливо только для ортогонального проецирования.

10. Если хотя бы одна сторона прямого угла параллельна плоскости проекций, то на эту плоскость проекций прямой угол проецируется без искажения (рис. 1.11)

На рис. 1.11 показан прямой угол АВD, обе стороны которого параллельны плоскости проекций π₁. По инвариантному свойству 9 этот угол проецируется на плоскость π₁ без искажения, т. е. А₁В₁D₁=90°.

Возьмем на проецирующем луче DD₁ произвольную точку С, тогда полученный АВС будет прямым, т. к. АВ 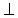ВВ₁DD₁.

Проекцией этого прямого угла АВС, у которого только одна сторона АВ параллельна плоскости проекций π₁, будет прямой угол А₁В₁D₁.

Эпюр Монжа (комплексный чертеж) или ортогональные проекции.

Суть метода ортогональных (прямоугольных) проекций состоит в том, что оригинал ортогонально проецируют на 2 или 3 взаимно-ортогональные плоскости проекций, которые затем совмещают с плоскостью чертежа.

Проецирование на три взаимно перпендикулярные плоскости проекции

 

Существует множество деталей, информацию о форме кото­рых невозможно передать двумя проекциями чертежа (рис. 75). Для того чтобы информация о сложной форме детали была представлена достаточно полно, используют проецирование на три взаимно перпендикулярные плоскости проекции: фронталь­ную — V, горизонтальную — H и профильную — W (читается «дубль вэ»). Система плоскостей проекций представляет собой трехгран­ный угол с вершиной в точке О. Пересечения плоскостей трех­гранного угла образуют прямые линии — оси проекций (OX, OY, OZ) (рис. 76). В трехгранный угол помещают предмет так, чтобы его формо­образующая грань и основание были бы параллельны соответст­венно фронтальной и горизонтальной плоскостям проекций. За­тем через все точки предмета проводят проецирующие лучи, перпендикулярные всем трем плоскостям проекций, на которых получают фронтальную, горизонтальную и профильную проекции предмета. После проецирования предмет удаляют из трехгран­ного угла, а затем горизонтальную и профильную плоскости про­екций поворачивают на 90* соответственно вокруг осей ОХ и OZ до совмещения с фронтальной плоскостью проекции и получают чертеж детали, содержащий три проекции. Рис. 75. Проецирование на две плоскости проекций не всегда дает полное представление о форме предмета Рис. 76. Проецирование на три взаимно перпендикулярные плоскости проекций   Три проекции чертежа взаимосвязаны друг с другом. Фрон­тальная и горизонтальная проекции сохраняют проекционную связь изображений, т. е. устанавливаются проекционные связи и между фронтальной и горизонтальной, фронтальной и профиль­ной, а также горизонтальной и профильной проекциями (см. рис. 76). Линии проекционной связи определяют местоположение каждой проекции на поле чертежа. Во миогнх странах мира принята другая система прямо- угольного проецирования на три взаимно перпендикулярные плоскости проекций, которая условно называется «амери­канская» (см. Приложение 3). Основное eе отличие состоит в том, что по-иному, относительно проецируемого объекта, в пространстве располагается трехгранный угол и в других направлениях разворачива­ются плоскости проекций. Поэтому горизонтальная проекция оказывается над фронтальной, а профильная проекция — справа от фронтальной. Форма большинства предметов представляет собой сочетание различных геометрических тел или их частей. Следовательно, для чтения и выполнения чертежей нужно знать, как изображаются геометрические тела в системе трех проекций на производстве (табл. 7). (Чертежи, содержащие три проекции, называются ком­плексными чертежами.) 7. Комплексные и производственные чертежи деталей простой геометрической формы

Частные положения прямой в пространстве

.

Рис. 2.1. Прямые общего положения

На рис. 2.1 показаны прямые общего положения, т. е. прямые, произвольно расположенные относительно плоскостей проекций.

Особый интерес представляют прямые частного положения, т. е. прямые, расположенные определенным образом относительно плоскостей проекций: параллельные, перпендикулярные и принадлежащие плоскостям проекций.

Рассмотрим изображение на эпюре и отметим основные свойства этих прямых.

Прямые, параллельные плоскостям проекций.

1. Горизонтальная прямая h (рис. 2.2) – горизонталь

Горизонтальная прямая – это прямая, параллельная горизонтальной плоскости проекций π₁.

Так как все точки этой прямой равноудалены от плоскости проекций π₁ (координаты Z всех точек прямой одинаковы), то фронтальная и профильная проекции прямой соответственно параллельны координатным осям Х и Y. На плоскость проекций π₁ проецируются без искажения отрезок прямой АВ (А₁В₁=АВ) и углы наклона прямой к плоскостям проекций π₂ и π₃ (углы β⁰ и γ⁰).

2. Фронтальная прямая f (рис. 2.3) – фронталь

Фронтальная прямая – это прямая параллельная фронтальной плоскости проекций π₂. Так как все точки этой прямой равноудалены от плоскости проекций π₂ (координаты Y всех точек прямой одинаковы), то горизонтальная и профильная проекции прямой соответственно параллельны координатным осям Х и Z. На плоскость проекций π₂ проецируются без искажений отрезок этой прямой CD (C₂D₂+CD) и углы наклона прямой к плоскостям проекций π₁ и π₃ (углы α ⁰ и γ ⁰)

.

Рис. 2.2. Горизонтальная прямая

3. Профильная прямая p (рис. 2.4)

Профильная прямая – это прямая, параллельная профильной плоскости проекций π₃ . Так как все точки этой прямой равноудалены от плоскости проекций π₃ (координаты Х всех точек прямой одинаковы), то горизонтальная и фронтальная проекции прямой соответственно параллельны координатным осям Y и Z. На плоскость проекций π₃ проецируется без искажения отрезок этой прямой EF (E₃F₃=EF)и углы наклона прямой к плоскостям проекций π₁ и π₂ (углы α ⁰ и β ⁰).

Прямые, принадлежащие плоскостям проекций

Прямые, принадлежащие плоскостям проекций, являются частным случаем горизонтальных, фронтальных и профильных прямых. Характерным признаком для эпюра, на котором изображена подобная прямая будет принадлежность одной из проекций прямой соответствующей оси.

.

Рис. 2.3. Фронтальная прямая

.

Рис. 2.4. Профильная прямая

На рис. 2.5, 2.6, 2.7 показаны прямые, принадлежащие соответственно горизонтальной плоскости проекций (частный случай горизонтальной прямой Z=0), фронтальной плоскости проекций (частный случай фронтальной прямой Y=0) и профильной плоскости проекций (частный случай профильной прямой Х=0).

.

Рис. 2.5. Прямая, принадлежащая горизонтальной плоскости проекций

.

Рис. 2.6. Прямая, принадлежащая фронтальной плоскости проекций

.

Рис. 2.7. Прямая, принадлежащая профильной плоскости проекций

Прямые, перпендикулярные плоскостям проекций.

Проецирующие прямые

На рис. 2.8 и 2.9 показаны прямые, перпендикулярные соответственно горизонтальной и фронтальной плоскостям проекций

Прямая перпендикулярная горизонтальной плоскости проекций – горизонтально-проецирующая прямая. Такая прямая проецируется на плоскость π₁ в точку; ее фронтальная проекция перпендикулярна оси Х (рис. 2.8).

Прямая, перпендикулярная фронтальной плоскости проекций – фронтально-проецирующая прямая. Эта прямая проецируется на плоскость π₂ в точку, а ее горизонтальная проекция перпендикулярна оси Х (рис. 2.9).

Прямая, перпендикулярная профильной плоскости проекций – профильно-проецирующая прямая. Эта прямая проецируется на плоскость π₃ в точку, а ее фронтальная проекция перпендикулярна оси Z.

Эти прямые являются частными случаями фронтали и горизонтали.

.

Рис. 2.8. Прямая, перпендикулярная горизонтальной плоскости проекций

.

Рис. 2.9. Прямая, перпендикулярная фронтальной плоскости проекций

.

Рис. 2.10. Прямая, перпендикулярная профильной плоскости проекций

 

Способ прямоугольного треугольника

Способ прямоугольного треугольника применяется в задачах, в которых требуется определить натуральную величину отрезка, разность координат концов отрезка, углы наклона его к плоскостям проекций и так далее. Посмотрим на способ прямоугольного треугольника как частный случай замены плоскостей проекций. Это тот случай определения длины отрезка, когда один из его концов принадлежит плоскости проекций, а новая плоскость проекций проводится через сам отрезок (Рис.58). На чертеже это новая ось, совпадающая с проекцией отрезка. При этом искомая величина отрезка окажется равной гипотенузе прямоугольного треугольника, один из катетов которого есть проекция отрезка. Помимо длины треугольник содержит в себе и другие сведения об отрезке.

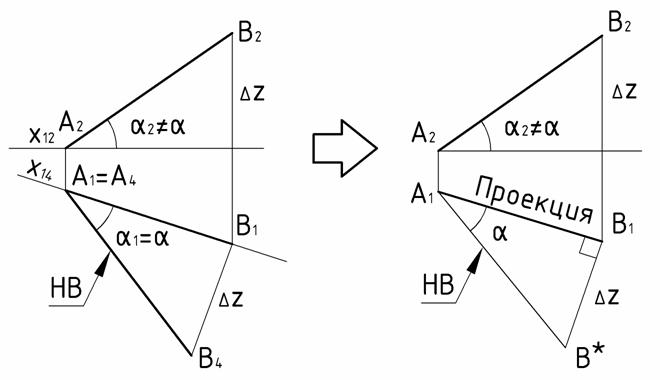
Точно такой же треугольник с точно такими же сведениями об отрезке можно получить без операции проецирования и даже – на безосном комплексном чертеже. Применим одну из проекций отрезка за катет прямоугольного треугольника. Второй катет равен разности координат концов отрезка в направлении, в каком была задана выбранная проекция. Что имеем в итоге:

1) Длина отрезка равна гипотенузе прямоугольного треугольника, один катет которого – это проекция отрезка, второй катет – равен разности координат концов отрезка, измеренной в направлении получения использованной проекции отрезка.

2) Угол наклона отрезка к плоскости проекций равен углу между гипотенузой и проекцией отрезка на той же плоскости.

Пример (Рис.59). Определить длину отрезка и угол его наклона к плоскости .

При определении длины отрезка за катет прямоугольного треугольника может быть выбрана любая проекция отрезка. Другое дело, если определяется угол наклона отрезка к той или иной плоскости проекций. Здесь выбор падает на проекцию отрезка, принадлежащую именно той же плоскости проекций.

Решение:

Строим прямоугольный треугольник, приняв за катет фронтальную проекцию отрезка . Второй катет по длине равен разности координат точек и в направлении мнимой в данном случае оси y. На чертеже эта разница берется на другой плоскости проекций: на плоскости . Из построенного треугольника делаем выводы:

1) ,

 

 

Точка на прямой.

Комплексный чертеж точки, находящейся на прямой. Точку на прямой можно рассматривать как одну из точек, принадлежащих этой прямой. Пусть дан отрезок АВ и его проекции А₁В₁ и А₂В₂. На отрезке АВ лежит точка С, требуется определить ее проекции. Так как точка принадлежит отрезку, то ее проекции будут лежать на одноименных проекциях отрезка (фиг.211,а).

Проведем через точку С проектирующие прямые, получим горизонтальную проекцию С₁ точки С на горизонтальной проекции А₁В₁ отрезка АВ и фронтальную проекцию С₂ на фронтальной проекции А₂В₂ (фиг.211,б). Рассматривая комплексный чертеж точки С, замечаем, что обе проекции С₁и С₂ лежат на одной вертикальной линии связи, как проекции одной и той же точки. Если одна (фиг.211,в) или две проекции (фиг.211,г) точки не лежат на одноименных проекциях отрезка, то точка не лежит на отрезке.
Следовательно, для того чтобы точка лежала на прямой, необходимо, чтобы проекции этой точки не только лежали на одноименных проекциях прямой, но и находились на одной линии связи.
Это правило имеет исключение в том случае, когда точка лежит на горизонтальной прямой, данной фронтальной и профильной проекциями, на фронтальной прямой, данной горизонтальной и профильной проекциями, или профильной прямой, данной горизонтальной и фронтальной проекциями.

Тогда, для того чтобы определить, лежит ли точка на прямой, необходимо построить третью проекцию. На (фиг.212) видно, что точка Е не лежит на отрезке АВ, так как профильная проекция Е₃ точки Е не лежит на профильной проекции А₃В₃ отрезка АВ; точка F лежит на отрезке АВ, так как не только ее горизонтальная F₁ фронтальная F₂, но и профильная F₃проекции лежат на одноименных проекциях отрезка АВ.

 

Взаимное расположение двух прямых в пространстве

Взаимное расположение двух прямых и пространстве характеризуется следующими тремя возможностями. 1. Прямые лежат в одной плоскости и не имеют общих точек — параллельные прямые. 2. Прямые лежат и одной плоскости и имеют одну общую точку — прямые пересекаются. 3. В пространстве две прямые могут быть расположены еще так, что не лежат ни в одной плоскости. Такие прямые называются скрещивающимися (не пересекаются и не параллельны). Теорема. Если одна из двух прямых лежит в некоторой плоскости, а другая пересекает эту плоскость и точке, которая не лежит на первой прямой, то эти прямые скрещиваются. На рис. 26 прямая a лежит в плоскости , а прямая с пересекает в точке N. Прямые a и с — скрещивающиеся. Теорема. Через каждую из двух скрещивающихся прямых проходит только одна плоскость, параллельная другой прямой. На рис. 26 прямые a и b скрещиваются. Черен прямую а проведена плоскость || b (в плоскости указана прямая a1 || b). Примеры скрещивающихся прямых: трамвайный рельс и троллейбусный провод по пересекающейся улице, нeпересекающиеся и непараллельные ребра пирамид или призм и пр. Все три случая можно видеть еще на примере прямых, по которым встречаются стены и потолок или стены и пол комнаты.

 

 

ПЛОСКОСТЬ

Плоскость – одно из основных понятий геометрии. При систематическом изложении геометрии понятие плоскость обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии. Некоторые характеристические свойства плоскости:

1. Плоскость есть поверхность, содержащая полностью каждую прямую, соединяющую любые ее точки;

2. Плоскость есть множество точек, равноотстоящих от двух заданных точек.

Плоскость в линейной алгебре - поверхность первого порядка: в декартовой системе координат плоскость может быть задана уравнением 1-ой степени. Общее уравнение плоскости:

Ax+By+Cz+D=0,

где А, В, С, и D - постоянные, причем А, В и С одновременно не равны нулю.

 

СПОСОБЫ ГРАФИЧЕСКОГО ЗАДАНИЯ ПЛОСКОСТЕЙ

Положение плоскости в пространстве можно определить:

 

Двумя параллельными прямыми

а) модель	б) эпюр
Рисунок 5.4. Плоскость заданная двумя параллельными прямыми линиями

До сих пор мы рассматривали ортогональные проекции точки на комплексном чертеже. Теперь рассмотрим комплексный чертёж линии. Комплексный чертёж линии представляет собой совокупность проекций точек этой линии на две или три плоскости проекций Выполнении графических работ Виды проецирования, типы задач , графические задания Сборочный чертеж

 

Плоскости уровня.

1. Плоскость λ параллельна плоскости П₁. Такую плоскость называют горизонтальной. Фронтальная и профильная проекции параллельны осям х иу (фиг.225,а).

2. Плоскость μ параллельна плоскости П₂. Такую плоскость называют фронтальной. Горизонтальная и профильная проекции параллельны осям х иz (фиг.225,б).
3. Плоскость θ параллельна плоскости П₃. Такую плоскость называют профильной. Фронтальная и горизонтальная проекции параллельны осям z иу (фиг.225,в).
Плоскости уровня называют также дважды проектирующими.
Плоскости уровня принято изображать их проекциями.
Особенность этих плоскостей состоит в том, что прямая, кривая или фигура, лежащие в этих плоскостях, проектируются на параллельную ей плоскость проекций в натуральную величину, а на две другие - отрезками, сливающимися с соответствующими проекциями плоскости.
Например: отрезок АВ расположен в горизонтальной плоскости λ; в этом случае его горизонтальная проекция равна натуральной величине отрезка (фиг.226,а).