 |
Главная |
Установление математической формы связи между изучаемыми признаками
|
из
5.00
|
Целью данного этапа является нахождение конкретного математического выражения функции:
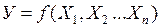 .
.
В данном случае наиболее сложной проблемой является выбор формы связи (типа аналитического уравнения – прямолинейная зависимость, криволинейная зависимость и т.д.) выбор типа функции должен опираться на теоретические исследования или же находиться путем последовательного подбора различных типов уравнений.
При выборе уравнений можно использовать некоторые общие приемы: графический анализ, с целью выявления характера зависимости между зависимыми парами переменных; выбор простейших видов функций, а при выявлении их непригодности переход к более сложным уравнениям; выявление наиболее пригодного типа функции путем сравнения оценок тесноты связи и статистической надежности как уравнения в целом так и его отдельных параметров (коэффициентов регрессии).
При парных корреляционных связях наиболее часто используют следующие типы функций:
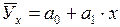 - уравнение прямой,
- уравнение прямой,
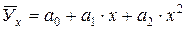 - уравнение параболы второго порядка,
- уравнение параболы второго порядка,
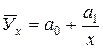 - уравнение гиперболы,
- уравнение гиперболы,
 - уравнение показателей кривой – экспоненты.
- уравнение показателей кривой – экспоненты.
Для аппроксимации фактических данных используют полиномы П.Л. Чебышева:  .
.
Повышение порядка полинома производят до тех пор, пока остаточная дисперсия продолжает уменьшаться. Если при переходе к уравнению регрессии более высокого порядка остаточная дисперсия уменьшается незначительно, то аппроксимацию считают достаточной.
Учитывая, что на практике путем математических преобразований многие функции можно привести к линейному виду, рекомендуется построение уравнений множественной регрессии в линейной форме
 .
.
Сформированная статистическая совокупность и подобранная форма уравнения позволяют перейти к расчету параметров модели. Для расчетов параметров разработаны различные методы, однако практически чаще всего используют метод наименьших квадратов. Суть его в том, чтобы сумма квадратов отклонений фактических данных от исчисленных по выбранному уравнению была наименьшей.
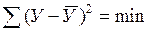 .
.
При использовании метода наименьших квадратов получают системы «нормальных» уравнений. Например, при использовании в качестве формы связи уравнения прямой после необходимых преобразований получают следующую систему «нормальных» уравнений
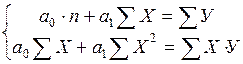 .
.
Для множественной корреляционной зависимости при n-ом количестве факторов ( 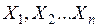 ) для определения параметров уравнения регрессии также необходимо составить систему «нормальных» уравнений, которая содержит (
) для определения параметров уравнения регрессии также необходимо составить систему «нормальных» уравнений, которая содержит ( 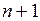 ) линейное уравнение с (
) линейное уравнение с ( 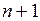 ) неизвестными параметрами
) неизвестными параметрами
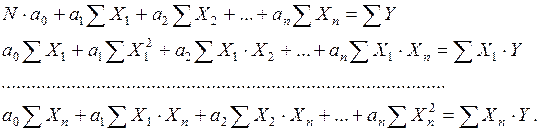
Решение системы «нормальных» уравнений при значительном количестве параметров функции представляет некоторые трудности в вычислении. Поэтому, расчеты параметров уравнений модели корреляционной зависимости и других характеристик модели целесообразно производить с использованием ЭВМ.
|
из
5.00
|
Обсуждение в статье: Установление математической формы связи между изучаемыми признаками |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

