 |
Главная |
Разложение булевой функции по одной и нескольким переменным. Совершенная конъюктивная нормальная форма
|
из
5.00
|
Совершеннойконъюнктивной нормальной формой(СКНФ) формулы  называется такая КНФ, для которой выполняются следующие условия:
называется такая КНФ, для которой выполняются следующие условия:
1. Все элементарные дизъюнкции, входящие в КНФ  , различны.
, различны.
2. Все элементарные дизъюнкции, входящие в КНФ  , содержат литеры, соответствующие всем переменным.
, содержат литеры, соответствующие всем переменным.
3. Каждая элементарная дизъюнкция, входящая в КНФ  , не содержит двух одинаковых литер.
, не содержит двух одинаковых литер.
4. Каждая элементарная дизъюнкция, входящая в КНФ  , не содержит переменную и ее отрицание.
, не содержит переменную и ее отрицание.
СКНФ  можно получить двумя способами:
можно получить двумя способами:
1. по таблице истинности;
2. с помощью равносильных преобразований.
По первому способу по таблице истинности получаем СДНФ  , а СКНФ
, а СКНФ  можно получить, следуя следующему правилу
можно получить, следуя следующему правилу

С помощью равносильных преобразований формулы  получают КНФ
получают КНФ  . При этом в полученной КНФ возможны следующие ситуации:
. При этом в полученной КНФ возможны следующие ситуации:
1. Элементарная дизъюнкция  КНФ
КНФ  не содержит переменную
не содержит переменную  , тогда используются следующие равносильные преобразования:
, тогда используются следующие равносильные преобразования:

2. Если в КНФ  входят две одинаковые элементарные дизъюнкции, то используя следующее равносильное преобразование:
входят две одинаковые элементарные дизъюнкции, то используя следующее равносильное преобразование:
 ,
,
одну элементарную дизъюнкцию можно отбросить.
3. Если элементарная дизъюнкция  КНФ
КНФ  содержит одновременно переменную
содержит одновременно переменную  и ее отрицание, то используя следующие равносильные преобразования:
и ее отрицание, то используя следующие равносильные преобразования:
 ,
,
эту элементарную дизъюнкцию можно отбросить.
4. Если элементарная дизъюнкция  КНФ
КНФ  содержит дважды переменную
содержит дважды переменную  , то используя следующее равносильное преобразование:
, то используя следующее равносильное преобразование:
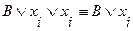 ,
,
одну переменную  можно отбросить.
можно отбросить.
СКНФ формулы  существует в единственном виде.
существует в единственном виде.
ПРИМЕР
Получить СКНФ формулы 
С помощью равносильных преобразований получаем СКНФ  :
:

С помощью таблицы истинности получаем СДНФ  :
:

| 
| 
| 
| 
| 
| 
|
СДНФ 

Очевидно, что в результат двух способов совпадает.
СДНФ формулы  можно получить из СКНФ
можно получить из СКНФ  , используя следующее правило:
, используя следующее правило:

Билет №7
Теорема Поста
Функциональный набор логических функций - это такой набор функций, который позволяет любую функцию математической логики описать с помощью функций данного набора.
Теорема Поста. Для того чтобы набор функций {f1,f2,……fn} был функционально полный необходимо и достаточно, чтобы для всего набора функций в целом не выполнялись свойства сохранения нуля, сохранения единицы, линейности, монотонности и самодвойственности.
Полноту набора удобно определять по таблице Поста, в клетках которой ставится знак «+» или «-» в зависимости от того, обладает функция из этого набора тем или иным свойством. В силу теоремы Поста для полноты системы необходимо и достаточно, чтобы в каждом столбце был хотя бы один минус.
| { } | T0 | T1 | L | M | S |
| F1 | + | + | + | + | - |
| F2 | - | - | - | - | + |
ПРИМЕР
Доказать, что набор функций6 дизъюнкция и отрицание является функционально полным.
| T0 | T1 | L | M | S | |

| - | - | + | - | + |
| V | + | + | - | + | - |
Теорема Поста о полноте
Для того чтобы система функций была полной, необходимо и достаточно, чтобы она не содержалась целиком ни в одном из классов T0, T1, L, S, M.
Доказательство. Докажем необходимость этого условия. Пусть система
N = {f1, f2, ...fs, ...} полна в Р2, покажем, что тогда она не лежит целиком в Q, где через Q обозначим любой из классов T0, T1, L, S, M. Докажем от противного, пусть N ??Q, очевидно, [N] ??[Q] = Q, но [N] = P2, т.к. N – полна в Р2, отсюда Р2=Q, но это не так. Необходимость доказана.
Докажем достаточность. Пусть F = {f0, f1, fL, fm, fs}, где f0?T0, f1?T1, fL?L, fs?S и fm?M. Покажем, что суперпозицией функций системы F можно получить полную систему G = {x1&x2, }.
1. Пусть g(x) = f0(x, …, x). Тогда g(0) = f( 0, …, 0) = 1. Далее возможны два случая:
g(1) = 1. Тогда g(x) ? 1. Функция h(x) = f1(g(x), …, g(x)) = f1(1, …, 1) = 0, т.е. h(x) ? 0. Получили константы 0 и 1;
g(1) = 0. Тогда g(x) = . По лемме о несамодвойственной функции суперпозицией над {fs, } можно получить одну из констант, например, 0. Тогда f0(0, …, 0) = 1 есть другая константа.
В обоих случаях получили обе константы.
2. По лемме о немонотонной функции суперпозицией над {fm, 0, 1} можно получить отрицание.
3. По лемме о нелинейной функции суперпозицией над {fL, 1, } можно получить конъюнкцию. Теорема доказана.
Следствие. Всякий замкнутый класс функций из Р2, не совпадающий с Р2 содержится, по крайней мере, в одном из замкнутых классов T0, T1, L, S, M. Действительно, если N не является подмножеством Q, то [N] = P2, что неверно.
Билет №8
|
из
5.00
|
Обсуждение в статье: Разложение булевой функции по одной и нескольким переменным. Совершенная конъюктивная нормальная форма |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

