Уравнения с разделяющимися переменными

Определение. Дифференциальное уравнение 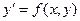называется уравнением с разделяющимися переменными, если его можно записать в виде

.

Такое уравнение можно представить также в виде:

Перейдем к новым обозначениям

Получаем:

После нахождения соответствующих интегралов получается общее решение дифференциального уравнения с разделяющимися переменными.

Если заданы начальные условия, то при их подстановке в общее решение находится постоянная величина С, а, соответственно, и частное решение.

Однородные уравнения.

Определение. Функция f(x, y) называется однородной n – го измерения относительно своих аргументов х и у, если для любого значения параметра t (кроме нуля) выполняется тождество:

Определение. Дифференциальное уравнение вида 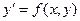называется однородным, если его правая часть f(x, y) есть однородная функция нулевого измерения относительно своих аргументов.

Любое уравнение вида 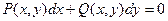является однородным, если функции P(x, y) и Q(x, y) – однородные функции одинакового измерения.

Решение любого однородного уравнения основано на приведении этого уравнения к уравнению с разделяющимися переменными.

Рассмотрим однородное уравнение

Т.к. функция f(x, y) – однородная нулевого измерения, то можно записать:

Т.к. параметр t вообще говоря произвольный, предположим, что . Получаем:

Правая часть полученного равенства зависит фактически только от одного аргумента , т.е.

Исходное дифференциальное уравнение таким образом можно записать в виде:

Далее заменяем y = ux, .

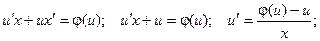
таким образом, получили уравнение с разделяющимися переменными относительно неизвестной функции u.

Далее, заменив вспомогательную функцию u на ее выражение через х и у и найдя интегралы, получим общее решение однородного дифференциального уравнения.

Уравнения, приводящиеся к однородным.

Кроме уравнений, описанных выше, существует класс уравнений, которые с помощью определенных подстановок могут приведены к однородным.

Это уравнения вида .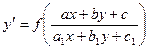

Если определитель 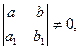то переменные могут быть разделены подстановкой

где a и b - решения системы уравнений

Линейные уравнения.

Определение. Дифференциальное уравнение называется линейным относительно неизвестной функции и ее производной, если оно может быть записано в виде:

при этом, если правая часть Q(x) равна нулю, то такое уравнение называется линейным однороднымдифференциальным уравнением, если правая часть Q(x) не равна нулю, то такое уравнение называется линейным неоднороднымдифференциальным уравнением.

P(x) и Q(x)- функции непрерывные на некотором промежутке a < x < b.

25.Дифференциальные уравнения высших порядков. Теорема Коши существования и единственности решения. Задача Коши.
Дифференциальным уравнением порядка n называется уравнение вида:

В некоторых случаях это уравнение можно разрешить относительно y⁽ⁿ⁾:

Так же как и уравнение первого порядка, уравнения высших порядков имеют бесконечное количество решений.

Определение. Решение 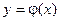удовлетворяет начальным условиям , если

Определение. Нахождение решения уравнения , удовлетворяющего начальным условиям , называется решением задачи Коши.

Теорема Коши. (Теорема о необходимых и достаточных условиях существования решения задачи Коши).

Если функция (n-1) –й переменных вида в некоторой области D (n-1)- мерного пространства непрерывна и имеет непрерывные частные производные по , то какова бы не была точка ( ) в этой области, существует единственное решение 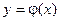уравнения , определенного в некотором интервале, содержащем точку х₀, удовлетворяющее начальным условиям .

Дифференциальные уравнения высших порядков, решение которых может быть найдено аналитически, можно разделить на несколько основных типов.

Рассмотрим подробнее методы нахождения решений этих уравнений.

26.Дифференциальные уравнения, допускающие понижения порядка.
Уравнения, допускающие понижение порядка.

Понижение порядка дифференциального уравнения – основной метод решения уравнений высших порядков. Этот метод дает возможность сравнительно легко находить решение, однако, он применим далеко не ко всем уравнениям. Рассмотрим случаи, когда возможно понижение порядка.

27Линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами.
Линейные дифференциальные уравнения высших порядков.

Определение. Линейным дифференциальным уравнением n – го порядка называется любое уравнение первой степени относительно функции у и ее производных вида:

где p₀, p₁, …,p_n – функции от х или постоянные величины, причем p₀ ¹ 0.

Левую часть этого уравнения обозначим L(y).

Определение. Если f(x) = 0, то уравнение L(y) = 0 называется линейным однороднымуравнением, если f(x) ¹ 0, то уравнение L(y) = f(x) называется линейным неоднородным уравнением, если все коэффициенты p₀, p₁, p₂, … p_n – постоянные числа, то уравнение L(y) = f(x) называется линейным дифференциальным уравнением высшего порядка с постоянными коэффициентами.

Отметим одно важное свойство линейных уравнений высших порядков, которое отличает их от нелинейных. Для нелинейных уравнений частный интеграл находится из общего, а для линейных – наоборот, общий интеграл составляется из частных. Линейные уравнения представляют собой наиболее изученный класс дифференциальных уравнений высших порядков. Это объясняется сравнительной простотой нахождения решения. Если при решении каких – либо практических задач требуется решить нелинейное дифференциальное уравнение, то часто применяются приближенные методы, позволяющие заменить такое уравнение “близким” к нему линейным.

Рассмотрим способы интегрирования некоторых типов линейных дифференциальных уравнений высших порядков.