 |
Главная |
Знакопеременные ряды. Абсолютная и условная сходимость
|
из
5.00
|
Пусть 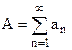 и ряд
и ряд 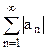 сходятся одновременно, то А также и при этом говорят, что ряд A сходится абсолютно.
сходятся одновременно, то А также и при этом говорят, что ряд A сходится абсолютно.
Если  сходится,
сходится, 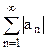 – расходится, то А сходится условно
– расходится, то А сходится условно
Абсолютная и условная сходимость рядов.
Рассмотрим некоторый знакопеременный ряд (с членами произвольных знаков).
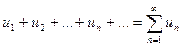 (1)
(1)
и ряд, составленный из абсолютных величин членов ряда (1):
 (2)
(2)
Теорема. Из сходимости ряда (2) следует сходимость ряда (1).
Доказательство. Ряд (2) является рядом с неотрицательными членами. Если ряд (2) сходится, то по критерию Коши для любого e>0 существует число N, такое, что при n>N и любом целом p>0 верно неравенство:

По свойству абсолютных величин:


То есть по критерию Коши из сходимости ряда (2) следует сходимость ряда (1).
Определение. Ряд 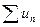 называется абсолютно сходящимся, если сходится ряд
называется абсолютно сходящимся, если сходится ряд 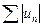 .
.
Очевидно, что для знакопостоянных рядов понятия сходимости и абсолютной сходимости совпадают.
Определение. Ряд 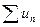 называется условно сходящимся, если он сходится, а ряд
называется условно сходящимся, если он сходится, а ряд 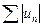 расходится.
расходится.
Признаки Даламбера и Коши для знакопеременных рядов.
Пусть 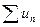 - знакопеременный ряд.
- знакопеременный ряд.
Признак Даламбера. Если существует предел  , то при r<1 ряд
, то при r<1 ряд 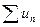 будет абсолютно сходящимся, а при r>1 ряд будет расходящимся. При r=1 признак не дает ответа о сходимости ряда.
будет абсолютно сходящимся, а при r>1 ряд будет расходящимся. При r=1 признак не дает ответа о сходимости ряда.
Признак Коши. Если существует предел  , то при r<1 ряд
, то при r<1 ряд 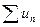 будет абсолютно сходящимся, а при r>1 ряд будет расходящимся. При r=1 признак не дает ответа о сходимости ряда.
будет абсолютно сходящимся, а при r>1 ряд будет расходящимся. При r=1 признак не дает ответа о сходимости ряда.
Свойства абсолютно сходящихся рядов.
1) Теорема. Для абсолютной сходимости ряда 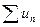 необходимо и достаточно, чтобы его можно было представить в виде разности двух сходящихся рядов с неотрицательными членами.
необходимо и достаточно, чтобы его можно было представить в виде разности двух сходящихся рядов с неотрицательными членами.
Следствие. Условно сходящийся ряд является разностью двух расходящихся рядов с неотрицательными стремящимися к нулю членами.
2) В сходящемся ряде любая группировка членов ряда, не изменяющая их порядка, сохраняет сходимость и величину ряда.
3) Если ряд сходится абсолютно, то ряд, полученный из него любой перестановкой членов, также абсолютно сходится и имеет ту же сумму.
Перестановкой членов условно сходящегося ряда можно получить условно сходящийся ряд, имеющий любую наперед заданную сумму, и даже расходящийся ряд.
4) Теорема. При любой группировке членов абсолютно сходящегося ряда (при этом число групп может быть как конечным, так и бесконечным и число членов в группе может быть как конечным, так и бесконечным) получается сходящийся ряд, сумма которого равна сумме исходного ряда.
5) Если ряды  и
и  сходятся абсолютно и их суммы равны соответственно S и s, то ряд, составленный из всех произведений вида
сходятся абсолютно и их суммы равны соответственно S и s, то ряд, составленный из всех произведений вида 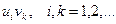 взятых в каком угодно порядке, также сходится абсолютно и его сумма равна S×s - произведению сумм перемножаемых рядов.
взятых в каком угодно порядке, также сходится абсолютно и его сумма равна S×s - произведению сумм перемножаемых рядов.
Если же производить перемножение условно сходящихся рядов, то в результате можно получить расходящийся ряд.
|
из
5.00
|
Обсуждение в статье: Знакопеременные ряды. Абсолютная и условная сходимость |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

