Корреляционные функции и спектральные плотности

Корреляционная функция — функция времени или пространственных координат, которая задает корреляцию в системах со случайными процессами.

Зависящая от времени корреляция двух случайных функций X(t) и Y(t) определяется как:

,

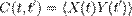где угловые скобки обозначают процедуру усреднения.

Если корреляционная функция вычисляется для одного и того же процесса, она называется автокорреляционной:

.

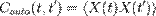Аналогично можно вычислить корреляционную функцию для процессов, происходящих в разных точках пространства в различные моменты времени:

.

Корреляционные функции широко используются в статистической физике и других дисциплинах, изучающих случайные (стохастические) процессы.

Спектральная плотность случайного процесса характеризует распределение дисперсий по частотам спектра с выделением превалирующих частот. [1]По формулам, связывающимспектральные плотности случайных процессов на входе и выходе линейной системы с ее частотной характеристикой, подсчитываем спектральные плотности каждой из составляющих ошибки. [2]В общем случае восстановитьспектральную плотность случайного процесса с непрерывными значениями параметра t по известной спектральной плотности соответствующего ему дискретного процесса, как видно из рис. 217, в, невозможно. [3]В общем случае восстановитьспектральную плотность случайного процесса, с непрерывными значениями параметра t по известной спектральной плотности соответствующего ему дискретного процесса, как видно из рис. 217, в, невозможно. [4]Описание математической модели закончим рассмотрениемспектральной плотности случайного процесса Y ( t), реализации которого получают из опыта. [5]Полученные в § 8.8 выраженияспектральной плотности выходного случайного процесса могут быть использованы для определения среднеквадратичного значения выходной величины. [6]Прежде чем подойти к понятию оспектральной плотности случайного процесса и его связи с корреляционной функцией, напомним некоторые сведения из теории интеграла Фурье. [7]Полное экспериментальное определение корреляционной функции илиспектральной плотности пространственно-временного случайного процесса связано, как правило, со значительными трудностями. Поэтому для приближенных оценок обычно используют простейшие аналитические зависимости. [8]О характере автокорреляционных функций и функцийспектральной плотности случайного процесса изменения аксиальной скорости газа wz ( t) можно судить по рис. 3.19, на котором представлены эти характеристики для слоя частиц силикагеля d 3 6 мм в колонке диаметром 220 мм и Г 0 3 при трех различных режимах псевдоожижения. [9]