 |
Главная |
Линейные однородные дифференциальные уравнения n-го порядка с постоянными коэффициентами. Вид частных решений, характеристическое уравнение
|
из
5.00
|
ЛОДУ с постоянными коэффициентами
у(n) + P1y(n-1) +…+ Pn-1 y’ + Pn y = 0, где все Pi (i=  )= const
)= const
будем искать частное решение y=ekx , к – неизвестная постоянная
y’=kekx
y’’=k2ekx
……
y(n)=k(n) ekx
k(n) ekx + P1k(n-1) ekx + … + Pnekx = ekx(k(n) + P1k(n-1) + … + Pn) = 0
ekx  0 => k(n) + P1k(n-1) + … + Pn = 0, (1)
0 => k(n) + P1k(n-1) + … + Pn = 0, (1)
ð y=ekx - решение ДУ
(1) – характеристическое уравнение для ЛОДу с постоянными коэффициентами, выражения слева характеристический многочлен.
Решением характеристич уравнения (1) дает систему частных решений ЛОДу, структура ФСР зависит от вида корней характер уравнения.
(1) – алгебраическое уравнение n-ой степени, может иметь не более, чем n корней, обознач-м эти корни характеристического уравнения через k1 ,k2 …kn
Возможны случай
1)все корни хар-го уранения вещественны и различны
2)все корни различны, но среди них есть комплексные
3)среди действительных корней имеются кратные
4)среди комплексных корней есть кратные
Общий алгоритм решения ЛОДу с постоянным коэффициентом
1) составим характер уравнение : y=ekx , k(n) + P1k(n-1) + … + Pn = 0
2) найти корни характер уравнения k1 ,k2 …kn
3) по характеру корней находим частное линейно-независимое решение по таблице 1
4) подставляем частное решение  на основе Теоремы о структуре общего решения ЛОДУ и получаем общее решение y =
на основе Теоремы о структуре общего решения ЛОДУ и получаем общее решение y = 
| № | Вид корня | Соответственное решение |
| Действ корень кратности 1 | ekx | |
Пара корней a 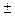 bi;кратнос 1 bi;кратнос 1
| eаxcosbx , eаxsinbx | |
| Действит корень кратност α | ekx, хekx, х2ekx, х3ekx,…, хα-1ekx | |
Пара сопряж корней α a 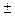 bi bi
| eаxcosbx , eаxsinbx хeаxcosbx , хeаxsinbx х2eаxcosbx , х2eаxsinbx хα-1eаxcosbx , хα-1eаxsinbx |
55. Линейные неоднородные дифференциальные уравнения n-го порядка. Теорема о структуре общего решения (док. для n=2). Теорема о суперпозиции решений (док. для n=2).
ЛНДУ
у(n) + P1y(n-1) +…+ Pn-1 y’ + Pn y = f(x) (1) Pi – непрерывна на отрезке (a,b)
Теорема о структуре общего решения ЛНДУ
Общее решение ЛНДУ есть сумма частного решения и общего решения соответственного ему однородного уравнения
Док-во:
Для уравнения 2-го порядка ( но теорема применима для уравнений любого порядка)
n=2
(1’) y” + P1(x) y’ + P2(x) y = f(x)
Обозначим у*(х) – частное решение ЛНДУ
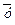 (х) – общее решение ЛОДУ
(х) – общее решение ЛОДУ
Показать, что
(2) у= у*+ 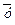 - общее решение ЛНДУ
- общее решение ЛНДУ
Найдем:
Дважды дифференцируем функцию (2) и подставляем у, y’,y” в (1’)
у*”(x) + 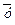 ”(x) + P1(x)[ у*(x)+
”(x) + P1(x)[ у*(x)+ 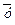 ’(x)] + P2(x)[ у*(x)+
’(x)] + P2(x)[ у*(x)+ 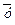 (x)] =
(x)] =
= [у*”(x)+ P1(x) у*’(x)+ P2(x) у*(x)] + [ 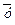 ”(x) + P1(x)
”(x) + P1(x) 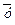 ’ (x)+ P2(x)
’ (x)+ P2(x) 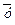 (x)] = f(x) + 0 = 0
(x)] = f(x) + 0 = 0
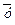 = C1y1(x) + C2y2(x), y1,y2 – частное решение ЛОДУ y” + P1y’ + P2 = 0
= C1y1(x) + C2y2(x), y1,y2 – частное решение ЛОДУ y” + P1y’ + P2 = 0
C1C2 – подбираем так, чтобы они удовлетворяли начальным условиям
 y(x0)=y0 , y’(x0)=y0’, для любых х0
y(x0)=y0 , y’(x0)=y0’, для любых х0  (а,в), и любых y0 ,y0’
(а,в), и любых y0 ,y0’
C1y1(x0) + C2y2(x0) + у*(x0) = y0
C1y’1(x0) + C2y’2(x0) + у*(x0) = y0’
Линейная неоднородная система, определитель этой системы, определитель Вронского
W[y1, y2]≠0 =>система имеет единственное решение при любых 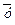 0 ,
0 , 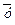 ’0 ,y*0 ,y*’0 , это означает у= у*+
’0 ,y*0 ,y*’0 , это означает у= у*+ 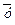 - общее решение ЛНДУ
- общее решение ЛНДУ
Теорема2 принцип суперпозиции (принцип сложения решений)
Если функция yi(x) является решением ЛНДУ
(3) y(n) + P1y(n-1) + … + Pny = fi(x) то функция 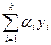 = α1y1 + α2y2 + … + αnyn , то это функция является решением y(n) + P1y(n-1) + … + Pny = α1 f1(x) + α2 f2(x) + … + αn fn(x) (4)
= α1y1 + α2y2 + … + αnyn , то это функция является решением y(n) + P1y(n-1) + … + Pny = α1 f1(x) + α2 f2(x) + … + αn fn(x) (4)
Док-во: для n=2
Подставим y, y’, y”, в (4) , учитываем что y1 y2 решение соответственного уравнения (3)
α1y1” + α2y2” + P1(x)[ α1y1+ α2y2] =
= [α1y1” + P1(x)α1y’1 + P2(x)α1y1] + [α2y2” + P1(x)α2y’2 + P2(x)α2y2] = α1f1(x) + α2f2(x)
56. Линейные неоднородные дифференциальные уравнения n-го порядка с постоянными коэффициентами. Метод неопределенных коэффициентов для уравнений со специальной правой частью. Метод вариации произвольных постоянных (вывод рабочей формулы).
Рассмотрим ЛНДУ с постоянными коэф-ми.
Ур-е у(n) + P1y(n-1) +…+ Pn-1 y’ + Pn y = f(x) : Pi=const
Метод неопр-х коэф-в можно применять если правое ур-е имеет следующий вид: f(x)= 
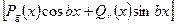 ,
,  ,
, 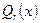 -многочлены степени g и r соотв-но a и b некоторые числа. В основе метода неопр-х коэф-в лежит знание формы частного решения, а именно частное решение стоит искать в аналогич-ой форме свободного члена.
-многочлены степени g и r соотв-но a и b некоторые числа. В основе метода неопр-х коэф-в лежит знание формы частного решения, а именно частное решение стоит искать в аналогич-ой форме свободного члена.
| № | Вид правой части (f(x)) | Корни харак-го уравнения | Вид частного решения y* |
P  (x)=A (x)=A  x x  +A +A  x x  +…
+A +…
+A  x+ A x+ A 
| а) число 0 не явл-ся
корнем хар-го ур-я
б) число 0 явл-ся
корнем хар-го ур-я
кратности 
| а) y*=b  x x  +b +b  x x  +…+
+b +…+
+b  б) y*=x
б) y*=x  (B (B  x x  +B +B  x x  +…
+B +…
+B  ) )
| |
P  (x)e (x)e  = e = e  ( A ( A  x x  +
+A +
+A  x x  +…+A +…+A  x+ A x+ A  )
p-действ-е число )
p-действ-е число
| а) число p не явл-ся
корнем хар-го ур-я
б) число p явл-ся
корнем хар-го ур-я
кратности 
| a) y*= e  ( b ( b  x x  +b +b  x x  +…+
+b +…+
+b  )
б) y*= e )
б) y*= e  x x  ( b ( b  x x  +b +b  x x  +…+
+b +…+
+b  ) )
| |
P  (x)cosgx+Q (x)cosgx+Q  (x)singx
g-число (x)singx
g-число
| а) число 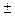 gi-не явл-ся
корнем хар-го ур-я
б) число gi-не явл-ся
корнем хар-го ур-я
б) число 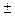 gi-явл-ся
корнем хар-го ур-я
кратности gi-явл-ся
корнем хар-го ур-я
кратности 
| а) y*=  (x)cosgx+ (x)cosgx+  (x)singx
б) y*=x (x)singx
б) y*=x  ( (  (x)cosgx+ (x)cosgx+  (x)singx) (x)singx)
| |
P  (x)e (x)e  cosgx+ Q cosgx+ Q  (x)e (x)e  singx singx
| а) число 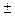 gi-не явл-ся
корнем хар-го ур-я
б) число gi-не явл-ся
корнем хар-го ур-я
б) число 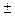 gi-явл-ся
корнем хар-го ур-я
кратности gi-явл-ся
корнем хар-го ур-я
кратности 
| а) y*=  (x) e (x) e  cosgx+ cosgx+  (x)singx
б) y*= x (x)singx
б) y*= x  ( (  (x) e (x) e  cosgx+
+ cosgx+
+  (x)singx) (x)singx)
|
Замечание к таблице: 1)степени многоч-ов P и Q в случаях (3) и (4) можно считать одинаковыми, если они различны, то коэф-ты при недостающих степенях одного из многоч-ов можно считать=0.
2)правая часть ур-я может содержать несколько слагаемых; в этом случае сост-ся из неск-ких слагаемых в соотв-ии с Теоремой о неравенстве нулю вронскиана линейно-независимых решений ЛОДУ
Метод вариации производных постоянных(метод Лагранджа).
Метод позволяет найти решение ДУ независимо от вида правой части, когда известно общее решение соотв-го однородного ДУ.
Например: ДУ 2-го порядка. Пусть y”+P  (x)y’+P
(x)y’+P  (x)y=f(x) (1) пусть y
(x)y=f(x) (1) пусть y  (x) и y
(x) и y  (x)-ФСРЛОДУ
(x)-ФСРЛОДУ
y”+P  (x)y’+P
(x)y’+P  (x)y=0
(x)y=0 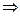
 (x)= C
(x)= C  y
y  (x)+C
(x)+C  y
y  (x) (2). Частное решение y*(x) в виде (14) считая при этом C
(x) (2). Частное решение y*(x) в виде (14) считая при этом C  и C
и C  не постоянными, а неизв-ми функциями от x.
не постоянными, а неизв-ми функциями от x.
y*= C  (x)y
(x)y  (x)+C
(x)+C  (x)y
(x)y  (x), y*= C’
(x), y*= C’  (x)y
(x)y  (x)+C(x)
(x)+C(x)  y’
y’  (x)+C’
(x)+C’  (x)y
(x)y  (x)+ C(x)
(x)+ C(x)  y’
y’  (x)
(x)
Пусть C  (x) и C
(x) и C  (x)
(x) 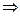 C’
C’  (x)y
(x)y  (x)+ C’
(x)+ C’  (x)y
(x)y  (x)=0 /справедливое равенство (3), тогда y* ’= C
(x)=0 /справедливое равенство (3), тогда y* ’= C  (x)y’
(x)y’  (x)+ C
(x)+ C  (x)y’
(x)y’  (x); y* ”= C
(x); y* ”= C  (x)y’
(x)y’  (x)+ C
(x)+ C  (x)y”
(x)y”  (x)+ C’
(x)+ C’  (x)y’
(x)y’  (x)+ C
(x)+ C  (x)y”
(x)y”  (x).
(x).
Подставим y*, y* ’, y* ” в (1): C  (x)[ y”
(x)[ y”  (x) + P
(x) + P  (x)y
(x)y  ’(x) + P
’(x) + P  (x) y
(x) y  (x)] + C
(x)] + C  (x)[ y”
(x)[ y”  (x) + P
(x) + P  (x)y
(x)y  ’(x) + P
’(x) + P  (x) y
(x) y  (x)] + C’
(x)] + C’  (x)y’
(x)y’  (x)+ C’
(x)+ C’  (x)y’
(x)y’  (x)=f(x). Т.к. y
(x)=f(x). Т.к. y  (x), y
(x), y  (x) решения ОДУ, то выражения []=0
(x) решения ОДУ, то выражения []=0 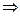 C’
C’  (x)y’
(x)y’  (x) + C’
(x) + C’  (x)y’
(x)y’  (x)=0.
(x)=0.
Объясним два условия и (3):
 |
C’  (x)y
(x)y  (x)+ C’
(x)+ C’  (x)y
(x)y  (x)=0
(x)=0
C’  (x)y’
(x)y’  (x)+ C’
(x)+ C’  (x)y’
(x)y’  (x)=f(x) (4)
(x)=f(x) (4)
Неопр-е ф-ии C’  (x) и C’
(x) и C’  (x).
(x).
Определитель этой системы: W[y  , y
, y  ]=
]= 
 0
0 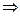 решая систему мы получим C
решая систему мы получим C  (x)=
(x)=  (x),
(x),
C  (x)=
(x)=  (x) проинтегрируем и получим решение
(x) проинтегрируем и получим решение 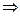 C
C  (x) и C
(x) и C  (x) найдены. Подставим в y*.
(x) найдены. Подставим в y*.
Для ЛНДУ n-го порядка ф-ии C  (x) определяются из системы:
(x) определяются из системы:

C’  (x)y
(x)y  + C’
+ C’  (x)y
(x)y  +…+ C’
+…+ C’ 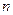 (x)y
(x)y  =0
=0
C’  (x)y’
(x)y’  + C’
+ C’  (x)y’
(x)y’  +…+ C’
+…+ C’ 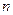 (x)y’
(x)y’  =0
=0
……………………………………………
C’  (x)y
(x)y 
 + C’
+ C’  (x)y
(x)y 
 +…+ C’
+…+ C’ 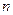 (x)y
(x)y 
 =0
=0
C’  (x)y
(x)y 
 + C’
+ C’  (x)y
(x)y 
 +…+ C’
+…+ C’ 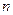 (x)y
(x)y 
 =f(x)
=f(x)
Алгоритм решения ЛНДУ
1) найти ФСР однородного уравнения и записать его общее решение (ОУ)
2) записать частное решение неоднородного ДУ в форме общего решения ОУ считая Ci=Ci (x)
3) построить систему для определения Ci ‘(x) – решить ее
4) найти Ci (x) и подставить их в общее решение НДУ
|
из
5.00
|
Обсуждение в статье: Линейные однородные дифференциальные уравнения n-го порядка с постоянными коэффициентами. Вид частных решений, характеристическое уравнение |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

