Дифференциальные уравнения, сводящиеся к уравнениям с разделяющимися переменными

Копцова Александра Владимировича

Дифференциальные уравнения с разделяющимися переменными.

 

• Среди обыкновенных дифференциальных уравнений первого порядка существуют такие, в которых возможно переменные x и y разнести по разные стороны знака равенства. В уравнениях вида переменные уже разделены, а в ОДУ 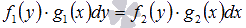переменные разделяются посредством преобразований. Кроме того, некоторые дифференциальные уравнения сводятся к уравнениям с разделяющимися переменными после введения новых переменных.
  
  
  
  
  

Дифференциальные уравнения с разделенными переменными .

Дифференциальные уравнения называют уравнениями с разделенными переменными.

Название этого вида дифференциальных уравнений достаточно показательно: выражения, содержащие переменные x и y, разделены знаком равенства, то есть, находятся по разные стороны от него.

Будем считать, что функции f(y) и g(x) непрерывны.

Общим интегралом уравнения с разделенными переменными является равенство . Если интегралы из этого равенства выражаются в элементарных функциях, то мы можем получить общее решение дифференциального уравнения как неявно заданную функцию Ф(x, y) = 0, а иногда получается выразить функцию y в явном виде.

Пример.

Найдите общее решение дифференциального уравнения с разделенными переменными .

Решение.

Проинтегрируем обе части равенства: . По сути, мы уже получили общее решение исходного дифференциального уравнения, так как свели задачу решения дифференциального уравнения к уже известной задаче нахождения неопределенных интегралов. Однако, эти неопределенные интегралы выражаются в элементарных функциях, и мы можем взять их, используя таблицу первообразных:

где С₁ и С₂ – произвольные постоянные.

Мы пришли к неявно заданной функции , которая является общим решением исходного дифференциального уравнения с разделенными переменными. Ответ можно оставить в таком виде. Но в нашем случае искомую функцию y можно выразить явно через аргумент x. Итак, , где . То есть, функция является общим решением исходного дифференциального уравнения.

Замечание.

Ответ можно записать в любом из трех видов или , или .

Дифференциальные уравнения с разделяющимися переменными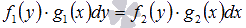

Прежде чем продолжить, напомним, что 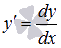когда y является функцией аргумента x.

В дифференциальных уравнениях 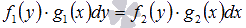или переменные могут быть разделены, проведением преобразований. Такие ОДУ называются дифференциальными уравнениями с разделяющимися переменными. Соответствующее ДУ с разделенными переменными запишется как .

Пример.

Найти все решения дифференциального уравнения .

Решение.

Это уравнение с разделяющимися переменными, так как мы можем разделить x и y:

Для нулевой функции y исходное уравнение обращается в тождество , поэтому, y = 0 является решением дифференциального уравнения. Это решение мы могли упустить из виду.

Проинтегрируем дифференциальное уравнение с разделенными переменными :

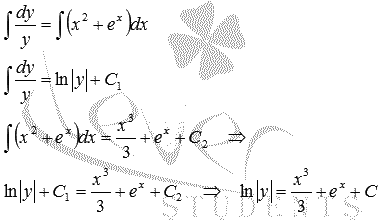
В преобразованиях мы заменили C₂ - C₁ на С.

Мы получили решение ДУ в виде неявно заданной функции . На этом можно закончить. Однако в нашем случае функцию y можно выразить явно, проведя потенцирование полученного равенства:

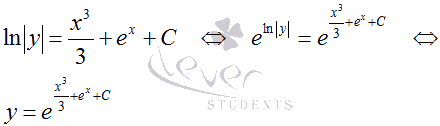
Ответ: .

Дифференциальные уравнения, сводящиеся к уравнениям с разделяющимися переменными , a ≠ 0, b ≠ 0

Обыкновенные дифференциальные уравнения первого порядка вида , a ≠ 0,

b ≠ 0 приводятся к уравнениям с разделяющимися переменными введением новой переменной z = ax + by, где z представляет собой функцию аргумента x.

В этом случае

После подстановки в исходное уравнение и небольших преобразований приходим к уравнению с разделенными переменными

Рассмотрим пример.

Пример.
Найдите общее решение дифференциального уравнения и частное решение, удовлетворяющее начальному условию y(0) = e.

Решение.

Пусть z = 2x + y, тогда

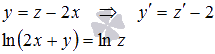
Подставим полученные результаты в исходное уравнение и преобразуем его к дифференциальному уравнению с разделяющимися переменными:

Разделяем переменные и интегрируем обе части равенства 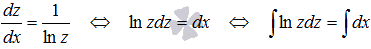. Интеграл в левой части найдем методом интегрирования по частям, а интеграл в правой части является табличным:

Следовательно, . Если принять C = C₂ - C₁ и сделать обратную замену z = 2x + y, то получим общее решение дифференциального уравнения в виде неявно заданной функции: .

Осталось найти частное решение, удовлетворяющее начальному условию y(0) = e. Для этого подставляем x = 0 и y(0) = e в общее решение дифференциального уравнения и находим значение константы С:

Следовательно, искомое частное решение, удовлетворяющее условию y(0) = e, имеет вид .

Замечание.

В условии задачи ничего не сказано об интервале, на котором требуется найти общее решение дифференциального уравнения. В таких случаях решение проводится для всех значений аргумента x, при которых исходное дифференциальное уравнение и его решения имеют смысл. Для данного примера дифференциальное уравнение имеет смысл при .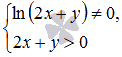

 

Дифференциальные уравнения, сводящиеся к уравнениям с разделяющимися переменными или .

Дифференциальные уравнения вида или могут быть сведены к ОДУ с разделяющимися переменными, если произвести замену или 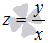, где z – функция аргумента x.

Если , то и по правилу дифференцирования дроби 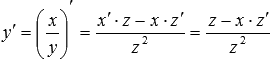. В этом случае уравнения примут вид или .

Если принять 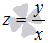, то y = x ⋅ z и по правилу производной произведения . В этому случае уравнения сведутся к или .

Пример.
Решите дифференциальное уравнение .

Решение.

Примем 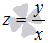, тогда 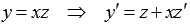. Подставим в исходное уравнение:

Получили уравнение с разделенными переменными. Проинтегрируем его.

После обратной замены получаем общее решение исходного дифференциального уравнения в виде неявно заданной функции .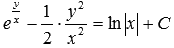

Следует остановиться на дифференциальных уравнениях вида

.

Делением числителя и знаменателя правой части на yⁿ или xⁿ такие дифференциальные уравнения приводятся к виду или .

Пример.

Найти общее решение дифференциального уравнения .

Решение.

В этом примере x и y отличны от нуля. Разделим и числитель и знаменатель правой части равенства наx²:

Введем новую переменную 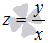, тогда .

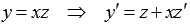Подставляем в исходное уравнение

Получили дифференциальное уравнение с разделенными переменными. Решаем его

В этом примере можно получить решение и в явном виде. Для этого примем и воспользуемся свойствами логарифма:

Осталось сделать обратную замену y = x ⋅ z и записать ответ . Это общее решение дифференциального уравнения.

Замечание: это уравнение (как и другие подобного типа) можно решить и используя замену .

Опишем решение для этой замены.

Разделим и числитель и знаменатель на y²:

Пусть , тогда .

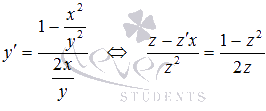Подставляем все в исходное уравнение и получаем дифференциальное уравнение с разделяющимися переменными . После разделения переменных приходим к равенству . Интегрируем его

Возьмем сначала интеграл . После разложения на простейшие дроби подынтегральной функции интеграл примет вид . Теперь проведем интегрирование простейших дробей:

Теперь найдем интеграл :

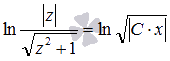В итоге имеем или , где .

После проведения обратной замены и некоторых преобразований придем к тому же результату .

Сделаем вывод. В этом примере при замене решение оказалось более трудоемким, чем при замене 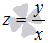. Для себя можно отметить, что если решение дифференциального уравнения или оказывается сложным при выбранной замене , то можно попробовать ввести другую переменную, то есть .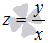

 

Дифференциальные уравнения, сводящиеся к уравнениям с разделяющимися переменными .

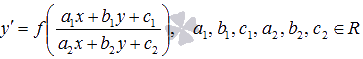
Дифференциальные уравнения можно свести к уравнениям или , следовательно, к уравнениям с разделяющимися переменными. Для этого находится (x₀ , y₀) - решение системы двух линейных однородных уравнений и вводятся новые переменные . После такой замены уравнение примет вид .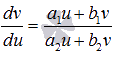

Разберемся на примере.

Пример.

Найти общее решение дифференциального уравнения .

Решение.

Составляем и решаем систему линейных уравнений

Делаем замену переменных

После подстановки в исходное уравнение получаем . После деления на u числителя и знаменателя правой части имеем .

Вводим новую переменную , тогда

Возвращаемся к исходным переменным, производя обратную замену :

Это есть общее решение дифференциального уравнения.